1643-第 K 条最小指令

Bob 站在单元格 (0, 0) ，想要前往目的地 destination ：(row, column) 。他只能向 右 或向
下 走。你可以为 Bob 提供导航 指令 来帮助他到达目的地 destination 。

指令 用字符串表示，其中每个字符：

• 'H' ，意味着水平向右移动
• 'V' ，意味着竖直向下移动

能够为 Bob 导航到目的地 destination 的指令可以有多种，例如，如果目的地 destination 是 (2, 3)，"HHHVV" 和 "HVHVH" 都是有效 指令 。

然而，Bob 很挑剔。因为他的幸运数字是 k，他想要遵循 **按字典序排列后的第k 条最小指令 **的导航前往目的地 destination
。k 的编号 从 1 开始 。

给你一个整数数组 destination 和一个整数 k ，请你返回可以为 __ Bob __ 提供前往目的地 destination 导航的
**按字典序排列后的第k 条最小指令 **。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/11/01/ex1.png)

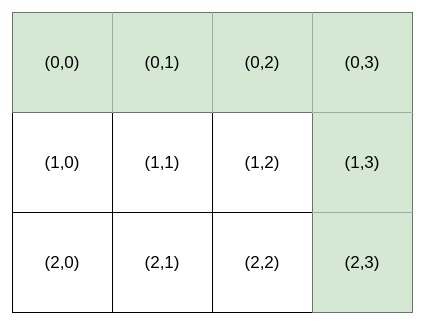
**输入：** destination = [2,3], k = 1
**输出：** "HHHVV"
**解释：** 能前往 (2, 3) 的所有导航指令 **按字典序排列后** 如下所示：
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH", "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"].

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/11/01/ex2.png)

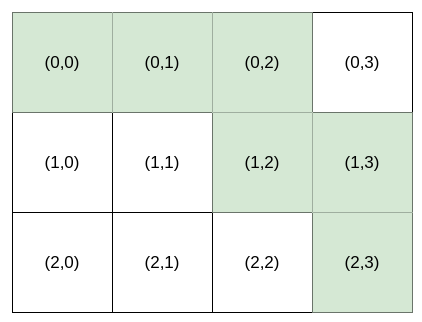
**输入：** destination = [2,3], k = 2
**输出：** "HHVHV"

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/11/01/ex3.png)

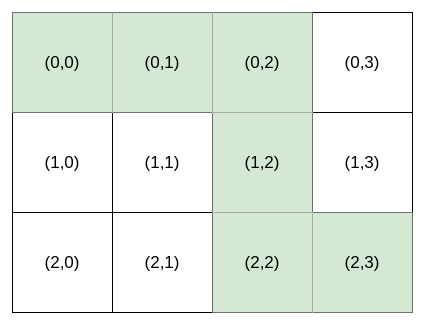
**输入：** destination = [2,3], k = 3
**输出：** "HHVVH"

提示：

• destination.length == 2
• 1 <= row, column <= 15
• 1 <= k <= nCr(row + column, row)，其中 nCr(a, b) 表示组合数，即从 a 个物品中选 b 个物品的不同方案数。

问题分析

初步分析：

• 问题目标： 求合法的导航指令按字典序排列后的第 k 条指令；
• 问题要件： 对于从 [0, 0] 到 [r,c] 的合法导航指令中，有且仅有 r 个 V 指令与 c 个 H 指令
• 问题抽象： 因此，原问题相当于求 r 个 V 指令与 c 个 H 指令 [HHH..VVV] 的「第 k 个排列」：

对于「第 k 个排列问题」，可以先解决 LeetCode 经典题 60. 排列序列 ，核心思想是优先确定高位元素，通过子树规模与 k 的对比直接定位第 k 个排列存在的子树

区别在于：

第 k 个排列问题是全排列问题，即每一个节点的子树都是规模为 (n - 1)! 的问题，而这道题中选择列表有重复数，因此总方案数为 C_{h+v}^h，问题目标是求第 k 个排列数。

C_{h+v}^h 表示在 h + v 个位置中选择 h 个位置放置 H，剩余的位置放置 V。

具体实现：

• 定义问题： 定义 (h, v, k) 表示在 h 个 H 指令与 v 个 V 指令的第 k 个排列问题；
• 分类讨论：
  • 由于 H < V，左子树表示选择 H，右子树表示选择 V：
  • 左子树的规模为 cnt1 = C_{h+v-1}^{h - 1
  • 右子树的规模为 cnt2 = C_{h+v-1}^{h
  • 如果 k <= cnt1，说明目标方案在左子树；
  • 如果 k > cnt1，说明目标方案在右子树；
• 预处理： 算法中需要计算组合数，可以预处理 C_{h+v}^0 到 C_{h+v}^h 的组合数。

class Solution {

    companion object {
        // 预处理组合数
        val H = 15
        val comb = Array(H * 2 + 1) { IntArray(H + 1) }
        init {
            comb[0][0] = 1
            for (i in 1 .. H * 2) {
                comb[i][0] = 1
                for (j in 1 .. min(i, H)) {
                    comb[i][j] = comb[i - 1][j - 1] + comb[i - 1][j]
                }
            }
        }
    }

    fun kthSmallestPath(d: IntArray, k_: Int): String {
        var v = d[0]
        var h = d[1]
        var k = k_
        val ret = StringBuilder()
        repeat(h + v) {
            // println("h=h, v=v, k=k")
            if (h <= 0) {
                ret.append("V")
                v--
                return@repeat
            }
            val cnt1 = comb[h + v - 1][h - 1]
            if (k <= cnt1) {
                ret.append("H")
                h--
            } else {
                ret.append("V")
                v--
                k -= cnt1 // 剪枝
            }
        }
        return ret.toString()
    }
}

复杂度分析：

• 时间复杂度：O(h+v) 每位字符的计算时间为 O(1)；
• 空间复杂度：O(C_{h+v-1}^h) 预处理组合数空间。