1719-重构一棵树的方案数

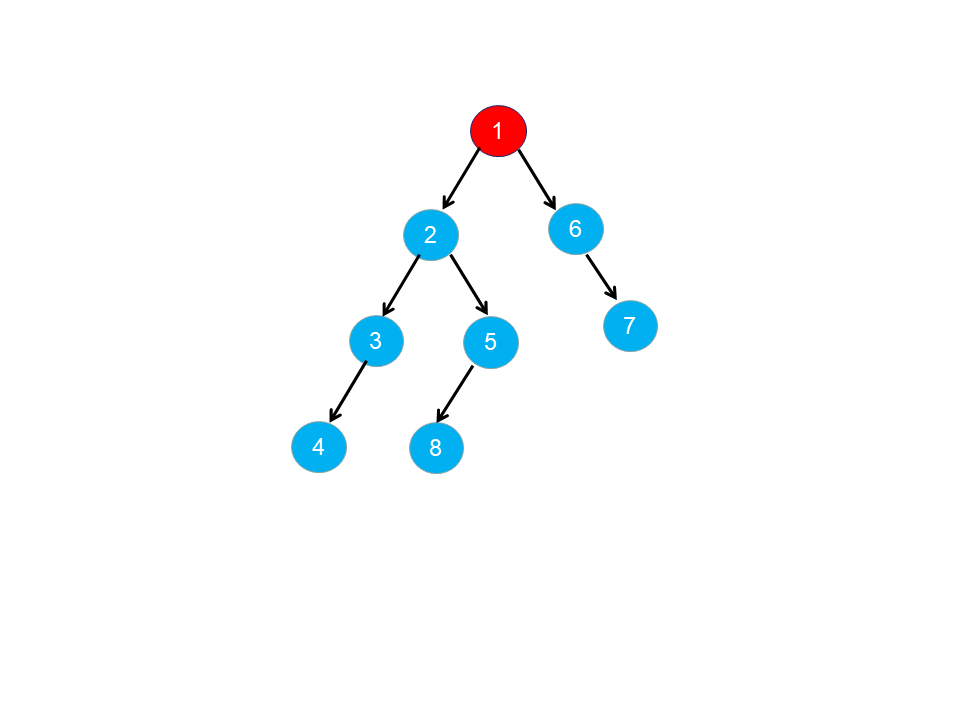
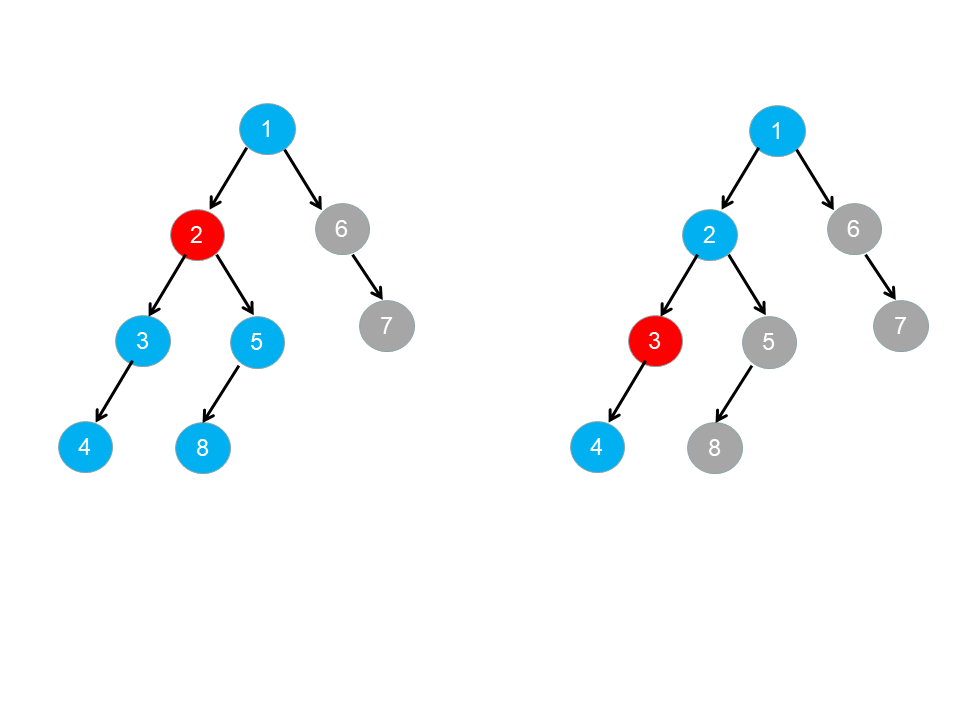
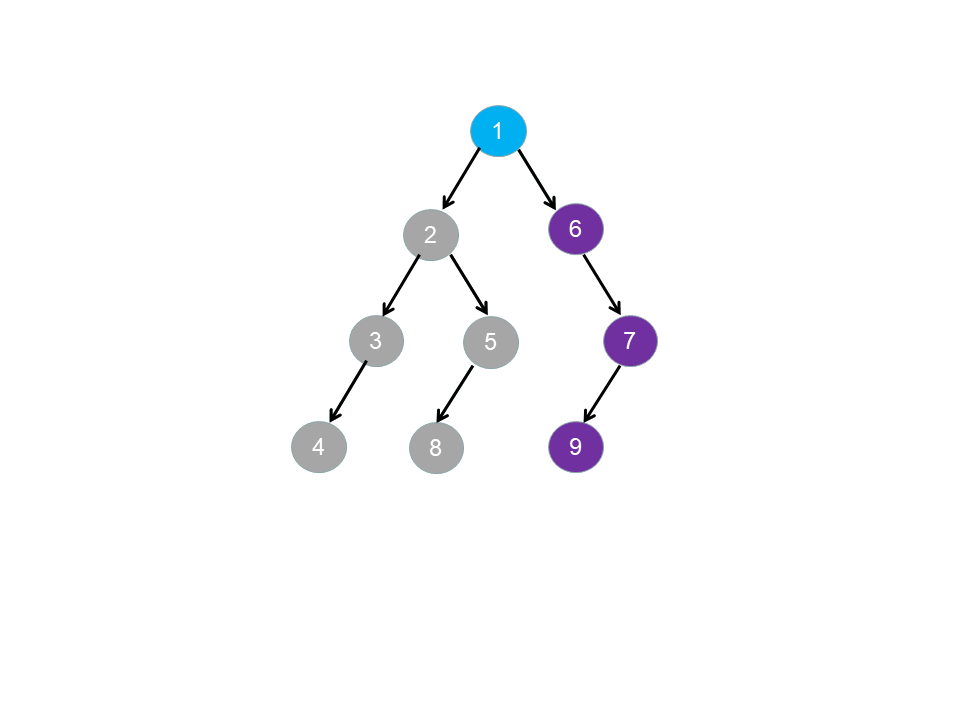
给你一个数组 pairs ，其中 pairs[i] = [xi, yi] ，并且满足：

• pairs 中没有重复元素
• xi < yi

令 ways 为满足下面条件的有根树的方案数：

• 树所包含的所有节点值都在 pairs 中。
• 一个数对 [xi, yi] 出现在 pairs 中 当且仅当 ****xi 是 yi 的祖先或者 yi 是 xi 的祖先。
• 注意： 构造出来的树不一定是二叉树。

两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。

请你返回：

• 如果 ways == 0 ，返回 0 。
• 如果 ways == 1 ，返回 1 。
• 如果 ways > 1 ，返回 2 。

一棵 有根树 指的是只有一个根节点的树，所有边都是从根往外的方向。

我们称从根到一个节点路径上的任意一个节点（除去节点本身）都是该节点的 祖先 。根节点没有祖先。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/01/09/trees2.png)

**输入：** pairs = [[1,2],[2,3]]
**输出：** 1
**解释：** 如上图所示，有且只有一个符合规定的有根树。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/01/09/tree.png)

**输入：** pairs = [[1,2],[2,3],[1,3]]
**输出：** 2
**解释：** 有多个符合规定的有根树，其中三个如上图所示。

示例 3：

**输入：** pairs = [[1,2],[2,3],[2,4],[1,5]]
**输出：** 0
**解释：** 没有符合规定的有根树。

提示：

• 1 <= pairs.length <= 105
• 1 <= xi < yi <= 500
• pairs 中的元素互不相同。

方法一：直接模拟

思路

本题抽象思维难度较大，需要仔细考虑树的结构。题目给定的数对 pairs}[i] = [x_{i},y_{i}]，且满足 x_{i 是 y_{i 的祖先或者 y_{i 是 x_{i 的祖先；树中所包含的所有节点值都在 pairs 中，即 pairs 包含树中所有可能构成祖先的数对。

设树中节点数目为 n，pairs 中包含节点 x 的数对的数目为 degree}[x]，节点 x 的祖先和后代的节点集合为 adj}[x]。

下面来研究 degree 的性质。

• 根节点为树中其余所有节点的祖先，根节点与其余所有节点都能构成数对。设根节点为 root，由于 pairs 包含树中所有可能构成祖先的数对，因此 degree}[\textit{root}] = n - 1。如下图所示，根节点 1 为其余节点的祖先，蓝色节点组成了 adj}[1]。

• 对于 pairs 中的数对 [x_{i},y_{i}]，如果 x_{i 为 y_{i 的祖先，则一定满足 degree}[x_{i}] \ge \textit{degree}[y_{i}]。如果节点 y_j 为节点 y_{i 的后代节点，则节点 y_j 一定同时也是节点 x_{i 的后代节点；如果节点 y_j 为节点 y_{i 的祖先节点，则节点 y_j 要么是节点 x_{i 的祖先节点，要么是节点 x_{i 的后代节点，所以一定满足 degree}[x_{i}] \ge \textit{degree}[y_{i}]。此外，如果 x_{i 为 y_{i 的祖先，则一定满足 adj}[y_{i}] \in \textit{adj}[x_{i}]。如下图所示，含有节点 2 的数对数目一定大于含有节点 3 的数对数目。

• 对于 pairs 中的数对 [x_{i},y_{i}]，如果 x_{i 为 y_{i 的祖先，且满足 degree}[x_{i}] = \textit{degree}[y_{i}] 和 adj[x_{i}] = adj[y_{i}]，则 x_{i 到 y_{i 途径的所有节点均只有一个孩子节点。此时 x_{i 到 y_{i 之间的节点包含的数对关系是一样的，x_{i 到 y_{i 之间的节点是可以进行互相交换而不影响树的结构，则此时构成树的方案数一定不是唯一的。如下图所示，节点 6,7,9 满足上述要求：

综上所述，对于 pairs 中的数对 [x_{i},y_{i}]：

• 若 degree}[x_{i}] > \textit{degree}[y_{i}]，则 x_{i 为 y_{i 的祖先节点；
• 若 degree}[x_{i}] < \textit{degree}[y_{i}]，则 y_{i 为 x_{i 的祖先节点；
• 若 degree}[x_{i}] = \textit{degree}[y_{i}]，则可能存在多种构造方法，y_{i 为 x_{i 的祖先或者 x_{i 为 y_{i 的祖先。

通过以上分析结论，我们可以尝试进行重新建树，并检查建成的树是否合法。

• 首先我们需要找到根节点 root，通过上述结论，我们找到满足 degree}[\textit{root}] = n - 1 的节点，如果不存在根节点，则认为其不能构成合法的树，返回 0。

• 我们需要利用上述的结论检测是构建的树是否合法，遍历每个节点 node}_i，找到 node}i 的祖先 parent}{i，检测集合 adj}[\textit{node}_i] 是否为 adj}[\textit{\textit{parent} }_i] 的子集。可以利用 degree}[\textit{node}i] \le \textit{degree}[\textit{parent}{i}] 找到所有属于 node}_i 的祖先节点，然后依次检测是否满足 adj}[\textit{node}_i] \in \textit{adj}[\textit{\textit{parent} }_i]，如果不满足要求，则认为构建的树为非法，返回 0。

• 实际检测过程中不必检测节点 node}_i 的所有祖先节点，只需要检测节点 node}_i 的父节点是否满足子集包含的要求即可。根据上述推论找到节点 x 满足 degree}[x] 最小且 degree}[x] \ge \textit{degree}[\textit{node}_i]，则此时找到的节点为节点 node}_i 的父亲节点，此时只需检测父亲节点是否满足上述要求即可。

• 设 node}_i 的父节点为 parent，若满足 degree}[\textit{node}_i] = \textit{degree}[\textit{parent}] 则树的构造方式可以有多个，返回 2。

代码

[sol1-Python3]

class Solution:
    def checkWays(self, pairs: List[List[int]]) -> int:
        adj = defaultdict(set)
        for x, y in pairs:
            adj[x].add(y)
            adj[y].add(x)

        # 检测是否存在根节点
        root = next((node for node, neighbours in adj.items() if len(neighbours) == len(adj) - 1), -1)
        if root == -1:
            return 0

        ans = 1
        for node, neighbours in adj.items():
            if node == root:
                continue

            currDegree = len(neighbours)
            parent = -1
            parentDegree = maxsize
            # 根据 degree 的大小找到 node 的父节点 parent
            for neighbour in neighbours:
                if currDegree <= len(adj[neighbour]) < parentDegree:
                    parent = neighbour
                    parentDegree = len(adj[neighbour])
            # 检测 neighbours 是否为 adj[parent] 的子集
            if parent == -1 or any(neighbour != parent and neighbour not in adj[parent] for neighbour in neighbours):
                return 0

            if parentDegree == currDegree:
                ans = 2
        return ans

[sol1-C++]

class Solution {
public:
    int checkWays(vector<vector<int>>& pairs) {
        unordered_map<int, unordered_set<int>> adj;
        for (auto &p : pairs) {
            adj[p[0]].emplace(p[1]);
            adj[p[1]].emplace(p[0]);
        }
        /* 检测是否存在根节点*/
        int root = -1;
        for (auto &[node, neighbours] : adj) {
            if (neighbours.size() == adj.size() - 1) {
                root = node;
                break;
            }
        }
        if (root == -1) {
            return 0;
        }

        int res = 1;
        for (auto &[node, neighbours] : adj) {
            if (node == root) {
                continue;
            }
            int currDegree = neighbours.size();
            int parent = -1;
            int parentDegree = INT_MAX;

            /* 根据 degree 的大小找到 node 的父节点 parent */
            for (auto &neighbour : neighbours) {
                if (adj[neighbour].size() < parentDegree && adj[neighbour].size() >= currDegree) {
                    parent = neighbour;
                    parentDegree = adj[neighbour].size();
                }
            }
            if (parent == -1) {
                return 0;
            }

            /* 检测 neighbours 是否是 adj[parent] 的子集 */
            for (auto &neighbour : neighbours) {
                if (neighbour == parent) {
                    continue;
                }
                if (!adj[parent].count(neighbour)) {
                    return 0;
                }
            }
            if (parentDegree == currDegree) {
                res = 2;
            }
        }
        return res;
    }
};

[sol1-Java]

class Solution {
    public int checkWays(int[][] pairs) {
        Map<Integer, Set<Integer>> adj = new HashMap<Integer, Set<Integer>>();
        for (int[] p : pairs) {
            adj.putIfAbsent(p[0], new HashSet<Integer>());
            adj.putIfAbsent(p[1], new HashSet<Integer>());
            adj.get(p[0]).add(p[1]);
            adj.get(p[1]).add(p[0]);
        }
        /* 检测是否存在根节点*/
        int root = -1;
        Set<Map.Entry<Integer, Set<Integer>>> entries = adj.entrySet();
        for (Map.Entry<Integer, Set<Integer>> entry : entries) {
            int node = entry.getKey();
            Set<Integer> neighbours = entry.getValue();
            if (neighbours.size() == adj.size() - 1) {
                root = node;
            }
        }
        if (root == -1) {
            return 0;
        }

        int res = 1;
        for (Map.Entry<Integer, Set<Integer>> entry : entries) {
            int node = entry.getKey();
            Set<Integer> neighbours = entry.getValue();
            if (node == root) {
                continue;
            }
            int currDegree = neighbours.size();
            int parent = -1;
            int parentDegree = Integer.MAX_VALUE;

            /* 根据 degree 的大小找到 node 的父节点 parent */
            for (int neighbour : neighbours) {
                if (adj.get(neighbour).size() < parentDegree && adj.get(neighbour).size() >= currDegree) {
                    parent = neighbour;
                    parentDegree = adj.get(neighbour).size();
                }
            }
            if (parent == -1) {
                return 0;
            }

            /* 检测 neighbours 是否是 adj[parent] 的子集 */
            for (int neighbour : neighbours) {
                if (neighbour == parent) {
                    continue;
                }
                if (!adj.get(parent).contains(neighbour)) {
                    return 0;
                }
            }
            if (parentDegree == currDegree) {
                res = 2;
            }
        }
        return res;
    }
}

[sol1-C#]

public class Solution {
    public int CheckWays(int[][] pairs) {
        Dictionary<int, ISet<int>> adj = new Dictionary<int, ISet<int>>();
        foreach (int[] p in pairs) {
            if (!adj.ContainsKey(p[0])) {
                adj.Add(p[0], new HashSet<int>());
            }
            if (!adj.ContainsKey(p[1])) {
                adj.Add(p[1], new HashSet<int>());
            }
            adj[p[0]].Add(p[1]);
            adj[p[1]].Add(p[0]);
        }
        /* 检测是否存在根节点*/
        int root = -1;
        foreach (KeyValuePair<int, ISet<int>> pair in adj) {
            int node = pair.Key;
            ISet<int> neighbours = pair.Value;
            if (neighbours.Count == adj.Count - 1) {
                root = node;
            }
        }
        if (root == -1) {
            return 0;
        }

        int res = 1;
        foreach (KeyValuePair<int, ISet<int>> pair in adj) {
            int node = pair.Key;
            ISet<int> neighbours = pair.Value;
            /* 如果当前节点为根节点 */
            if (node == root) {
                continue;
            }
            int currDegree = neighbours.Count;
            int parent = -1;
            int parentDegree = int.MaxValue;

            /* 根据 degree 的大小找到 node 的父节点 parent */
            foreach (int neighbour in neighbours) {
                if (adj[neighbour].Count < parentDegree && adj[neighbour].Count >= currDegree) {
                    parent = neighbour;
                    parentDegree = adj[neighbour].Count;
                }
            }
            if (parent == -1) {
                return 0;
            }

            /* 检测父节点的集合是否包含所有的孩子节点 */
            foreach (int neighbour in neighbours) {
                if (neighbour == parent) {
                    continue;
                }
                if (!adj[parent].Contains(neighbour)) {
                    return 0;
                }
            }
            if (parentDegree == currDegree) {
                res = 2;
            }
        }
        return res;
    }
}

[sol1-C]

typedef struct {
    int key;
    UT_hash_handle hh;
} HashEntry;

void hashInsert(HashEntry ** obj, int key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(int), pEntry);
    if (NULL == pEntry) {
        pEntry = (HashEntry *)malloc(sizeof(HashEntry));
        pEntry->key = key;
        HASH_ADD(hh, *obj, key, sizeof(int), pEntry);
    }
}

bool hashFind(HashEntry ** obj, int key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(int), pEntry);
    if (NULL == pEntry) {
        return false;
    } else {
        return true;
    }
}

void hashFreeAll(HashEntry ** obj) {
    HashEntry *curr, *next;
    HASH_ITER(hh, *obj, curr, next) {
        HASH_DEL(*obj, curr);  
        free(curr);
    }
}

#define MAX_NODE_SIZE 501

int checkWays(int** pairs, int pairsSize, int* pairsColSize) {
    HashEntry * adj[MAX_NODE_SIZE];
    memset(adj, 0, sizeof(HashEntry *) * MAX_NODE_SIZE);
    for (int i = 0; i < pairsSize; i++) {
        hashInsert(&adj[pairs[i][0]], pairs[i][1]);
        hashInsert(&adj[pairs[i][1]], pairs[i][0]);
    }
    int nodeSize = 0;
    for (int i = 0; i < MAX_NODE_SIZE; i++) {
        if (NULL != adj[i]) {
            nodeSize++;
        }
    }
    /* 检测是否存在根节点*/
    int root = -1;
    for (int i = 0; i < MAX_NODE_SIZE; i++) {
        unsigned int degree = HASH_COUNT(adj[i]);
        if (degree == nodeSize - 1) {
            root = i;
            break;
        }
    }
    if (root == -1) {
        return 0;
    }

    int res = 1;
    for (int i = 0; i < MAX_NODE_SIZE; i++) {
        if (root == i || NULL == adj[i]) {
            continue;
        }
        int currDegree = HASH_COUNT(adj[i]);
        int parent = -1;
        int parentDegree = INT_MAX;

        /* 根据 degree 的大小找到当前节点的父节点 */
        HashEntry *curr = NULL, *next = NULL;
        HASH_ITER(hh, adj[i], curr, next) {
            if (HASH_COUNT(adj[curr->key]) < parentDegree && HASH_COUNT(adj[curr->key]) >= currDegree) {
                parent = curr->key;
                parentDegree = HASH_COUNT(adj[curr->key]);
            }
        }
        if (parent == -1) {
            return 0;
        }
        
        /* 检测 adj[node] 是否是 adj[parent] 的子集 */
        HASH_ITER(hh, adj[i], curr, next) {
            if (curr->key == parent) {
                continue;
            }
            if (!hashFind(&adj[parent], curr->key)) {
                return 0;
            }
        }
        if (parentDegree == currDegree) {
            res = 2;
        }
    }
    for (int i = 0; i < MAX_NODE_SIZE; i++) {
        hashFreeAll(&adj[i]);
    }
    return res;
}

[sol1-JavaScript]

var checkWays = function(pairs) {
    const adj = new Map();
    for (const p of pairs) {
        if (!adj.has(p[0])) {
            adj.set(p[0], new Set());
        }
        if (!adj.has(p[1])) {
            adj.set(p[1], new Set());
        }
        adj.get(p[0]).add(p[1]);
        adj.get(p[1]).add(p[0]);
    }
    /* 检测是否存在根节点*/
    let root = -1;
    const entries = new Set();
    for (const entry of adj.entries()) {
        entries.add(entry);
    }
    for (const [node, neg] of entries) {
        if (neg.size === adj.size - 1) {
            root = node;
        }
    }
    if (root === -1) {
        return 0;
    }
    let res = 1;
    for (const [node, neg] of entries) {
        /* 如果当前节点为根节点 */
        if (root === node) {
            continue;
        }
        const currDegree = neg.size;
        let parentNode = -1;
        let parentDegree = Number.MAX_SAFE_INTEGER;
        /* 根据degree的大小找到当前节点的父节点 */
        for (const neighbour of neg) {
            if (adj.has(neighbour) && adj.get(neighbour).size < parentDegree && adj.get(neighbour).size >= currDegree) {
                parentNode = neighbour;
                parentDegree = adj.get(neighbour).size;
            }
        }
        if (parentNode === -1) {
            return 0;
        }
        /* 检测父节点的集合是否包含所有的孩子节点 */
        for (const neighbour of neg) {
            if (neighbour === parentNode) {
                continue;
            }
            if (!adj.get(parentNode).has(neighbour)) {
                return 0;
            }
        }
        if (parentDegree === currDegree) {
            res = 2;
        }
    }
    return res;
};

[sol1-Golang]

func checkWays(pairs [][]int) int {
    adj := map[int]map[int]bool{}
    for _, p := range pairs {
        x, y := p[0], p[1]
        if adj[x] == nil {
            adj[x] = map[int]bool{}
        }
        adj[x][y] = true
        if adj[y] == nil {
            adj[y] = map[int]bool{}
        }
        adj[y][x] = true
    }

    // 检测是否存在根节点
    root := -1
    for node, neighbours := range adj {
        if len(neighbours) == len(adj)-1 {
            root = node
            break
        }
    }
    if root == -1 {
        return 0
    }

    ans := 1
    for node, neighbours := range adj {
        if node == root {
            continue
        }

        currDegree := len(neighbours)
        parent := -1
        parentDegree := math.MaxInt32
        // 根据 degree 的大小找到 node 的父节点 parent
        for neighbour := range neighbours {
            if len(adj[neighbour]) < parentDegree && len(adj[neighbour]) >= currDegree {
                parent = neighbour
                parentDegree = len(adj[neighbour])
            }
        }
        if parent == -1 {
            return 0
        }
        // 检测 neighbours 是否为 adj[parent] 的子集
        for neighbour := range neighbours {
            if neighbour != parent && !adj[parent][neighbour] {
                return 0
            }
        }

        if parentDegree == currDegree {
            ans = 2
        }
    }
    return ans
}

复杂度分析

• 时间复杂度：O(m + n^2)，其中 n 为树中节点的数目，m 表示数组 pairs 的长度。需要遍历 pairs ，时间复杂度为 O(m)，然后遍历所有的节点，检测每个节点的父节点对应的集合是否包含当前节点的对应的集合，集合中最多有 n 个元素，时间复杂度为 O(n^2)，因此总的时间复杂度为 O(m + n^2)。

• 空间复杂度：O(m)，m 表示数组 pairs 的长度。需要 O(m) 的空间来存储节点对应的集合关系。