1728-猫和老鼠 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

一只猫和一只老鼠在玩一个叫做猫和老鼠的游戏。

它们所处的环境设定是一个 rows x cols 的方格 grid ，其中每个格子可能是一堵墙、一块地板、一位玩家（猫或者老鼠）或者食物。

  • 玩家由字符 'C' （代表猫）和 'M' （代表老鼠）表示。
  • 地板由字符 '.' 表示，玩家可以通过这个格子。
  • 墙用字符 '#' 表示，玩家不能通过这个格子。
  • 食物用字符 'F' 表示，玩家可以通过这个格子。
  • 字符 'C' ， 'M' 和 'F' 在 grid 中都只会出现一次。

猫和老鼠按照如下规则移动：

  • 老鼠 先移动 ，然后两名玩家轮流移动。
  • 每一次操作时，猫和老鼠可以跳到上下左右四个方向之一的格子，他们不能跳过墙也不能跳出 grid 。
  • catJump 和 mouseJump 是猫和老鼠分别跳一次能到达的最远距离，它们也可以跳小于最大距离的长度。
  • 它们可以停留在原地。
  • 老鼠可以跳跃过猫的位置。

游戏有 4 种方式会结束：

  • 如果猫跟老鼠处在相同的位置，那么猫获胜。
  • 如果猫先到达食物，那么猫获胜。
  • 如果老鼠先到达食物，那么老鼠获胜。
  • 如果老鼠不能在 1000 次操作以内到达食物，那么猫获胜。

给你 rows x cols 的矩阵 grid 和两个整数 catJump 和 mouseJump
，双方都采取最优策略，如果老鼠获胜，那么请你返回 true ，否则返回 false 。

示例 1：

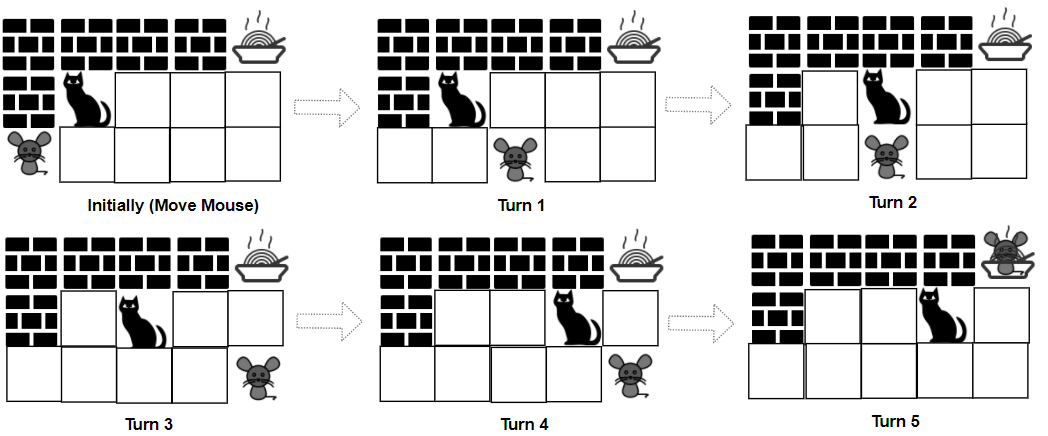
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/01/17/sample_111_1955.png)

**输入：** grid = ["####F","#C...","M...."], catJump = 1, mouseJump = 2
**输出：** true
**解释：** 猫无法抓到老鼠，也没法比老鼠先到达食物。

示例 2：

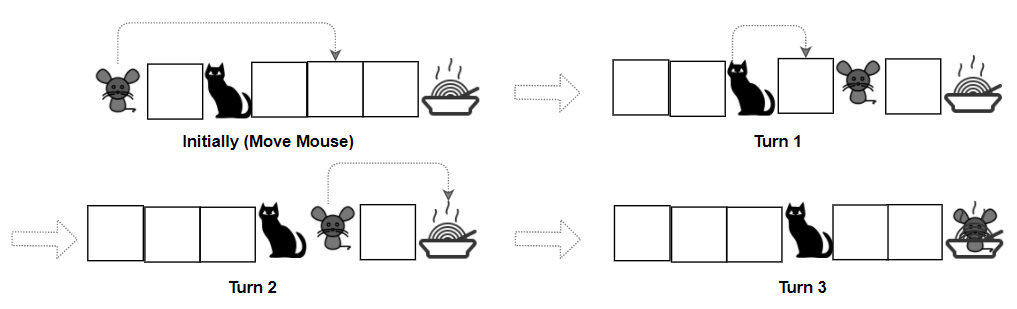
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/01/17/sample_2_1955.png)

**输入：** grid = ["M.C...F"], catJump = 1, mouseJump = 4
**输出：** true

示例 3：

**输入：** grid = ["M.C...F"], catJump = 1, mouseJump = 3
**输出：** false

示例 4：

**输入：** grid = ["C...#","...#F","....#","M...."], catJump = 2, mouseJump = 5
**输出：** false

示例 5：

**输入：** grid = [".M...","..#..","#..#.","C#.#.","...#F"], catJump = 3, mouseJump = 1
**输出：** true

提示：

  • rows == grid.length
  • cols = grid[i].length
  • 1 <= rows, cols <= 8
  • grid[i][j] 只包含字符 'C' ，'M' ，'F' ，'.' 和 '#' 。
  • grid 中只包含一个 'C' ，'M' 和 'F' 。
  • 1 <= catJump, mouseJump <= 8

前言

这道题是「913. 猫和老鼠 」的进阶，建议读者在阅读本文之前首先阅读「913. 猫和老鼠的官方题解 」，了解博弈问题中的必胜状态、必败状态与必和状态的概念，以及最优策略。

博弈问题通常可以使用动态规划求解。由于动态规划的时间复杂度和游戏轮数有关，因此动态规划的时间复杂度较高。本文不具体介绍动态规划的解法，感兴趣的读者可以自行尝试。

博弈问题的另一种解法是拓扑排序。和动态规划相比，拓扑排序的时间复杂度和游戏轮数无关，因此拓扑排序的时间复杂度较低。

方法一：拓扑排序

概述

给定的网格包含 rows 行和 cols 列，网格中的单元格总数是 total} = \textit{rows} \times \textit{cols。每个单元格对应一个编号，第 i 行第 j 列的单元格编号是 i \times \textit{cols} + j，其中 0 \le i < \textit{rows，0 \le j < \textit{cols。

首先遍历网格，得到猫和老鼠初始时所在的单元格以及食物所在的单元格，然后计算获胜方。

求解简化问题

这道题规定了移动次数上限为 1000，如果在 1000 次移动之内老鼠不能获胜，则猫获胜。可以首先考虑一个简化问题，在没有移动次数上限的情况下计算获胜方。该简化问题可以使用拓扑排序得到结果。

游戏中的状态由老鼠的位置、猫的位置和轮到移动的一方三个因素决定。初始时，只有边界情况的胜负结果已知，其余所有状态的结果都初始化为未知。边界情况为直接确定胜负的情况，包括三种情况：

  • 猫和老鼠在同一个单元格，无论在哪个单元格，都是猫获胜；

  • 猫和食物在同一个单元格，无论老鼠在哪个单元格，都是猫获胜；

  • 老鼠和食物在同一个单元格，只要猫和食物不在同一个单元格，无论猫在哪个单元格，都是老鼠获胜。

从边界情况出发遍历其他情况。对于当前状态，可以得到老鼠所在的单元格、猫所在的单元格和轮到移动的一方，根据当前状态可知上一轮的所有可能状态，其中上一轮的移动方和当前的移动方相反，上一轮的移动方在上一轮状态和当前状态所在的单元格相同或不同（注意可以停留在原地）。假设当前状态是老鼠所在的单元格编号是 mouse，猫所在的单元格编号是 cat，则根据当前的移动方，可以得到上一轮的所有可能状态：

  • 如果当前的移动方是老鼠，则上一轮的移动方是猫，上一轮状态中老鼠所在的单元格编号是 mouse，猫所在的单元格编号可能是 cat 或者向四个方向之一跳跃到达的单元格编号，跳跃的距离不超过 catJump 且不能跳过墙及不能跳出网格；

  • 如果当前的移动方是猫，则上一轮的移动方是老鼠，上一轮状态中猫所在的单元格编号是 cat，老鼠所在的单元格编号可能是 mouse 或者向四个方向之一跳跃到达的单元格编号，跳跃的距离不超过 mouseJump 且不能跳过墙及不能跳出网格。

对于上一轮的每一种可能的状态，如果该状态的结果已知，则不需要重复计算该状态的结果，只有对结果未知的状态，才需要计算该状态的结果。对于上一轮的移动方，只有当可以确定上一轮状态是必胜状态或者必败状态时，才更新上一轮状态的结果。

  • 如果上一轮的移动方和当前状态的获胜方相同，由于当前状态为上一轮的移动方的必胜状态，因此上一轮的移动方一定可以移动到当前状态而获胜，上一轮状态为上一轮的移动方的必胜状态。

  • 如果上一轮的移动方和当前状态的获胜方不同，则上一轮的移动方需要尝试其他可能的移动，可能有以下三种情况：

    • 如果存在一种移动可以到达上一轮的移动方的必胜状态，则上一轮状态为上一轮的移动方的必胜状态；

    • 如果所有的移动都到达上一轮的移动方的必败状态，则上一轮状态为上一轮的移动方的必败状态；

    • 如果所有的移动都不能到达上一轮的移动方的必胜状态，但是存在一种移动可以到达上一轮的移动方的未知状态，则上一轮状态为上一轮的移动方的未知状态。

其中，对于必败状态与未知状态的判断依据为上一轮的移动方可能的移动是都到达必败状态还是可以到达未知状态。为了实现必败状态与未知状态的判断，需要记录每个状态的度，初始时每个状态的度为当前玩家在当前单元格可以到达的单元格数，由于可以停留在原地，因此初始时每个状态的度为当前玩家在当前单元格可以跳跃到达的单元格数加 1。

遍历过程中，从当前状态出发遍历上一轮的所有可能状态，如果上一轮状态的结果未知且上一轮的移动方和当前状态的获胜方不同，则将上一轮状态的度减 1。如果上一轮状态的度减少到 0，则从上一轮状态出发到达的所有状态都是上一轮的移动方的必败状态，因此上一轮状态也是上一轮的移动方的必败状态。

在确定上一轮状态的结果（必胜或必败）之后，即可从上一轮状态出发，遍历其他的未知状态。当没有更多的状态可以确定胜负结果时，遍历结束，此时即可得到初始状态的结果。

求解原始问题

上述解法为简化问题的解法，没有考虑移动次数的上限。由于移动次数的限制只会影响到平局以及老鼠获胜的条件，因此只需要对平局和老鼠获胜的情况考虑移动次数。

平局对应上述解法中的未知状态，表示当猫和老鼠都按照最优策略参与游戏时，双方都无法在有限的移动次数内到达食物所在的单元格，移动次数一定会超过老鼠获胜的上限，因此未知状态对应的结果都是猫获胜。

如果在简化问题中，从初始状态开始游戏的结果是老鼠获胜，即老鼠先到达食物，则在原始问题中，需要计算从初始状态至老鼠到达食物的移动次数，只有当移动次数不超过 1000 时，老鼠才能获胜，否则猫获胜。

为了计算从初始状态至老鼠到达食物的移动次数，在拓扑排序的过程中除了记录每个状态的结果以外，还需要记录从边界情况到达每个状态的移动次数，等价于从每个状态到边界情况的移动次数。每个状态对应的移动次数计算方法如下：

  • 边界情况可以直接确定胜负，因此移动次数为 0；

  • 如果状态 s_1 和状态 s_2 相邻（即状态 s_2 是状态 s_1 的上一轮的状态之一），且状态 s_1 的结果和移动次数已知，记状态 s_1 的移动次数为 x，如果可以确定状态 s_2 的结果，则状态 s_2 的移动次数为 x + 1。

证明

对于上述解法的正确性证明，需要证明两点，一是未知状态的正确性，二是移动次数的正确性。

证明一：未知状态的正确性

遍历结束之后，如果一个状态的结果未知，则该状态满足以下两个条件：

  • 从该状态出发，任何移动都无法到达该状态的移动方的必胜状态；

  • 从该状态出发，存在一种移动可以到达未知状态。

对于结果未知的状态，如果其实际结果是该状态的移动方必胜，则一定存在一个下一轮状态，为当前状态的移动方的必胜状态，在根据下一轮状态的结果标记当前状态的结果时会将当前状态标记为当前状态的移动方的必胜状态，和结果未知矛盾。

对于结果未知的状态，如果其实际结果是该状态的移动方必败，则所有的下一轮状态都为当前状态的移动方的必败状态，在根据下一轮状态的结果标记当前状态的结果时会将当前状态标记为当前状态的移动方的必败状态，和结果未知矛盾。

因此，对于结果不是任何一方必胜的状态，实际结果一定是未知。根据游戏规则，未知状态表示在该状态下当猫和老鼠都按照最优策略参与游戏时，双方都无法在有限的移动次数内到达食物所在的单元格，移动次数一定会超过老鼠获胜的上限，因此未知状态对应的结果都是猫获胜。

证明二：移动次数的正确性

在考虑移动次数的情况下，每个玩家的最优策略应满足以下三点：

  1. 当自己可以到达必胜状态时，应将移动次数最小化；

  2. 当自己无法到达必胜状态时，如果可以避免自己到达必败状态，则应到达未知状态；

  3. 当无法避免自己到达必败状态时，应将移动次数最大化。

由于拓扑排序的实现方式是广度优先搜索，因此拓扑排序的过程中遍历状态的顺序为移动次数递增的顺序。

边界情况的移动次数为 0。从已知状态出发计算未知状态的结果和移动次数，将已知状态记为 s_1，未知状态记为 s_2，且状态 s_1 和状态 s_2 相邻（即状态 s_2 是状态 s_1 的上一轮的状态之一），记状态 s_1 的移动次数为 x，考虑以下两种情况。

  • 如果状态 s_2 的移动方和状态 s_1 的获胜方相同，则状态 s_2 的移动方会移动到状态 s_1 从而确保胜利，因此状态 s_2 的移动方必胜，移动次数为 x + 1，且该移动次数为状态 s_2 到边界情况的最少移动次数。

    假设存在另一个已知状态 s_3 的获胜方和状态 s_1 相同且状态 s_3 的移动次数小于 x，则状态 s_3 在状态 s_1 之前被遍历，在遍历到状态 s_3 时就会更新状态 s_2 的结果，和遍历到状态 s_1 时状态 s_2 的结果未知矛盾。因此状态 s_2 的最少移动次数为 x + 1。

  • 如果状态 s_2 的移动方和状态 s_1 的获胜方不同，则只有当状态 s_2 的所有相邻状态都已知是状态 s_2 的移动方的必败状态时，才能确定状态 s_2 的移动方必败。如果在遍历到状态 s_1 时可以确定状态 s_2 的结果为移动方必败，则在遍历到状态 s_1 之前，状态 s_2 的所有相邻状态都已经遍历过，即状态 s_1 是最后一个遍历到的状态 s_2 的相邻状态，因此在状态 s_2 的所有相邻状态中，状态 s_1 的移动次数最多，状态 s_2 的移动次数是 x + 1 符合必败状态下将移动次数最大化。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
MOUSE_TURN = 0
CAT_TURN = 1
UNKNOWN = 0
MOUSE_WIN = 1
CAT_WIN = 2
MAX_MOVES = 1000
DIRS = ((-1, 0), (1, 0), (0, -1), (0, 1))

class Solution:
    def canMouseWin(self, grid: List[str], catJump: int, mouseJump: int) -> bool:
        rows, cols = len(grid), len(grid[0])

        def getPos(row: int, col: int) -> int:
            return row * cols + col

        startMouse = startCat = food = 0
        for i, row in enumerate(grid):
            for j, ch in enumerate(row):
                if ch == 'M':
                    startMouse = getPos(i, j)
                elif ch == 'C':
                    startCat = getPos(i, j)
                elif ch == 'F':
                    food = getPos(i, j)

        # 计算每个状态的度
        total = rows * cols
        degrees = [[[0, 0] for _ in range(total)] for _ in range(total)]
        for mouse in range(total):
            mouseRow, mouseCol = divmod(mouse, cols)
            if grid[mouseRow][mouseCol] == '#':
                continue
            for cat in range(total):
                catRow, catCol = divmod(cat, cols)
                if grid[catRow][catCol] == '#':
                    continue
                degrees[mouse][cat][MOUSE_TURN] += 1
                degrees[mouse][cat][CAT_TURN] += 1
                for dx, dy in DIRS:
                    row, col, jump = mouseRow + dx, mouseCol + dy, 1
                    while 0 <= row < rows and 0 <= col < cols and grid[row][col] != '#' and jump <= mouseJump:
                        nextMouse = getPos(row, col)
                        nextCat = getPos(catRow, catCol)
                        degrees[nextMouse][nextCat][MOUSE_TURN] += 1
                        row += dx
                        col += dy
                        jump += 1
                    row, col, jump = catRow + dx, catCol + dy, 1
                    while 0 <= row < rows and 0 <= col < cols and grid[row][col] != '#' and jump <= catJump:
                        nextMouse = getPos(mouseRow, mouseCol)
                        nextCat = getPos(row, col)
                        degrees[nextMouse][nextCat][CAT_TURN] += 1
                        row += dx
                        col += dy
                        jump += 1

        results = [[[[0, 0], [0, 0]] for _ in range(total)] for _ in range(total)]
        q = deque()

        # 猫和老鼠在同一个单元格，猫获胜
        for pos in range(total):
            row, col = divmod(pos, cols)
            if grid[row][col] == '#':
                continue
            results[pos][pos][MOUSE_TURN][0] = CAT_WIN
            results[pos][pos][MOUSE_TURN][1] = 0
            results[pos][pos][CAT_TURN][0] = CAT_WIN
            results[pos][pos][CAT_TURN][1] = 0
            q.append((pos, pos, MOUSE_TURN))
            q.append((pos, pos, CAT_TURN))

        # 猫和食物在同一个单元格，猫获胜
        for mouse in range(total):
            mouseRow, mouseCol = divmod(mouse, cols)
            if grid[mouseRow][mouseCol] == '#' or mouse == food:
                continue
            results[mouse][food][MOUSE_TURN][0] = CAT_WIN
            results[mouse][food][MOUSE_TURN][1] = 0
            results[mouse][food][CAT_TURN][0] = CAT_WIN
            results[mouse][food][CAT_TURN][1] = 0
            q.append((mouse, food, MOUSE_TURN))
            q.append((mouse, food, CAT_TURN))

        # 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
        for cat in range(total):
            catRow, catCol = divmod(cat, cols)
            if grid[catRow][catCol] == '#' or cat == food:
                continue
            results[food][cat][MOUSE_TURN][0] = MOUSE_WIN
            results[food][cat][MOUSE_TURN][1] = 0
            results[food][cat][CAT_TURN][0] = MOUSE_WIN
            results[food][cat][CAT_TURN][1] = 0
            q.append((food, cat, MOUSE_TURN))
            q.append((food, cat, CAT_TURN))

        def getPrevStates(mouse: int, cat: int, turn: int) -> List[Tuple[int, int, int]]:
            mouseRow, mouseCol = divmod(mouse, cols)
            catRow, catCol = divmod(cat, cols)
            prevTurn = CAT_TURN if turn == MOUSE_TURN else MOUSE_TURN
            maxJump = mouseJump if prevTurn == MOUSE_TURN else catJump
            startRow = mouseRow if prevTurn == MOUSE_TURN else catRow
            startCol = mouseCol if prevTurn == MOUSE_TURN else catCol
            prevStates = [(mouse, cat, prevTurn)]
            for dx, dy in DIRS:
                i, j, jump = startRow + dx, startCol + dy, 1
                while 0 <= i < rows and 0 <= j < cols and grid[i][j] != '#' and jump <= maxJump:
                    prevMouseRow = i if prevTurn == MOUSE_TURN else mouseRow
                    prevMouseCol = j if prevTurn == MOUSE_TURN else mouseCol
                    prevCatRow = catRow if prevTurn == MOUSE_TURN else i
                    prevCatCol = catCol if prevTurn == MOUSE_TURN else j
                    prevMouse = getPos(prevMouseRow, prevMouseCol)
                    prevCat = getPos(prevCatRow, prevCatCol)
                    prevStates.append((prevMouse, prevCat, prevTurn))
                    i += dx
                    j += dy
                    jump += 1
            return prevStates

        # 拓扑排序
        while q:
            mouse, cat, turn = q.popleft()
            result = results[mouse][cat][turn][0]
            moves = results[mouse][cat][turn][1]
            for prevMouse, prevCat, prevTurn in getPrevStates(mouse, cat, turn):
                if results[prevMouse][prevCat][prevTurn][0] == UNKNOWN:
                    if result == MOUSE_WIN and prevTurn == MOUSE_TURN or result == CAT_WIN and prevTurn == CAT_TURN:
                        results[prevMouse][prevCat][prevTurn][0] = result
                        results[prevMouse][prevCat][prevTurn][1] = moves + 1
                        q.append((prevMouse, prevCat, prevTurn))
                    else:
                        degrees[prevMouse][prevCat][prevTurn] -= 1
                        if degrees[prevMouse][prevCat][prevTurn] == 0:
                            loseResult = CAT_WIN if prevTurn == MOUSE_TURN else MOUSE_WIN
                            results[prevMouse][prevCat][prevTurn][0] = loseResult
                            results[prevMouse][prevCat][prevTurn][1] = moves + 1
                            q.append((prevMouse, prevCat, prevTurn))
        return results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN and results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
class Solution {
    static final int MOUSE_TURN = 0, CAT_TURN = 1;
    static final int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
    static final int MAX_MOVES = 1000;
    int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
    int rows, cols;
    String[] grid;
    int catJump, mouseJump;
    int food;
    int[][][] degrees;
    int[][][][] results;

    public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
        this.rows = grid.length;
        this.cols = grid[0].length();
        this.grid = grid;
        this.catJump = catJump;
        this.mouseJump = mouseJump;
        int startMouse = -1, startCat = -1;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                char c = grid[i].charAt(j);
                if (c == 'M') {
                    startMouse = getPos(i, j);
                } else if (c == 'C') {
                    startCat = getPos(i, j);
                } else if (c == 'F') {
                    food = getPos(i, j);
                }
            }
        }
        int total = rows * cols;
        degrees = new int[total][total][2];
        results = new int[total][total][2][2];
        Queue<int[]> queue = new ArrayDeque<int[]>();
        // 计算每个状态的度
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow].charAt(mouseCol) == '#') {
                continue;
            }
            for (int cat = 0; cat < total; cat++) {
                int catRow = cat / cols, catCol = cat % cols;
                if (grid[catRow].charAt(catCol) == '#') {
                    continue;
                }
                degrees[mouse][cat][MOUSE_TURN]++;
                degrees[mouse][cat][CAT_TURN]++;
                for (int[] dir : dirs) {
                    for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row].charAt(col) != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
                        degrees[nextMouse][nextCat][MOUSE_TURN]++;
                    }
                    for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row].charAt(col) != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
                        degrees[nextMouse][nextCat][CAT_TURN]++;
                    }
                }
            }
        }
        // 猫和老鼠在同一个单元格，猫获胜
        for (int pos = 0; pos < total; pos++) {
            int row = pos / cols, col = pos % cols;
            if (grid[row].charAt(col) == '#') {
                continue;
            }
            results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
            results[pos][pos][MOUSE_TURN][1] = 0;
            results[pos][pos][CAT_TURN][0] = CAT_WIN;
            results[pos][pos][CAT_TURN][1] = 0;
            queue.offer(new int[]{pos, pos, MOUSE_TURN});
            queue.offer(new int[]{pos, pos, CAT_TURN});
        }
        // 猫和食物在同一个单元格，猫获胜
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow].charAt(mouseCol) == '#' || mouse == food) {
                continue;
            }
            results[mouse][food][MOUSE_TURN][0] = CAT_WIN;
            results[mouse][food][MOUSE_TURN][1] = 0;
            results[mouse][food][CAT_TURN][0] = CAT_WIN;
            results[mouse][food][CAT_TURN][1] = 0;
            queue.offer(new int[]{mouse, food, MOUSE_TURN});
            queue.offer(new int[]{mouse, food, CAT_TURN});
        }
        // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
        for (int cat = 0; cat < total; cat++) {
            int catRow = cat / cols, catCol = cat % cols;
            if (grid[catRow].charAt(catCol) == '#' || cat == food) {
                continue;
            }
            results[food][cat][MOUSE_TURN][0] = MOUSE_WIN;
            results[food][cat][MOUSE_TURN][1] = 0;
            results[food][cat][CAT_TURN][0] = MOUSE_WIN;
            results[food][cat][CAT_TURN][1] = 0;
            queue.offer(new int[]{food, cat, MOUSE_TURN});
            queue.offer(new int[]{food, cat, CAT_TURN});
        }
        // 拓扑排序
        while (!queue.isEmpty()) {
            int[] state = queue.poll();
            int mouse = state[0], cat = state[1], turn = state[2];
            int result = results[mouse][cat][turn][0];
            int moves = results[mouse][cat][turn][1];
            List<int[]> prevStates = getPrevStates(mouse, cat, turn);
            for (int[] prevState : prevStates) {
                int prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
                if (results[prevMouse][prevCat][prevTurn][0] == UNKNOWN) {
                    boolean canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                    if (canWin) {
                        results[prevMouse][prevCat][prevTurn][0] = result;
                        results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                        queue.offer(new int[]{prevMouse, prevCat, prevTurn});
                    } else {
                        degrees[prevMouse][prevCat][prevTurn]--;
                        if (degrees[prevMouse][prevCat][prevTurn] == 0) {
                            int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                            results[prevMouse][prevCat][prevTurn][0] = loseResult;
                            results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                            queue.offer(new int[]{prevMouse, prevCat, prevTurn});
                        }
                    }
                }
            }
        }
        return results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN && results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
    }

    public List<int[]> getPrevStates(int mouse, int cat, int turn) {
        List<int[]> prevStates = new ArrayList<int[]>();
        int mouseRow = mouse / cols, mouseCol = mouse % cols;
        int catRow = cat / cols, catCol = cat % cols;
        int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        int maxJump = prevTurn == MOUSE_TURN ? mouseJump : catJump;
        int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
        int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
        prevStates.add(new int[]{mouse, cat, prevTurn});
        for (int[] dir : dirs) {
            for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i].charAt(j) != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
                int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
                int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
                int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
                int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
                int prevMouse = getPos(prevMouseRow, prevMouseCol);
                int prevCat = getPos(prevCatRow, prevCatCol);
                prevStates.add(new int[]{prevMouse, prevCat, prevTurn});
            }
        }
        return prevStates;
    }

    public int getPos(int row, int col) {
        return row * cols + col;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
public class Solution {
    const int MOUSE_TURN = 0, CAT_TURN = 1;
    const int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
    const int MAX_MOVES = 1000;
    int[][] dirs = {new int[]{-1, 0}, new int[]{1, 0}, new int[]{0, -1}, new int[]{0, 1} };
    int rows, cols;
    string[] grid;
    int catJump, mouseJump;
    int food;
    int[,,] degrees;
    int[,,,] results;

    public bool CanMouseWin(string[] grid, int catJump, int mouseJump) {
        this.rows = grid.Length;
        this.cols = grid[0].Length;
        this.grid = grid;
        this.catJump = catJump;
        this.mouseJump = mouseJump;
        int startMouse = -1, startCat = -1;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                char c = grid[i][j];
                if (c == 'M') {
                    startMouse = GetPos(i, j);
                } else if (c == 'C') {
                    startCat = GetPos(i, j);
                } else if (c == 'F') {
                    food = GetPos(i, j);
                }
            }
        }
        int total = rows * cols;
        degrees = new int[total, total, 2];
        results = new int[total, total, 2, 2];
        Queue<Tuple<int, int, int>> queue = new Queue<Tuple<int, int, int>>();
        // 计算每个状态的度
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow][mouseCol] == '#') {
                continue;
            }
            for (int cat = 0; cat < total; cat++) {
                int catRow = cat / cols, catCol = cat % cols;
                if (grid[catRow][catCol] == '#') {
                    continue;
                }
                degrees[mouse, cat, MOUSE_TURN]++;
                degrees[mouse, cat, CAT_TURN]++;
                foreach (int[] dir in dirs) {
                    for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = GetPos(row, col), nextCat = GetPos(catRow, catCol);
                        degrees[nextMouse, nextCat, MOUSE_TURN]++;
                    }
                    for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = GetPos(mouseRow, mouseCol), nextCat = GetPos(row, col);
                        degrees[nextMouse, nextCat, CAT_TURN]++;
                    }
                }
            }
        }
        // 猫和老鼠在同一个单元格，猫获胜
        for (int pos = 0; pos < total; pos++) {
            int row = pos / cols, col = pos % cols;
            if (grid[row][col] == '#') {
                continue;
            }
            results[pos, pos, MOUSE_TURN, 0] = CAT_WIN;
            results[pos, pos, MOUSE_TURN, 1] = 0;
            results[pos, pos, CAT_TURN, 0] = CAT_WIN;
            results[pos, pos, CAT_TURN, 1] = 0;
            queue.Enqueue(new Tuple<int, int, int>(pos, pos, MOUSE_TURN));
            queue.Enqueue(new Tuple<int, int, int>(pos, pos, CAT_TURN));
        }
        // 猫和食物在同一个单元格，猫获胜
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow][mouseCol] == '#' || mouse == food) {
                continue;
            }
            results[mouse, food, MOUSE_TURN, 0] = CAT_WIN;
            results[mouse, food, MOUSE_TURN, 1] = 0;
            results[mouse, food, CAT_TURN, 0] = CAT_WIN;
            results[mouse, food, CAT_TURN, 1] = 0;
            queue.Enqueue(new Tuple<int, int, int>(mouse, food, MOUSE_TURN));
            queue.Enqueue(new Tuple<int, int, int>(mouse, food, CAT_TURN));
        }
        // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
        for (int cat = 0; cat < total; cat++) {
            int catRow = cat / cols, catCol = cat % cols;
            if (grid[catRow][catCol] == '#' || cat == food) {
                continue;
            }
            results[food, cat, MOUSE_TURN, 0] = MOUSE_WIN;
            results[food, cat, MOUSE_TURN, 1] = 0;
            results[food, cat, CAT_TURN, 0] = MOUSE_WIN;
            results[food, cat, CAT_TURN, 1] = 0;
            queue.Enqueue(new Tuple<int, int, int>(food, cat, MOUSE_TURN));
            queue.Enqueue(new Tuple<int, int, int>(food, cat, CAT_TURN));
        }
        // 拓扑排序
        while (queue.Count > 0) {
            Tuple<int, int, int> state = queue.Dequeue();
            int mouse = state.Item1, cat = state.Item2, turn = state.Item3;
            int result = results[mouse, cat, turn, 0];
            int moves = results[mouse, cat, turn, 1];
            IList<Tuple<int, int, int>> prevStates = GetPrevStates(mouse, cat, turn);
            foreach (Tuple<int, int, int> prevState in prevStates) {
                int prevMouse = prevState.Item1, prevCat = prevState.Item2, prevTurn = prevState.Item3;
                if (results[prevMouse, prevCat, prevTurn, 0] == UNKNOWN) {
                    bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                    if (canWin) {
                        results[prevMouse, prevCat, prevTurn, 0] = result;
                        results[prevMouse, prevCat, prevTurn, 1] = moves + 1;
                        queue.Enqueue(new Tuple<int, int, int>(prevMouse, prevCat, prevTurn));
                    } else {
                        degrees[prevMouse, prevCat, prevTurn]--;
                        if (degrees[prevMouse, prevCat, prevTurn] == 0) {
                            int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                            results[prevMouse, prevCat, prevTurn, 0] = loseResult;
                            results[prevMouse, prevCat, prevTurn, 1] = moves + 1;
                            queue.Enqueue(new Tuple<int, int, int>(prevMouse, prevCat, prevTurn));
                        }
                    }
                }
            }
        }
        return results[startMouse, startCat, MOUSE_TURN, 0] == MOUSE_WIN && results[startMouse, startCat, MOUSE_TURN, 1] <= MAX_MOVES;
    }

    public IList<Tuple<int, int, int>> GetPrevStates(int mouse, int cat, int turn) {
        IList<Tuple<int, int, int>> prevStates = new List<Tuple<int, int, int>>();
        int mouseRow = mouse / cols, mouseCol = mouse % cols;
        int catRow = cat / cols, catCol = cat % cols;
        int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        int maxJump = prevTurn == MOUSE_TURN ? mouseJump : catJump;
        int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
        int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
        prevStates.Add(new Tuple<int, int, int>(mouse, cat, prevTurn));
        foreach (int[] dir in dirs) {
            for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i][j] != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
                int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
                int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
                int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
                int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
                int prevMouse = GetPos(prevMouseRow, prevMouseCol);
                int prevCat = GetPos(prevCatRow, prevCatCol);
                prevStates.Add(new Tuple<int, int, int>(prevMouse, prevCat, prevTurn));
            }
        }
        return prevStates;
    }

    public int GetPos(int row, int col) {
        return row * cols + col;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
static const int MOUSE_TURN = 0, CAT_TURN = 1;
static const int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
static const int MAX_MOVES = 1000;

class Solution {
public: 
    vector<vector<int>> dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
    int rows, cols;
    vector<string> grid;
    int catJump, mouseJump;
    int food;
    int degrees[64][64][2];
    int results[64][64][2][2];

    bool canMouseWin(vector<string> grid, int catJump, int mouseJump) {
        this->rows = grid.size();
        this->cols = grid[0].size();
        this->grid = grid;
        this->catJump = catJump;
        this->mouseJump = mouseJump;
        int startMouse = -1, startCat = -1;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                char c = grid[i][j];
                if (c == 'M') {
                    startMouse = getPos(i, j);
                } else if (c == 'C') {
                    startCat = getPos(i, j);
                } else if (c == 'F') {
                    food = getPos(i, j);
                }
            }
        }
        int total = rows * cols;
        memset(degrees, 0, sizeof(degrees));
        memset(results, 0, sizeof(results));
        queue<tuple<int, int, int>> qu;
        // 计算每个状态的度
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow][mouseCol] == '#') {
                continue;
            }
            for (int cat = 0; cat < total; cat++) {
                int catRow = cat / cols, catCol = cat % cols;
                if (grid[catRow][catCol] == '#') {
                    continue;
                }
                degrees[mouse][cat][MOUSE_TURN]++;
                degrees[mouse][cat][CAT_TURN]++;
                for (auto & dir : dirs) {
                    for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
                        degrees[nextMouse][nextCat][MOUSE_TURN]++;
                    }
                    for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
                        int nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
                        degrees[nextMouse][nextCat][CAT_TURN]++;
                    }
                }
            }
        }
        // 猫和老鼠在同一个单元格，猫获胜
        for (int pos = 0; pos < total; pos++) {
            int row = pos / cols, col = pos % cols;
            if (grid[row][col] == '#') {
                continue;
            }
            results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
            results[pos][pos][MOUSE_TURN][1] = 0;
            results[pos][pos][CAT_TURN][0] = CAT_WIN;
            results[pos][pos][CAT_TURN][1] = 0;
            qu.emplace(pos, pos, MOUSE_TURN);
            qu.emplace(pos, pos, CAT_TURN);
        }
        // 猫和食物在同一个单元格，猫获胜
        for (int mouse = 0; mouse < total; mouse++) {
            int mouseRow = mouse / cols, mouseCol = mouse % cols;
            if (grid[mouseRow][mouseCol] == '#' || mouse == food) {
                continue;
            }
            results[mouse][food][MOUSE_TURN][0] = CAT_WIN;
            results[mouse][food][MOUSE_TURN][1] = 0;
            results[mouse][food][CAT_TURN][0] = CAT_WIN;
            results[mouse][food][CAT_TURN][1] = 0;
            qu.emplace(mouse, food, MOUSE_TURN);
            qu.emplace(mouse, food, CAT_TURN);
        }
        // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
        for (int cat = 0; cat < total; cat++) {
            int catRow = cat / cols, catCol = cat % cols;
            if (grid[catRow][catCol] == '#' || cat == food) {
                continue;
            }
            results[food][cat][MOUSE_TURN][0] = MOUSE_WIN;
            results[food][cat][MOUSE_TURN][1] = 0;
            results[food][cat][CAT_TURN][0] = MOUSE_WIN;
            results[food][cat][CAT_TURN][1] = 0;
            qu.emplace(food, cat, MOUSE_TURN);
            qu.emplace(food, cat, CAT_TURN);
        }
        // 拓扑排序
        while (!qu.empty()) {
            auto [mouse, cat, turn] = qu.front();
            qu.pop();
            int result = results[mouse][cat][turn][0];
            int moves = results[mouse][cat][turn][1];
            vector<tuple<int, int, int>> prevStates = getPrevStates(mouse, cat, turn);
            for (auto [prevMouse, prevCat, prevTurn] : prevStates) {
                if (results[prevMouse][prevCat][prevTurn][0] == UNKNOWN) {
                    bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                    if (canWin) {
                        results[prevMouse][prevCat][prevTurn][0] = result;
                        results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                        qu.emplace(prevMouse, prevCat, prevTurn);
                    } else {
                        degrees[prevMouse][prevCat][prevTurn]--;
                        if (degrees[prevMouse][prevCat][prevTurn] == 0) {
                            int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                            results[prevMouse][prevCat][prevTurn][0] = loseResult;
                            results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                            qu.emplace(prevMouse, prevCat, prevTurn);
                        }
                    }
                }
            }
        }
        return results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN && results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
    }
    
    vector<tuple<int, int, int>> getPrevStates(int mouse, int cat, int turn) {
        vector<tuple<int, int, int>> prevStates;
        int mouseRow = mouse / cols, mouseCol = mouse % cols;
        int catRow = cat / cols, catCol = cat % cols;
        int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        int maxJump = prevTurn == MOUSE_TURN ? mouseJump : catJump;
        int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
        int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
        prevStates.emplace_back(mouse, cat, prevTurn);
        for (auto & dir : dirs) {
            for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i][j] != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
                int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
                int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
                int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
                int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
                int prevMouse = getPos(prevMouseRow, prevMouseCol);
                int prevCat = getPos(prevCatRow, prevCatCol);
                prevStates.emplace_back(prevMouse, prevCat, prevTurn);
            }
        }
        return prevStates;
    }

    int getPos(int row, int col) {
        return row * cols + col;
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
static const int MOUSE_TURN = 0, CAT_TURN = 1;
static const int UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
static const int MAX_MOVES = 1000;

#define MAX_QUEUE_SIZE 10000

int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
int g_rows, g_cols;
char **g_grid;
int g_catJump, g_mouseJump;
int g_food;
int g_degrees[64][64][2];
int g_results[64][64][2][2];

int getPos(int row, int col) {
    return row * g_cols + col;
}

typedef struct State {
    int mouse;
    int cat;
    int turn;
} State;

typedef struct Node {
    State currState;
    struct Node * next;
} Node;

Node * getPrevStates(int mouse, int cat, int turn) {
    Node * prevStates = NULL;
    Node * tail = NULL;
    int mouseRow = mouse / g_cols, mouseCol = mouse % g_cols;
    int catRow = cat / g_cols, catCol = cat % g_cols;
    int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
    int maxJump = prevTurn == MOUSE_TURN ? g_mouseJump : g_catJump;
    int startRow = prevTurn == MOUSE_TURN ? mouseRow : catRow;
    int startCol = prevTurn == MOUSE_TURN ? mouseCol : catCol;
    prevStates = (Node *)malloc(sizeof(Node));
    tail = prevStates;
    tail->currState.mouse = mouse;
    tail->currState.cat = cat;
    tail->currState.turn = prevTurn;
    tail->next = NULL;
    for (int k = 0; k < 4; k++) {
        int *dir = dirs[k];
        for (int i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < g_rows && j >= 0 && j < g_cols && g_grid[i][j] != '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
            int prevMouseRow = prevTurn == MOUSE_TURN ? i : mouseRow;
            int prevMouseCol = prevTurn == MOUSE_TURN ? j : mouseCol;
            int prevCatRow = prevTurn == MOUSE_TURN ? catRow : i;
            int prevCatCol = prevTurn == MOUSE_TURN ? catCol : j;
            int prevMouse = getPos(prevMouseRow, prevMouseCol);
            int prevCat = getPos(prevCatRow, prevCatCol);
            tail->next = (Node *)malloc(sizeof(Node));
            tail = tail->next;
            tail->currState.mouse = prevMouse;
            tail->currState.cat = prevCat;
            tail->currState.turn = prevTurn;
            tail->next = NULL;
        }
    }
    return prevStates;
}

bool canMouseWin(char ** grid, int gridSize, int catJump, int mouseJump){
    g_rows = gridSize;
    g_cols = strlen(grid[0]);
    g_grid = grid;
    g_catJump = catJump;
    g_mouseJump = mouseJump;
    int startMouse = -1, startCat = -1;
    for (int i = 0; i < g_rows; i++) {
        for (int j = 0; j < g_cols; j++) {
            char c = grid[i][j];
            if (c == 'M') {
                startMouse = getPos(i, j);
            } else if (c == 'C') {
                startCat = getPos(i, j);
            } else if (c == 'F') {
                g_food = getPos(i, j);
            }
        }
    }
    int total = g_rows * g_cols;
    memset(g_degrees, 0, sizeof(g_degrees));
    memset(g_results, 0, sizeof(g_results));
    State * queue = (State *)malloc(sizeof(State) * MAX_QUEUE_SIZE);
    int head = 0, tail = 0;
    // 计算每个状态的度
    for (int mouse = 0; mouse < total; mouse++) {
        int mouseRow = mouse / g_cols, mouseCol = mouse % g_cols;
        if (grid[mouseRow][mouseCol] == '#') {
            continue;
        }
        for (int cat = 0; cat < total; cat++) {
            int catRow = cat / g_cols, catCol = cat % g_cols;
            if (grid[catRow][catCol] == '#') {
                continue;
            }
            g_degrees[mouse][cat][MOUSE_TURN]++;
            g_degrees[mouse][cat][CAT_TURN]++;
            for (int i = 0; i < 4; i++) {
                int * dir = dirs[i];
                for (int row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < g_rows && col >= 0 && col < g_cols && grid[row][col] != '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
                    int nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
                    g_degrees[nextMouse][nextCat][MOUSE_TURN]++;
                }
                for (int row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < g_rows && col >= 0 && col < g_cols && grid[row][col] != '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
                    int nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
                    g_degrees[nextMouse][nextCat][CAT_TURN]++;
                }
            }
        }
    }
    // 猫和老鼠在同一个单元格，猫获胜
    for (int pos = 0; pos < total; pos++) {
        int row = pos / g_cols, col = pos % g_cols;
        if (grid[row][col] == '#') {
            continue;
        }
        g_results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
        g_results[pos][pos][MOUSE_TURN][1] = 0;
        g_results[pos][pos][CAT_TURN][0] = CAT_WIN;
        g_results[pos][pos][CAT_TURN][1] = 0;
        queue[tail].mouse = pos;
        queue[tail].cat = pos;
        queue[tail].turn = MOUSE_TURN;
        tail++;
        queue[tail].mouse = pos;
        queue[tail].cat = pos;
        queue[tail].turn = CAT_TURN;
        tail++;
    }
    // 猫和食物在同一个单元格，猫获胜
    for (int mouse = 0; mouse < total; mouse++) {
        int mouseRow = mouse / g_cols, mouseCol = mouse % g_cols;
        if (grid[mouseRow][mouseCol] == '#' || mouse == g_food) {
            continue;
        }
        g_results[mouse][g_food][MOUSE_TURN][0] = CAT_WIN;
        g_results[mouse][g_food][MOUSE_TURN][1] = 0;
        g_results[mouse][g_food][CAT_TURN][0] = CAT_WIN;
        g_results[mouse][g_food][CAT_TURN][1] = 0;
        queue[tail].mouse = mouse;
        queue[tail].cat = g_food;
        queue[tail].turn = MOUSE_TURN;
        tail++;
        queue[tail].mouse = mouse;
        queue[tail].cat = g_food;
        queue[tail].turn = CAT_TURN;
        tail++;
    }
    // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
    for (int cat = 0; cat < total; cat++) {
        int catRow = cat / g_cols, catCol = cat % g_cols;
        if (grid[catRow][catCol] == '#' || cat == g_food) {
            continue;
        }
        g_results[g_food][cat][MOUSE_TURN][0] = MOUSE_WIN;
        g_results[g_food][cat][MOUSE_TURN][1] = 0;
        g_results[g_food][cat][CAT_TURN][0] = MOUSE_WIN;
        g_results[g_food][cat][CAT_TURN][1] = 0;
        queue[tail].mouse = g_food;
        queue[tail].cat = cat;
        queue[tail].turn = MOUSE_TURN;
        tail++;
        queue[tail].mouse = g_food;
        queue[tail].cat = cat;
        queue[tail].turn = CAT_TURN;
        tail++;
    }
    // 拓扑排序
    while (head != tail) {
        int mouse = queue[head].mouse;
        int cat = queue[head].cat;
        int turn = queue[head].turn;
        head++;
        int result = g_results[mouse][cat][turn][0];
        int moves = g_results[mouse][cat][turn][1];
        Node * prevStates = getPrevStates(mouse, cat, turn);
        for (Node * curr = prevStates; curr; curr = curr->next) {
            int prevMouse = curr->currState.mouse;
            int prevCat = curr->currState.cat;
            int prevTurn = curr->currState.turn;
            if (g_results[prevMouse][prevCat][prevTurn][0] == UNKNOWN) {
                bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                if (canWin) {
                    g_results[prevMouse][prevCat][prevTurn][0] = result;
                    g_results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                    queue[tail].mouse = prevMouse;
                    queue[tail].cat = prevCat;
                    queue[tail].turn = prevTurn;
                    tail++;
                } else {
                    g_degrees[prevMouse][prevCat][prevTurn]--;
                    if (g_degrees[prevMouse][prevCat][prevTurn] == 0) {
                        int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                        g_results[prevMouse][prevCat][prevTurn][0] = loseResult;
                        g_results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                        queue[tail].mouse = prevMouse;
                        queue[tail].cat = prevCat;
                        queue[tail].turn = prevTurn;
                        tail++;
                    }
                }
            }
        }
    }
    free(queue);
    return g_results[startMouse][startCat][MOUSE_TURN][0] == MOUSE_WIN && g_results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
const MOUSE_TURN = 0, CAT_TURN = 1;
const UNKNOWN = 0, MOUSE_WIN = 1, CAT_WIN = 2;
const MAX_MOVES = 1000;
const dirs = [[-1, 0], [1, 0], [0, -1], [0, 1]];
var canMouseWin = function(grid, catJump, mouseJump) {
    this.rows = grid.length;
    this.cols = grid[0].length;
    let startMouse = -1, startCat = -1;

    const getPos = (row, col) => {
        return row * this.cols + col;
    };

    const getPrevStates = (mouse, cat, turn) => {
        const prevStates = [];
        const mouseRow = Math.floor(mouse / this.cols), mouseCol = mouse % this.cols;
        const catRow = Math.floor(cat / this.cols), catCol = cat % this.cols;
        const prevTurn = turn === MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        const maxJump = prevTurn === MOUSE_TURN ? mouseJump : catJump;
        const startRow = prevTurn === MOUSE_TURN ? mouseRow : catRow;
        const startCol = prevTurn === MOUSE_TURN ? mouseCol : catCol;
        prevStates.push([mouse, cat, prevTurn]);
        for (const dir of dirs) {
            for (let i = startRow + dir[0], j = startCol + dir[1], jump = 1; i >= 0 && i < rows && j >= 0 && j < this.cols && grid[i].charAt(j) !== '#' && jump <= maxJump; i += dir[0], j += dir[1], jump++) {
                const prevMouseRow = prevTurn === MOUSE_TURN ? i : mouseRow;
                const prevMouseCol = prevTurn === MOUSE_TURN ? j : mouseCol;
                const prevCatRow = prevTurn === MOUSE_TURN ? catRow : i;
                const prevCatCol = prevTurn === MOUSE_TURN ? catCol : j;
                const prevMouse = getPos(prevMouseRow, prevMouseCol);
                const prevCat = getPos(prevCatRow, prevCatCol);
                prevStates.push([prevMouse, prevCat, prevTurn]);
            }
        }
        return prevStates;
    }

    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < this.cols; j++) {
            const c = grid[i][j];
            if (c === 'M') {
                startMouse = getPos(i, j);
            } else if (c === 'C') {
                startCat = getPos(i, j);
            } else if (c === 'F') {
                food = getPos(i, j);
            }
        }
    }
    const total = rows * this.cols;
    const degrees = new Array(total).fill(0).map(() => new Array(total).fill(0).map(() => new Array(2).fill(0)));
    const results = new Array(total).fill(0).map(() => new Array(total).fill(0).map(() => new Array(2).fill(0).map(() => new Array(2).fill(0))));
    const queue = [];
    // 计算每个状态的度
    for (let mouse = 0; mouse < total; mouse++) {
        let mouseRow = Math.floor(mouse / this.cols), mouseCol = mouse % this.cols;
        if (grid[mouseRow][mouseCol] === '#') {
            continue;
        }
        for (let cat = 0; cat < total; cat++) {
            let catRow = Math.floor(cat / this.cols), catCol = cat % this.cols;
            if (grid[catRow][catCol] === '#') {
                continue;
            }
            degrees[mouse][cat][MOUSE_TURN]++;
            degrees[mouse][cat][CAT_TURN]++;
            for (const dir of dirs) {
                for (let row = mouseRow + dir[0], col = mouseCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < this.cols && grid[row][col] !== '#' && jump <= mouseJump; row += dir[0], col += dir[1], jump++) {
                    const nextMouse = getPos(row, col), nextCat = getPos(catRow, catCol);
                    degrees[nextMouse][nextCat][MOUSE_TURN]++;
                }
                for (let row = catRow + dir[0], col = catCol + dir[1], jump = 1; row >= 0 && row < rows && col >= 0 && col < this.cols && grid[row][col] !== '#' && jump <= catJump; row += dir[0], col += dir[1], jump++) {
                    const nextMouse = getPos(mouseRow, mouseCol), nextCat = getPos(row, col);
                    degrees[nextMouse][nextCat][CAT_TURN]++;
                }
            }
        }
    }
    // 猫和老鼠在同一个单元格，猫获胜
    for (let pos = 0; pos < total; pos++) {
        const row = Math.floor(pos / this.cols), col = pos % this.cols;
        if (grid[row][col] === '#') {
            continue;
        }
        results[pos][pos][MOUSE_TURN][0] = CAT_WIN;
        results[pos][pos][MOUSE_TURN][1] = 0;
        results[pos][pos][CAT_TURN][0] = CAT_WIN;
        results[pos][pos][CAT_TURN][1] = 0;
        queue.push([pos, pos, MOUSE_TURN]);
        queue.push([pos, pos, CAT_TURN]);
    }
    // 猫和食物在同一个单元格，猫获胜
    for (let mouse = 0; mouse < total; mouse++) {
        const mouseRow = Math.floor(mouse / this.cols), mouseCol = mouse % this.cols;
        if (grid[mouseRow][mouseCol] === '#' || mouse === food) {
            continue;
        }
        results[mouse][food][MOUSE_TURN][0] = CAT_WIN;
        results[mouse][food][MOUSE_TURN][1] = 0;
        results[mouse][food][CAT_TURN][0] = CAT_WIN;
        results[mouse][food][CAT_TURN][1] = 0;
        queue.push([mouse, food, MOUSE_TURN]);
        queue.push([mouse, food, CAT_TURN]);
    }
    // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
    for (let cat = 0; cat < total; cat++) {
        const catRow = Math.floor(cat / this.cols), catCol = cat % this.cols;
        if (grid[catRow][catCol] === '#' || cat === food) {
            continue;
        }
        results[food][cat][MOUSE_TURN][0] = MOUSE_WIN;
        results[food][cat][MOUSE_TURN][1] = 0;
        results[food][cat][CAT_TURN][0] = MOUSE_WIN;
        results[food][cat][CAT_TURN][1] = 0;
        queue.push([food, cat, MOUSE_TURN]);
        queue.push([food, cat, CAT_TURN]);
    }
    // 拓扑排序
    while (queue.length) {
        const state = queue.shift();
        const mouse = state[0], cat = state[1], turn = state[2];
        const result = results[mouse][cat][turn][0];
        const moves = results[mouse][cat][turn][1];
        const prevStates = getPrevStates(mouse, cat, turn);
        for (const prevState of prevStates) {
            const prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
            if (results[prevMouse][prevCat][prevTurn][0] === UNKNOWN) {
                const canWin = (result === MOUSE_WIN && prevTurn === MOUSE_TURN) || (result === CAT_WIN && prevTurn === CAT_TURN);
                if (canWin) {
                    results[prevMouse][prevCat][prevTurn][0] = result;
                    results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                    queue.push([prevMouse, prevCat, prevTurn]);
                } else {
                    degrees[prevMouse][prevCat][prevTurn]--;
                    if (degrees[prevMouse][prevCat][prevTurn] === 0) {
                        const loseResult = prevTurn === MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                        results[prevMouse][prevCat][prevTurn][0] = loseResult;
                        results[prevMouse][prevCat][prevTurn][1] = moves + 1;
                        queue.push([prevMouse, prevCat, prevTurn]);
                    }
                }
            }
        }
    }

    return results[startMouse][startCat][MOUSE_TURN][0] === MOUSE_WIN && results[startMouse][startCat][MOUSE_TURN][1] <= MAX_MOVES;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
const (
    MouseTurn = 0
    CatTurn   = 1
    UNKNOWN   = 0
    MouseWin  = 1
    CatWin    = 2
    MaxMoves  = 1000
)

var dirs = []struct{ x, y int }{ {-1, 0}, {1, 0}, {0, -1}, {0, 1} }

func canMouseWin(grid []string, catJump int, mouseJump int) bool {
    rows, cols := len(grid), len(grid[0])
    getPos := func(row, col int) int { return row*cols + col }
    var startMouse, startCat, food int
    for i, row := range grid {
        for j, ch := range row {
            if ch == 'M' {
                startMouse = getPos(i, j)
            } else if ch == 'C' {
                startCat = getPos(i, j)
            } else if ch == 'F' {
                food = getPos(i, j)
            }
        }
    }

    // 计算每个状态的度
    total := rows * cols
    degrees := [64][64][2]int{}
    for mouse := 0; mouse < total; mouse++ {
        mouseRow := mouse / cols
        mouseCol := mouse % cols
        if grid[mouseRow][mouseCol] == '#' {
            continue
        }
        for cat := 0; cat < total; cat++ {
            catRow := cat / cols
            catCol := cat % cols
            if grid[catRow][catCol] == '#' {
                continue
            }
            degrees[mouse][cat][MouseTurn]++
            degrees[mouse][cat][CatTurn]++
            for _, dir := range dirs {
                for row, col, jump := mouseRow+dir.x, mouseCol+dir.y, 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= mouseJump; jump++ {
                    nextMouse := getPos(row, col)
                    nextCat := getPos(catRow, catCol)
                    degrees[nextMouse][nextCat][MouseTurn]++
                    row += dir.x
                    col += dir.y
                }
                for row, col, jump := catRow+dir.x, catCol+dir.y, 1; row >= 0 && row < rows && col >= 0 && col < cols && grid[row][col] != '#' && jump <= catJump; jump++ {
                    nextMouse := getPos(mouseRow, mouseCol)
                    nextCat := getPos(row, col)
                    degrees[nextMouse][nextCat][CatTurn]++
                    row += dir.x
                    col += dir.y
                }
            }
        }
    }

    results := [64][64][2][2]int{}
    type state struct{ mouse, cat, turn int }
    q := []state{}

    // 猫和老鼠在同一个单元格，猫获胜
    for pos := 0; pos < total; pos++ {
        row := pos / cols
        col := pos % cols
        if grid[row][col] == '#' {
            continue
        }
        results[pos][pos][MouseTurn][0] = CatWin
        results[pos][pos][MouseTurn][1] = 0
        results[pos][pos][CatTurn][0] = CatWin
        results[pos][pos][CatTurn][1] = 0
        q = append(q, state{pos, pos, MouseTurn}, state{pos, pos, CatTurn})
    }

    // 猫和食物在同一个单元格，猫获胜
    for mouse := 0; mouse < total; mouse++ {
        mouseRow := mouse / cols
        mouseCol := mouse % cols
        if grid[mouseRow][mouseCol] == '#' || mouse == food {
            continue
        }
        results[mouse][food][MouseTurn][0] = CatWin
        results[mouse][food][MouseTurn][1] = 0
        results[mouse][food][CatTurn][0] = CatWin
        results[mouse][food][CatTurn][1] = 0
        q = append(q, state{mouse, food, MouseTurn}, state{mouse, food, CatTurn})
    }

    // 老鼠和食物在同一个单元格且猫和食物不在同一个单元格，老鼠获胜
    for cat := 0; cat < total; cat++ {
        catRow := cat / cols
        catCol := cat % cols
        if grid[catRow][catCol] == '#' || cat == food {
            continue
        }
        results[food][cat][MouseTurn][0] = MouseWin
        results[food][cat][MouseTurn][1] = 0
        results[food][cat][CatTurn][0] = MouseWin
        results[food][cat][CatTurn][1] = 0
        q = append(q, state{food, cat, MouseTurn}, state{food, cat, CatTurn})
    }

    getPrevStates := func(mouse, cat, turn int) []state {
        mouseRow := mouse / cols
        mouseCol := mouse % cols
        catRow := cat / cols
        catCol := cat % cols
        prevTurn := MouseTurn
        if turn == MouseTurn {
            prevTurn = CatTurn
        }
        maxJump, startRow, startCol := catJump, catRow, catCol
        if prevTurn == MouseTurn {
            maxJump, startRow, startCol = mouseJump, mouseRow, mouseCol
        }
        prevStates := []state{ {mouse, cat, prevTurn} }
        for _, dir := range dirs {
            for i, j, jump := startRow+dir.x, startCol+dir.y, 1; i >= 0 && i < rows && j >= 0 && j < cols && grid[i][j] != '#' && jump <= maxJump; jump++ {
                prevMouseRow := mouseRow
                prevMouseCol := mouseCol
                prevCatRow := i
                prevCatCol := j
                if prevTurn == MouseTurn {
                    prevMouseRow = i
                    prevMouseCol = j
                    prevCatRow = catRow
                    prevCatCol = catCol
                }
                prevMouse := getPos(prevMouseRow, prevMouseCol)
                prevCat := getPos(prevCatRow, prevCatCol)
                prevStates = append(prevStates, state{prevMouse, prevCat, prevTurn})
                i += dir.x
                j += dir.y
            }
        }
        return prevStates
    }

    // 拓扑排序
    for len(q) > 0 {
        s := q[0]
        q = q[1:]
        mouse, cat, turn := s.mouse, s.cat, s.turn
        result := results[mouse][cat][turn][0]
        moves := results[mouse][cat][turn][1]
        for _, s := range getPrevStates(mouse, cat, turn) {
            prevMouse, prevCat, prevTurn := s.mouse, s.cat, s.turn
            if results[prevMouse][prevCat][prevTurn][0] == UNKNOWN {
                canWin := result == MouseWin && prevTurn == MouseTurn || result == CatWin && prevTurn == CatTurn
                if canWin {
                    results[prevMouse][prevCat][prevTurn][0] = result
                    results[prevMouse][prevCat][prevTurn][1] = moves + 1
                    q = append(q, state{prevMouse, prevCat, prevTurn})
                } else {
                    degrees[prevMouse][prevCat][prevTurn]--
                    if degrees[prevMouse][prevCat][prevTurn] == 0 {
                        loseResult := MouseWin
                        if prevTurn == MouseTurn {
                            loseResult = CatWin
                        }
                        results[prevMouse][prevCat][prevTurn][0] = loseResult
                        results[prevMouse][prevCat][prevTurn][1] = moves + 1
                        q = append(q, state{prevMouse, prevCat, prevTurn})
                    }
                }
            }
        }
    }
    return results[startMouse][startCat][MouseTurn][0] == MouseWin && results[startMouse][startCat][MouseTurn][1] <= MaxMoves
}

复杂度分析

  • 时间复杂度：O(\textit{rows}^2 \times \textit{cols}^2 \times (\textit{rows} + \textit{cols}))，其中 rows 和 cols 分别是网格的行数和列数。状态数是 O(\textit{rows}^2 \times \textit{cols}^2)，对于每个状态需要 O(\textit{rows} + \textit{cols}) 的时间计算状态值，因此总时间复杂度是 O(\textit{rows}^2 \times \textit{cols}^2 \times (\textit{rows} + \textit{cols}))。

  • 空间复杂度：O(\textit{rows}^2 \times \textit{cols}^2)，其中 rows 和 cols 分别是网格的行数和列数。需要记录每个状态的度和结果，状态数是 O(\textit{rows}^2 \times \textit{cols}^2)。

 Comments
On this page
1728-猫和老鼠 II