1738-找出第 K 大的异或坐标值

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:32 2023-09-13 16:06:32 Updated    

给你一个二维矩阵 matrix 和一个整数 k ，矩阵大小为 m x n 由非负整数组成。

矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素
matrix[i][j]（ 下标从 0 开始计数 ）执行异或运算得到。

请你找出 matrix 的所有坐标中第 k 大的值（ k 的值从 1 开始计数）。

示例 1：

**输入：** matrix = [[5,2],[1,6]], k = 1
**输出：** 7
**解释：** 坐标 (0,1) 的值是 5 XOR 2 = 7 ，为最大的值。

示例 2：

**输入：** matrix = [[5,2],[1,6]], k = 2
**输出：** 5
**解释：** 坐标 (0,0) 的值是 5 = 5 ，为第 2 大的值。

示例 3：

**输入：** matrix = [[5,2],[1,6]], k = 3
**输出：** 4
**解释：** 坐标 (1,0) 的值是 5 XOR 1 = 4 ，为第 3 大的值。

示例 4：

**输入：** matrix = [[5,2],[1,6]], k = 4
**输出：** 0
**解释：** 坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ，为第 4 大的值。

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 1000
  • 0 <= matrix[i][j] <= 106
  • 1 <= k <= m * n

前言

思路与算法

我们用 \oplus 表示按位异或运算。

由于「按位异或运算」与「加法运算」有着十分相似的性质，它们都满足交换律：

a \oplus b = b \oplus a

以及结合律：

(a \oplus b) \oplus c = a \oplus (b \oplus c)

因此我们可以使用「前缀和」这一技巧对按位异或运算的结果进行维护。由于本题中给定的矩阵 matrix 是二维的，因此我们需要使用二维前缀和。

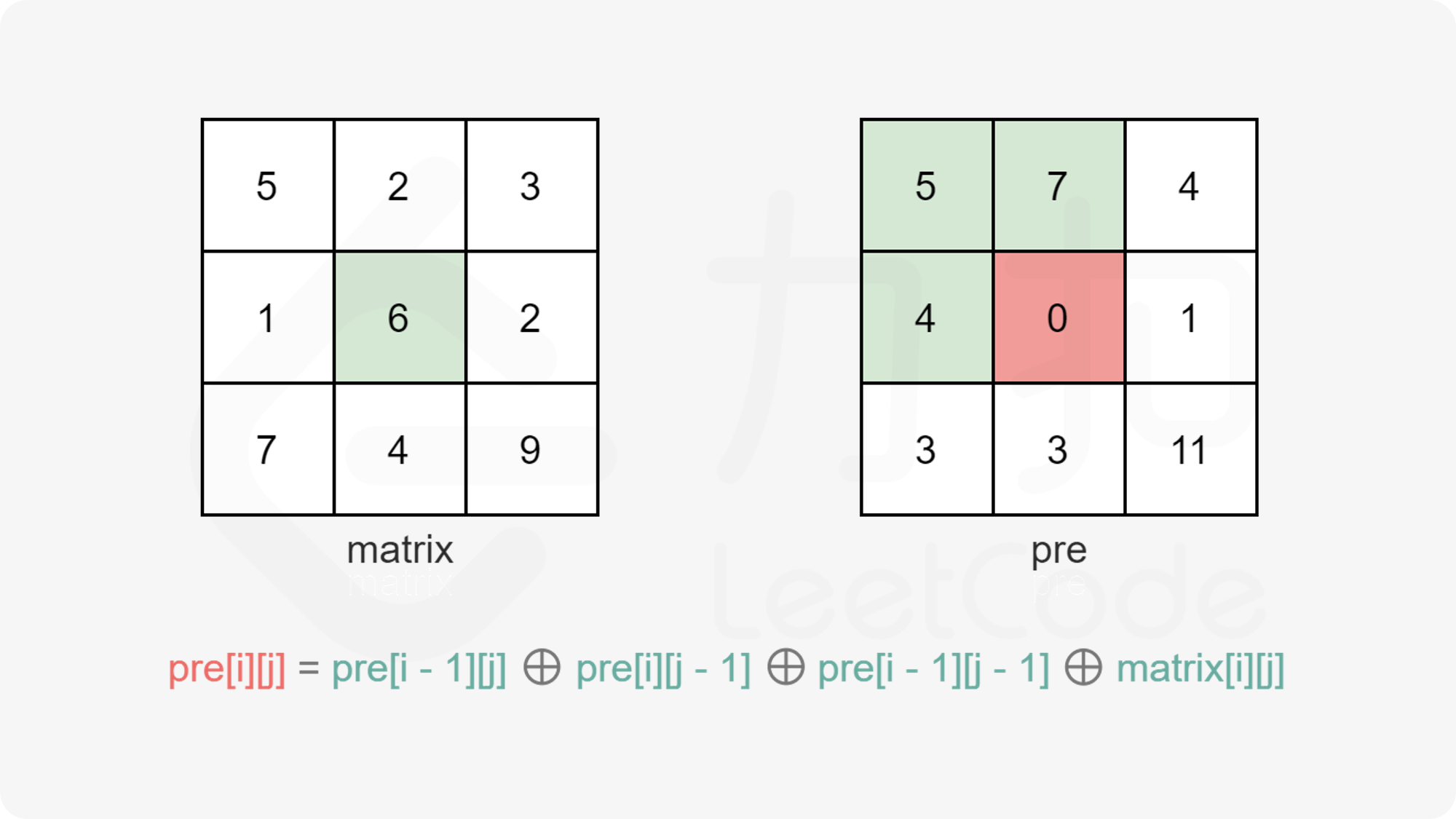
设二维前缀和 pre}(i, j) 表示矩阵 matrix 中所有满足 0 \leq x < i 且 0 \leq y < j 的元素执行按位异或运算的结果。与一维前缀和类似，要想快速得到 pre}(i, j)，我们需要已经知道 pre}(i-1, j)，pre}(i, j-1) 以及 pre}(i-1,j-1) 的结果，即：

\textit{pre}(i, j) = \textit{pre}(i-1, j) \oplus \textit{pre}(i, j-1) \oplus \textit{pre}(i-1, j-1) \oplus \textit{matrix}(i, j)

下图给出了该二维前缀和递推式的可视化展示。

fig1

当我们将 pre}(i-1, j) 和 pre}(i, j-1) 进行按位异或运算后，由于对一个数 x 异或两次 y，结果仍然为 x 本身，即：

x \oplus y \oplus y = x

因此 pre}(i-1, j-1) 对应区域的按位异或结果被抵消，我们需要将其补上，并对位置 (i, j) 的元素进行按位异或运算，这样就得到了 pre}(i, j)。

在得到了所有的二维前缀和之后，我们只需要找出其中第 k 大的元素即为答案。这一步我们可以直接将 mn 个二维前缀和进行排序后返第 k 大的元素，也可以参考「215. 数组中的第 K 个最大元素的官方题解 」中时间复杂度更低的做法。

下面的方法一给出的是基于排序的解法，方法二给出的是基于快速排序思路的、时间复杂度更低的快速选择算法的解法。

细节

在二维前缀和的计算过程中，如果我们正在计算首行或者首列，即 i=0 或 j=0，此时例如 pre}(i-1,j-1) 是一个超出下标范围的结果。因此我们可以使用一个 (m+1) \times (n+1) 的二维矩阵，将首行和首列空出来赋予默认值 0，并使用接下来的 m 行和 n 列存储二维前缀和，这样就不必进行下标范围的判断了。

方法一：二维前缀和 + 排序

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> pre(m + 1, vector<int>(n + 1));
        vector<int> results;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                results.push_back(pre[i][j]);
            }
        }

        sort(results.begin(), results.end(), greater<int>());
        return results[k - 1];
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int kthLargestValue(int[][] matrix, int k) {
        int m = matrix.length, n = matrix[0].length;
        int[][] pre = new int[m + 1][n + 1];
        List<Integer> results = new ArrayList<Integer>();
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                results.add(pre[i][j]);
            }
        }

        Collections.sort(results, new Comparator<Integer>() {
            public int compare(Integer num1, Integer num2) {
                return num2 - num1;
            }
        });
        return results.get(k - 1);
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public int KthLargestValue(int[][] matrix, int k) {
        int m = matrix.Length, n = matrix[0].Length;
        int[,] pre = new int[m + 1, n + 1];
        List<int> results = new List<int>();
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i, j] = pre[i - 1, j] ^ pre[i, j - 1] ^ pre[i - 1, j - 1] ^ matrix[i - 1][j - 1];
                results.Add(pre[i, j]);
            }
        }

        results.Sort(
            delegate(int num1, int num2) {
                return num2 - num1;
            }
        );
        return results[k - 1];
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
        m, n = len(matrix), len(matrix[0])
        pre = [[0] * (n + 1) for _ in range(m + 1)]
        results = list()
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1]
                results.append(pre[i][j])

        results.sort(reverse=True)
        return results[k - 1]
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func kthLargestValue(matrix [][]int, k int) int {
    m, n := len(matrix), len(matrix[0])
    results := make([]int, 0, m*n)
    pre := make([][]int, m+1)
    pre[0] = make([]int, n+1)
    for i, row := range matrix {
        pre[i+1] = make([]int, n+1)
        for j, val := range row {
            pre[i+1][j+1] = pre[i+1][j] ^ pre[i][j+1] ^ pre[i][j] ^ val
            results = append(results, pre[i+1][j+1])
        }
    }
    sort.Sort(sort.Reverse(sort.IntSlice(results)))
    return results[k-1]
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int cmp(int* a, int* b) {
    return *b - *a;
}

int kthLargestValue(int** matrix, int matrixSize, int* matrixColSize, int k) {
    int m = matrixSize, n = matrixColSize[0];
    int pre[m + 1][n + 1];
    memset(pre, 0, sizeof(pre));
    int results[m * n], resultsSize = 0;
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
            results[resultsSize++] = pre[i][j];
        }
    }

    qsort(results, resultsSize, sizeof(int), cmp);
    return results[k - 1];
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
var kthLargestValue = function(matrix, k) {
    const m = matrix.length, n = matrix[0].length;
    const pre = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    const results = [];
    for (let i = 1; i < m + 1; i++) {
        for (let j = 1; j < n + 1; j++) {
            pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
            results.push(pre[i][j]);
        }
    }
    results.sort((a, b) => b - a);
    return results[k - 1];
}

复杂度分析

  • 时间复杂度：O(mn \log (mn))。计算二维前缀和的时间复杂度为 O(mn)，排序的时间复杂度为 O(mn \log (mn))，因此总时间复杂度为 O(mn \log (mn))。

  • 空间复杂度：O(mn)，即为存储二维前缀和需要的空间。

方法二：二维前缀和 + 快速选择算法

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> pre(m + 1, vector<int>(n + 1));
        vector<int> results;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                results.push_back(pre[i][j]);
            }
        }

        nth_element(results.begin(), results.begin() + k - 1, results.end(), greater<int>());
        return results[k - 1];
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int kthLargestValue(int[][] matrix, int k) {
        int m = matrix.length, n = matrix[0].length;
        int[][] pre = new int[m + 1][n + 1];
        List<Integer> results = new ArrayList<Integer>();
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                results.add(pre[i][j]);
            }
        }

        nthElement(results, 0, k - 1, results.size() - 1);
        return results.get(k - 1);
    }

    public void nthElement(List<Integer> results, int left, int kth, int right) {
        if (left == right) {
            return;
        }
        int pivot = (int) (left + Math.random() * (right - left + 1));
        swap(results, pivot, right);
        // 三路划分（three-way partition）
        int sepl = left - 1, sepr = left - 1;
        for (int i = left; i <= right; i++) {
            if (results.get(i) > results.get(right)) {
                swap(results, ++sepr, i);
                swap(results, ++sepl, sepr);
            } else if (results.get(i) == results.get(right)) {
                swap(results, ++sepr, i);
            }
        }
        if (sepl < left + kth && left + kth <= sepr) {
            return;
        } else if (left + kth <= sepl) {
            nthElement(results, left, kth, sepl);
        } else {
            nthElement(results, sepr + 1, kth - (sepr - left + 1), right);
        }
    }

    public void swap(List<Integer> results, int index1, int index2) {
        int temp = results.get(index1);
        results.set(index1, results.get(index2));
        results.set(index2, temp);
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public class Solution {
    Random random = new Random();

    public int KthLargestValue(int[][] matrix, int k) {
        int m = matrix.Length, n = matrix[0].Length;
        int[,] pre = new int[m + 1, n + 1];
        List<int> results = new List<int>();
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                pre[i, j] = pre[i - 1, j] ^ pre[i, j - 1] ^ pre[i - 1, j - 1] ^ matrix[i - 1][j - 1];
                results.Add(pre[i, j]);
            }
        }

        NthElement(results, 0, k - 1, results.Count - 1);
        return results[k - 1];
    }

    public void NthElement(List<int> results, int left, int kth, int right) {
        if (left == right) {
            return;
        }
        int pivot = random.Next(left, right + 1);
        Swap(results, pivot, right);
        // 三路划分（three-way partition）
        int sepl = left - 1, sepr = left - 1;
        for (int i = left; i <= right; i++) {
            if (results[i] > results[right]) {
                Swap(results, ++sepr, i);
                Swap(results, ++sepl, sepr);
            } else if (results[i] == results[right]) {
                Swap(results, ++sepr, i);
            }
        }
        if (sepl < left + kth && left + kth <= sepr) {
            return;
        } else if (left + kth <= sepl) {
            NthElement(results, left, kth, sepl);
        } else {
            NthElement(results, sepr + 1, kth - (sepr - left + 1), right);
        }
    }

    public void Swap(List<int> results, int index1, int index2) {
        int temp = results[index1];
        results[index1] = results[index2];
        results[index2] = temp;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
    def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
        m, n = len(matrix), len(matrix[0])
        pre = [[0] * (n + 1) for _ in range(m + 1)]
        results = list()
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1]
                results.append(pre[i][j])
        
        def nth_element(left: int, kth: int, right: int, op: Callable[[int, int], bool]):
            if left == right:
                return
            
            pivot = random.randint(left, right)
            results[pivot], results[right] = results[right], results[pivot]

            # 三路划分（three-way partition）
            sepl = sepr = left - 1
            for i in range(left, right + 1):
                if op(results[i], results[right]):
                    sepr += 1
                    if sepr != i:
                        results[sepr], results[i] = results[i], results[sepr]
                    sepl += 1
                    if sepl != sepr:
                        results[sepl], results[sepr] = results[sepr], results[sepl]
                elif results[i] == results[right]:
                    sepr += 1
                    if sepr != i:
                        results[sepr], results[i] = results[i], results[sepr]
            
            if sepl < left + kth <= sepr:
                return
            elif left + kth <= sepl:
                nth_element(left, kth, sepl, op)
            else:
                nth_element(sepr + 1, kth - (sepr - left + 1), right, op)

        nth_element(0, k - 1, len(results) - 1, operator.gt)
        return results[k - 1]
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func quickSelect(a []int, k int) int {
    rand.Shuffle(len(a), func(i, j int) { a[i], a[j] = a[j], a[i] })
    for l, r := 0, len(a)-1; l < r; {
        v := a[l]
        i, j := l, r+1
        for {
            for i++; i < r && a[i] < v; i++ {
            }
            for j--; j > l && a[j] > v; j-- {
            }
            if i >= j {
                break
            }
            a[i], a[j] = a[j], a[i]
        }
        a[l], a[j] = a[j], v
        if j == k {
            break
        } else if j < k {
            l = j + 1
        } else {
            r = j - 1
        }
    }
    return a[k]
}

func kthLargestValue(matrix [][]int, k int) int {
    m, n := len(matrix), len(matrix[0])
    results := make([]int, 0, m*n)
    pre := make([][]int, m+1)
    pre[0] = make([]int, n+1)
    for i, row := range matrix {
        pre[i+1] = make([]int, n+1)
        for j, val := range row {
            pre[i+1][j+1] = pre[i+1][j] ^ pre[i][j+1] ^ pre[i][j] ^ val
            results = append(results, pre[i+1][j+1])
        }
    }
    return quickSelect(results, m*n-k)
}
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
void swap(int* a, int* b) {
    int t = *a;
    *a = *b, *b = t;
}

int cmp(int a, int b) {
    return a > b;
}

void nth_element(int* arr, int left, int kth, int right) {
    if (left == right) {
        return;
    }
    int pivot = left + rand() % (right - left);
    swap(&arr[pivot], &arr[right]);
    // 三路划分（three-way partition）
    int sepl = left - 1, sepr = left - 1;
    for (int i = left; i <= right; i++) {
        if (arr[i] > arr[right]) {
            swap(&arr[++sepr], &arr[i]);
            swap(&arr[++sepl], &arr[sepr]);
        } else if (arr[i] == arr[right]) {
            swap(&arr[++sepr], &arr[i]);
        }
    }
    if (sepl < left + kth && left + kth <= sepr) {
        return;
    } else if (left + kth <= sepl) {
        nth_element(arr, left, kth, sepl);
    } else {
        nth_element(arr, sepr + 1, kth - (sepr - left + 1), right);
    }
}

int kthLargestValue(int** matrix, int matrixSize, int* matrixColSize, int k) {
    int m = matrixSize, n = matrixColSize[0];
    int pre[m + 1][n + 1];
    memset(pre, 0, sizeof(pre));
    int results[m * n], resultsSize = 0;
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
            results[resultsSize++] = pre[i][j];
        }
    }
    nth_element(results, 0, k - 1, resultsSize - 1);
    return results[k - 1];
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
var kthLargestValue = function(matrix, k) {
    const m = matrix.length, n = matrix[0].length;
    const pre = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    const results = [];
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
            results.push(pre[i][j]);
        }
    }
    nthElement(results, 0, k - 1, results.length - 1);
    return results[k - 1];
}

const nthElement = (results, left, kth, right) => {
    if (left === right) {
        return;
    }
    const pivot = parseInt(Math.random() * (right - left) + left);
    swap(results, pivot, right);
    // 三路划分（three-way partition）
    let sepl = left - 1, sepr = left - 1;
    for (let i = left; i <= right; i++) {
        if (results[i] > results[right]) {
            swap(results, ++sepr, i);
            swap(results, ++sepl, sepr);
        } else if (results[i] === results[right]) {
            swap(results, ++sepr, i);
        }
    }
    if (sepl < left + kth && left + kth <= sepr) {
        return;
    } else if (left + kth <= sepl) {
        nthElement(results, left, kth, sepl);
    } else {
        nthElement(results, sepr + 1, kth - (sepr - left + 1), right);
    }
}

const swap = (results, index1, index2) => {
    const temp = results[index1];
    results[index1] = results[index2];
    results[index2] = temp;
}

复杂度分析

  • 时间复杂度：O(mn)。计算二维前缀和的时间复杂度为 O(mn)，快速选择找出第 k 大的元素的期望时间复杂度为 O(mn)，最坏情况下时间复杂度为 O((mn)^2)，因此总时间复杂度为 O(mn)。

  • 空间复杂度：O(mn)，即为存储二维前缀和需要的空间。

✨扣友帮帮团 - 互动答疑

讨论.jpg{:width=260px}

即日起 - 5 月 30 日，点击 这里  前往「扣友帮帮团 」活动页，把你遇到的问题大胆地提出来，让扣友为你解答～

🎁 奖励规则

被采纳数量排名 1～3 名：「力扣极客套装」 *1 并将获得「力扣神秘应援团」内测资格
被采纳数量排名 4～10 名：「力扣鼠标垫」 *1 并将获得「力扣神秘应援团」内测资格
「诲人不倦」：活动期间「解惑者」只要有 1 个回答被采纳，即可获得 20 LeetCoins 奖励！
「求知若渴」：活动期间「求知者」在活动页发起一次符合要求的疑问帖并至少采纳一次「解惑者」的回答，即可获得 20 LeetCoins 奖励！

活动详情猛戳链接了解更多：活动｜你有 BUG 我来帮 - 力扣互动答疑季

 Comments
On this page
1738-找出第 K 大的异或坐标值
  1. ✨扣友帮帮团 - 互动答疑
    1. 🎁 奖励规则