1751-最多可以参加的会议数目 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

给你一个 events 数组，其中 events[i] = [startDayi, endDayi, valuei] ，表示第 i 个会议在
startDayi 天开始，第 endDayi 天结束，如果你参加这个会议，你能得到价值 valuei 。同时给你一个整数 k
表示你能参加的最多会议数目。

你同一时间只能参加一个会议。如果你选择参加某个会议，那么你必须 完整
地参加完这个会议。会议结束日期是包含在会议内的，也就是说你不能同时参加一个开始日期与另一个结束日期相同的两个会议。

请你返回能得到的会议价值 最大和 。

示例 1：

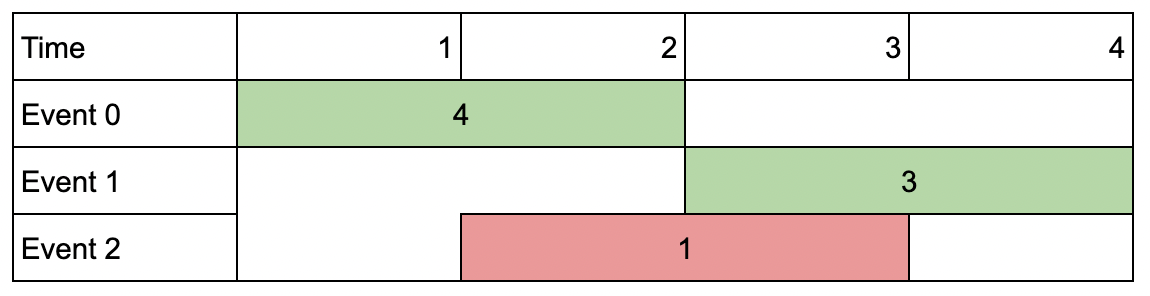
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/02/06/screenshot-2021-01-11-at-60048-pm.png)

**输入：** events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
**输出：** 7
**解释：** 选择绿色的活动会议 0 和 1，得到总价值和为 4 + 3 = 7 。

示例 2：

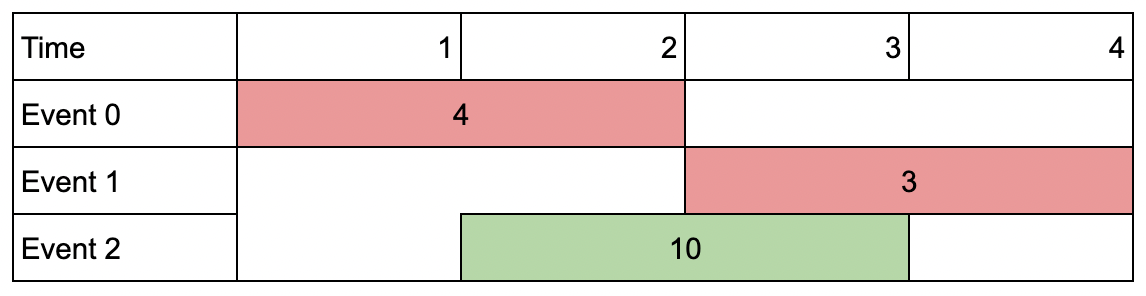
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/02/06/screenshot-2021-01-11-at-60150-pm.png)

**输入：** events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
**输出：** 10
**解释：** 参加会议 2 ，得到价值和为 10 。
你没法再参加别的会议了，因为跟会议 2 有重叠。你 **不** 需要参加满 k 个会议。

示例 3：

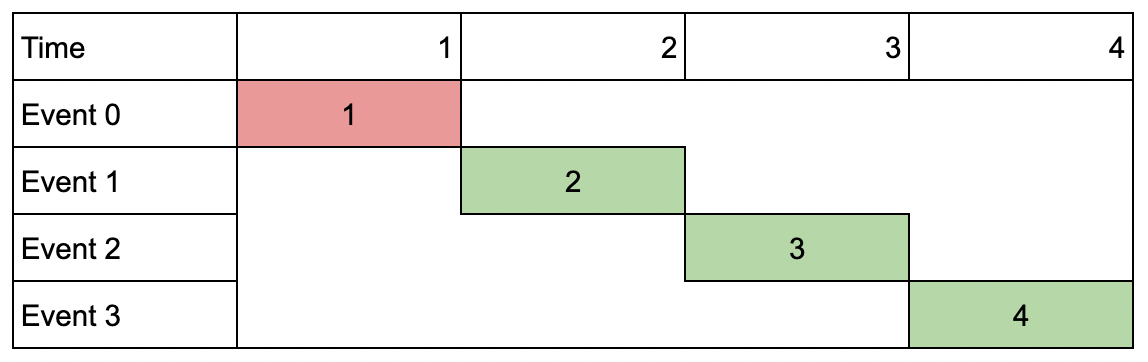
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/02/06/screenshot-2021-01-11-at-60703-pm.png)

**输入：** events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
**输出：** 9
**解释：** 尽管会议互不重叠，你只能参加 3 个会议，所以选择价值最大的 3 个会议。

提示：

  • 1 <= k <= events.length
  • 1 <= k * events.length <= 106
  • 1 <= startDayi <= endDayi <= 109
  • 1 <= valuei <= 106

按照结束时间排序。

定义 f[i][j] 表示参加前 i 个会议中的至多 j 个，能得到的会议价值的最大和。

分类讨论：

  • 不参加第 i 个会议：f[i][j] = f[i-1][j]；
  • 参加第 i 个会议：f[i][j] = f[p][j-1] + \textit{value}[i]，其中 p 是最大的满足 endDay}[p]<\textit{startDay}[i] 的 p，不存在时为 -1。

两者取最大值，即

f[i][j] = \max(f[i-1][j],f[p][j-1] + \textit{value}[i])

代码实现时，为避免处理 -1，可将与 f 有关的下标都 +1，即

f[i+1][j] = \max(f[i][j], f[p+1][j-1]+\textit{value}[i])

答案为 f[n][k]。

代码实现时，由于结束时间是有序的，p 可以用二分查找计算出来。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def maxValue(self, events: List[List[int]], k: int) -> int:
        events.sort(key=lambda e: e[1])
        n = len(events)
        f = [[0] * (k + 1) for _ in range(n + 1)]
        for i, (start, end, val) in enumerate(events):
            p = bisect_left(events, start, hi=i, key=lambda e: e[1])  # hi=i 表示二分上界为 i（默认为 n）
            for j in range(1, k + 1):
                # 为什么是 p 不是 p+1：上面算的是 >= start，-1 后得到 < start，但由于还要 +1，抵消了
                f[i + 1][j] = max(f[i][j], f[p][j - 1] + val)
        return f[n][k]
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int maxValue(int[][] events, int k) {
        Arrays.sort(events, (a, b) -> a[1] - b[1]); // 按照结束时间排序
        var n = events.length;
        var f = new int[n + 1][k + 1];
        for (var i = 0; i < n; ++i) {
            var p = search(events, i, events[i][0]);
            for (var j = 1; j <= k; ++j)
                f[i + 1][j] = Math.max(f[i][j], f[p + 1][j - 1] + events[i][2]);
        }
        return f[n][k];
    }

    // 返回 endDay < upper 的最大下标
    private int search(int[][] events, int right, int upper) {
        var left = -1;
        while (left + 1 < right) {
            var mid = (left + right) / 2;
            if (events[mid][1] < upper) left = mid;
            else right = mid;
        }
        return left;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxValue(vector<vector<int>> &events, int k) {
        sort(events.begin(), events.end(), [](auto &a, auto &b) { return a[1] < b[1]; }); // 按照结束时间排序
        int n = events.size(), f[n + 1][k + 1];
        memset(f, 0, sizeof(f));
        for (int i = 0; i < n; ++i) {
            int p = lower_bound(events.begin(), events.begin() + i, events[i][0],
                                [](auto &e, int lower) { return e[1] < lower; }) - events.begin();
            for (int j = 1; j <= k; ++j)
                // 为什么是 p 不是 p+1：上面算的是 >= events[i][0]，-1 后得到 < events[i][0]，但由于还要 +1，抵消了
                f[i + 1][j] = max(f[i][j], f[p][j - 1] + events[i][2]);
        }
        return f[n][k];
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func maxValue(events [][]int, k int) int {
	sort.Slice(events, func(i, j int) bool { return events[i][1] < events[j][1] }) // 按照结束时间排序
	n := len(events)
	f := make([][]int, n+1)
	for i := range f {
		f[i] = make([]int, k+1)
	}
	for i, e := range events {
		p := sort.Search(i, func(j int) bool { return events[j][1] >= e[0] })
		for j := 1; j <= k; j++ {
			// 为什么是 p 不是 p+1：上面算的是 >= e[0]，-1 后得到 < e[0]，但由于还要 +1，抵消了
			f[i+1][j] = max(f[i][j], f[p][j-1]+e[2])
		}
	}
	return f[n][k]
}

func max(a, b int) int { if b > a { return b }; return a }

编程小课堂 · 标准库二分的灵活运用

在写二分题目时，经常会遇到形如「在有序数组中查询大于某个数的最小数」这类问题。具体来说有四类：

  • \ge：在有序数组中查询大于或等于某个数的最小数；

  • ：在有序数组中查询大于某个数的最小数；

  • \le：在有序数组中查询小于或等于某个数的最大数；
  • <：在有序数组中查询小于某个数的最大数。

上面的 Python/C++/Go 代码都中用到了标准库中的二分，但这些二分在设计的时候，只提供了查询 \ge 和 > 的功能，并没有提供查询 \le 和 < 的功能。

没有关系，稍微转换下就能解决。比如查询 \ge 得到了下标 i，那么 i-1 就是 < 的结果了（假设数组为升序），同理 \le 可以用 > 算出来。

注：> 和 \ge 也可以转换，对于整数来说，> x 等价于 \ge x+1。

复杂度分析

  • 时间复杂度：O(nk+n\log n)，其中 n 为 events 的长度。
  • 空间复杂度：O(nk)。

相似题目

欢迎关注我的B站频道：灵茶山艾府 ，每周更新算法讲解视频哦~

 Comments
On this page
1751-最多可以参加的会议数目 II