1786-从第一个节点出发到最后一个节点的受限路径数
现有一个加权无向连通图。给你一个正整数 n ,表示图中有 n 个节点,并按从 1 到 n 给节点编号;另给你一个数组 edges
,其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边,这条边的权重为weighti 。
从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, ..., zk] 的节点序列,满足 z0 = start
、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。
路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。
受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径,其中 0 <= i <= k-1 。
返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大,请返回对 109 + 7 取余 的结果。
示例 1:
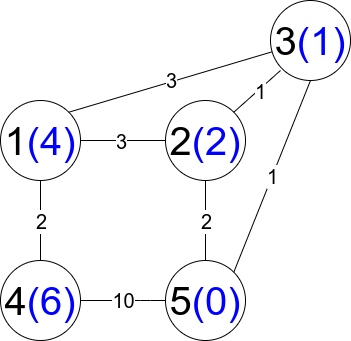
**输入:** n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
**输出:** 3
**解释:** 每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5
示例 2:
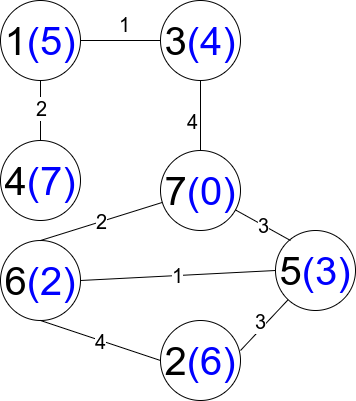
**输入:** n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
**输出:** 1
**解释:** 每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。唯一一条受限路径是:1 --> 3 --> 7 。
提示:
1 <= n <= 2 * 104n - 1 <= edges.length <= 4 * 104edges[i].length == 31 <= ui, vi <= nui != vi1 <= weighti <= 105- 任意两个节点之间至多存在一条边
- 任意两个节点之间至少存在一条路径

- 跑一遍堆优化Dijkstra,求出所有点到n的最短距离
- 动态规划,定义
dp[i]表示从 1 -> i 受限制的路径数,由于动态规划要求无后效性,如果dist[i] > dist[j],则dp[j]一定可以从dp[i]转移过来,dp[i]一定不能从dp[j]转移过来,因此需要对所有节点按dist从大到小(或者从小到大)排序 - 对于某个结点 i,则和它相连的点 j,如果
dist[j] < dist[i], 则i->j可行,因此,dp[j] += dp[i]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58class Solution {
private:
typedef long long LL;
typedef pair<int, int> PII;
static const int N = 2e4 + 10, M = 8e4 + 10, MOD = 1e9 + 7;
int h[N], e[M], w[M], ne[M], idx = 0;
LL dist[N];
bool st[N];
int n;
void add(int a, int b, int wt) {
e[idx] = b, w[idx] = wt, ne[idx] = h[a], h[a] = idx++;
}
void dijkstra() {
memset(dist, 0x3f, sizeof dist);
memset(st, false, sizeof st);
dist[n] = 0;
priority_queue<PII, vector<PII>, greater<>> heap;
heap.emplace(0, n);
while (heap.size()) {
auto t = heap.top();
heap.pop();
int ver = t.second, wt = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > wt + w[i]) {
dist[j] = wt + w[i];
heap.emplace(dist[j], j);
}
}
}
}
public:
int countRestrictedPaths(int n, vector<vector<int>>& edges) {
this->n = n;
memset(h, -1, sizeof h);
for (auto& e : edges) {
int a = e[0], b = e[1], wt = e[2];
add(a, b, wt), add(b, a, wt);
}
dijkstra();
LL dp[n + 1]; // dp[i] 表示从1->i受限制的路径数
memset(dp, 0, sizeof dp);
dp[1] = 1;
int id[n + 1];
for (int i = 1; i <= n; i++) id[i] = i;
sort(id + 1, id + n + 1, [&](int i, int j){return dist[i] > dist[j];});
for (int i = 1; i <= n; i++) {
int u = id[i];
for (int k = h[u]; k != -1; k = ne[k]) {
int j = e[k];
if (dist[u] > dist[j]) dp[j] = (dp[j] + dp[u]) % MOD;
}
}
return dp[n];
}
};
Comments