1823-找出游戏的获胜者

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i
名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1
名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置开始。
沿着顺时针方向数 k 名小伙伴，计数时需要包含起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。

给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：

**输入：** n = 5, k = 2
**输出：** 3
**解释：** 游戏运行步骤如下：
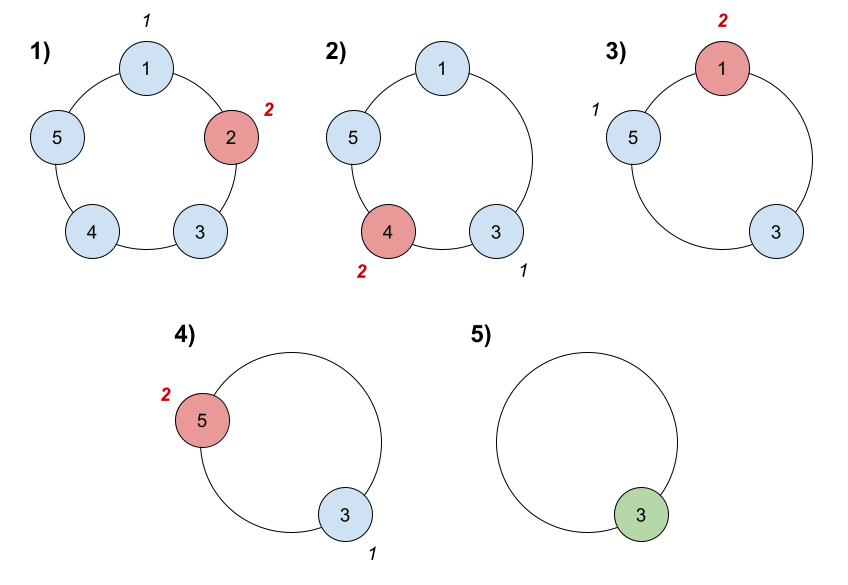
1) 从小伙伴 1 开始。
2) 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6) 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

**输入：** n = 6, k = 5
**输出：** 1
**解释：** 小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示：

1 <= k <= n <= 500

进阶： 你能否使用线性时间复杂度和常数空间复杂度解决此问题？

方法一：模拟 + 队列

最直观的方法是模拟游戏过程。使用队列存储圈子中的小伙伴编号，初始时将 1 到 n 的所有编号依次加入队列，队首元素即为第 1 名小伙伴的编号。

每一轮游戏中，从当前小伙伴开始数 k 名小伙伴，数到的第 k 名小伙伴离开圈子。模拟游戏过程的做法是，将队首元素取出并将该元素在队尾处重新加入队列，重复该操作 k - 1 次，则在 k - 1 次操作之后，队首元素即为这一轮中数到的第 k 名小伙伴的编号，将队首元素取出，即为数到的第 k 名小伙伴离开圈子。上述操作之后，新的队首元素即为下一轮游戏的起始小伙伴的编号。

每一轮游戏之后，圈子中减少一名小伙伴，队列中减少一个元素。重复上述过程，直到队列中只剩下 1 个元素，该元素即为获胜的小伙伴的编号。

[sol1-Python3]class Solution:
    def findTheWinner(self, n: int, k: int) -> int:
        q = deque(range(1, n + 1))
        while len(q) > 1:
            for _ in range(k - 1):
                q.append(q.popleft())
            q.popleft()
        return q[0]

[sol1-Java]class Solution {
    public int findTheWinner(int n, int k) {
        Queue<Integer> queue = new ArrayDeque<Integer>();
        for (int i = 1; i <= n; i++) {
            queue.offer(i);
        }
        while (queue.size() > 1) {
            for (int i = 1; i < k; i++) {
                queue.offer(queue.poll());
            }
            queue.poll();
        }
        return queue.peek();
    }
}

[sol1-C#]public class Solution {
    public int FindTheWinner(int n, int k) {
        Queue<int> queue = new Queue<int>();
        for (int i = 1; i <= n; i++) {
            queue.Enqueue(i);
        }
        while (queue.Count > 1) {
            for (int i = 1; i < k; i++) {
                queue.Enqueue(queue.Dequeue());
            }
            queue.Dequeue();
        }
        return queue.Peek();
    }
}

[sol1-C++]class Solution {
public:
    int findTheWinner(int n, int k) {
        queue<int> qu;
        for (int i = 1; i <= n; i++) {
            qu.emplace(i);
        }
        while (qu.size() > 1) {
            for (int i = 1; i < k; i++) {
                qu.emplace(qu.front());
                qu.pop();
            }
            qu.pop();
        }
        return qu.front();
    }
};

[sol1-C]int findTheWinner(int n, int k){
    struct ListNode * head = NULL;
    struct ListNode * tail = NULL;
    for (int i = 1; i <= n; i++) {
        struct ListNode * node = (struct ListNode *)malloc(sizeof(struct ListNode));
        node->val = i;
        node->next = NULL;
        if (!head) {
            head = node;
            tail = node;
        } else {
            tail->next = node;
            tail = tail->next;
        }
    }
    while (head != tail) {
        for (int i = 1; i < k; i++) {
            struct ListNode * node = head;
            head = head->next;
            tail->next = node;
            tail = tail->next;
            tail->next = NULL;
        }
        struct ListNode * node = head;
        head = head->next;
        free(node);
    }
    int res = head->val;
    free(head);
    return res;
}

[sol1-JavaScript]var findTheWinner = function(n, k) {
    const queue = [];
    for (let i = 1; i <= n; i++) {
        queue.push(i);
    }
    while (queue.length > 1) {
        for (let i = 1; i < k; i++) {
            queue.push(queue.shift());
        }
        queue.shift();
    }
    return queue[0];
};

[sol1-Golang]func findTheWinner(n, k int) int {
    q := make([]int, n)
    for i := range q {
        q[i] = i + 1
    }
    for len(q) > 1 {
        for i := 1; i < k; i++ {
            q = append(q, q[0])[1:]
        }
        q = q[1:]
    }
    return q[0]
}

复杂度分析

时间复杂度：O(nk)，其中 n 是做游戏的小伙伴数量，k 是每一轮离开圈子的小伙伴的计数。初始时需要将 n 个元素加入队列，每一轮需要将 k 个元素从队列中取出，将 k - 1 个元素加入队列，一共有 n - 1 轮，因此时间复杂度是 O(nk)。
空间复杂度：O(n)，其中 n 是做游戏的小伙伴数量。空间复杂度主要取决于队列，队列中最多有 n 个元素。

方法二：数学 + 递归

以下用 f(n, k) 表示 n 名小伙伴做游戏，每一轮离开圈子的小伙伴的计数为 k 时的获胜者编号。

当 n = 1 时，圈子中只有一名小伙伴，该小伙伴即为获胜者，因此 f(1, k) = 1。

当 n > 1 时，将有一名小伙伴离开圈子，圈子中剩下 n - 1 名小伙伴。圈子中的第 k’ 名小伙伴离开圈子，k’ 满足 1 \le k’ \le n 且 k - k’ 是 n 的倍数。

由于 1 \le k’ \le n，因此 0 \le k’ - 1 \le n - 1。又由于 k - k’ 是 n 的倍数等价于 (k - 1) - (k’ - 1) 是 n 的倍数，因此 k’ - 1 = (k - 1) \bmod n，k’ = (k - 1) \bmod n + 1。

当圈子中剩下 n - 1 名小伙伴时，可以递归地计算 f(n - 1, k)，得到剩下的 n - 1 名小伙伴中的获胜者。令 x = f(n - 1, k)。

由于在第 k’ 名小伙伴离开圈子之后，圈子中剩下的 n - 1 名小伙伴从第 k’ + 1 名小伙伴开始计数，获胜者编号是从第 k’ + 1 名小伙伴开始的第 x 名小伙伴，因此当圈子中有 n 名小伙伴时，获胜者编号是 f(n, k) = (k’ \bmod n + x - 1) \bmod n + 1 = (k + x - 1) \bmod n + 1。

将 x = f(n - 1, k) 代入上述关系，可得：f(n, k) = (k + f(n - 1, k) - 1) \bmod n + 1。

[sol2-Python3]class Solution:
    def findTheWinner(self, n: int, k: int) -> int:
        return 1 if n == 1 else (k + self.findTheWinner(n - 1, k) - 1) % n + 1

[sol2-Java]class Solution {
    public int findTheWinner(int n, int k) {
        if (n == 1) {
            return 1;
        }
        return (k + findTheWinner(n - 1, k) - 1) % n + 1;
    }
}

[sol2-C#]public class Solution {
    public int FindTheWinner(int n, int k) {
        if (n == 1) {
            return 1;
        }
        return (k + FindTheWinner(n - 1, k) - 1) % n + 1;
    }
}

[sol2-C++]class Solution {
public:
    int findTheWinner(int n, int k) {
        if (n == 1) {
            return 1;
        }
        return (k + findTheWinner(n - 1, k) - 1) % n + 1;
    }
};

[sol2-C]int findTheWinner(int n, int k){
    if (n == 1) {
        return 1;
    }
    return (k + findTheWinner(n - 1, k) - 1) % n + 1;
}

[sol2-JavaScript]var findTheWinner = function(n, k) {
    if (n === 1) {
        return 1;
    }
    return (k + findTheWinner(n - 1, k) - 1) % n + 1;
};

[sol2-Golang]func findTheWinner(n, k int) int {
    if n == 1 {
        return 1
    }
    return (k+findTheWinner(n-1, k)-1)%n + 1
}

复杂度分析

时间复杂度：O(n)，其中 n 是做游戏的小伙伴数量。需要计算的值有 n 个，每个值的计算时间都是 O(1)。
空间复杂度：O(n)，其中 n 是做游戏的小伙伴数量。空间复杂度主要取决于递归调用栈的深度，为 O(n) 层。

方法三：数学 + 迭代

方法二的递归实现可以改成迭代实现，省略递归调用栈空间。

[sol3-Python3]class Solution:
    def findTheWinner(self, n: int, k: int) -> int:
        winner = 1
        for i in range(2, n + 1):
            winner = (k + winner - 1) % i + 1
        return winner

[sol3-Java]class Solution {
    public int findTheWinner(int n, int k) {
        int winner = 1;
        for (int i = 2; i <= n; i++) {
            winner = (k + winner - 1) % i + 1;
        }
        return winner;
    }
}

[sol3-C#]public class Solution {
    public int FindTheWinner(int n, int k) {
        int winner = 1;
        for (int i = 2; i <= n; i++) {
            winner = (k + winner - 1) % i + 1;
        }
        return winner;
    }
}

[sol3-C++]class Solution {
public:
    int findTheWinner(int n, int k) {
        int winner = 1;
        for (int i = 2; i <= n; i++) {
            winner = (k + winner - 1) % i + 1;
        }
        return winner;
    }
};

[sol3-C]int findTheWinner(int n, int k){
    int winner = 1;
    for (int i = 2; i <= n; i++) {
        winner = (k + winner - 1) % i + 1;
    }
    return winner;
}

[sol3-JavaScript]var findTheWinner = function(n, k) {
    let winner = 1;
    for (let i = 2; i <= n; i++) {
        winner = (k + winner - 1) % i + 1;
    }
    return winner;
};

[sol3-Golang]func findTheWinner(n, k int) int {
    winner := 1
    for i := 2; i <= n; i++ {
        winner = (k+winner-1)%i + 1
    }
    return winner
}

复杂度分析

时间复杂度：O(n)，其中 n 是做游戏的小伙伴数量。需要 O(n) 的时间遍历并计算结果。
空间复杂度：O(1)。