给你一个长度为 n 的 3 跑道道路 ,它总共包含 n + 1 个 点 ,编号为 0 到 n 。一只青蛙从 0
号点第二条跑道 出发 ,它想要跳到点 n 处。然而道路上可能有一些障碍。
给你一个长度为 n + 1 的数组 obstacles ,其中 obstacles[i] ( 取值范围从 0 到 3 )表示在点 i
处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ,那么点 i 处没有障碍。任何一个点的三条跑道中
最多有一个 障碍。
- 比方说,如果
obstacles[2] == 1 ,那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍,这只青蛙也可以在 同一个
点处 侧跳 到 另外一条 跑道(这两条跑道可以不相邻),但前提是跳过去的跑道该点处没有障碍。
- 比方说,这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2 出发,并想到达点 n 处的 任一跑道 ,请你返回 最少侧跳次数 。
注意 :点 0 处和点 n 处的任一跑道都不会有障碍。
示例 1:

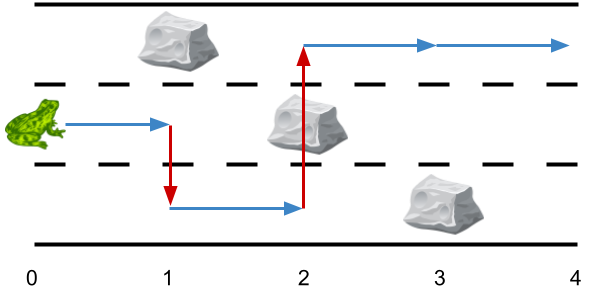
**输入:** obstacles = [0,1,2,3,0]
**输出:** 2
**解释:** 最优方案如上图箭头所示。总共有 2 次侧跳(红色箭头)。
注意,这只青蛙只有当侧跳时才可以跳过障碍(如上图点 2 处所示)。
示例 2:

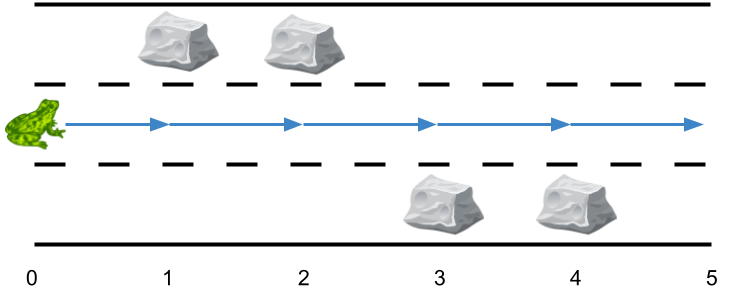
**输入:** obstacles = [0,1,1,3,3,0]
**输出:** 0
**解释:** 跑道 2 没有任何障碍,所以不需要任何侧跳。
示例 3:

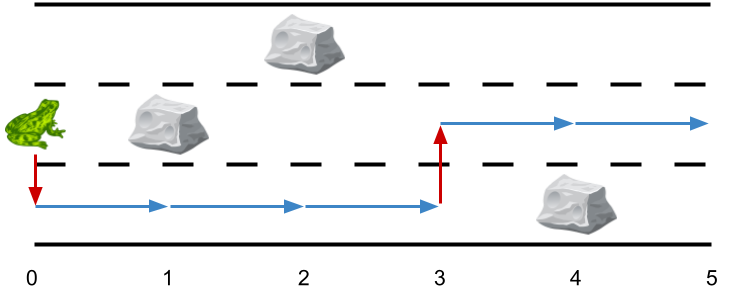
**输入:** obstacles = [0,2,1,0,3,0]
**输出:** 2
**解释:** 最优方案如上图所示。总共有 2 次侧跳。
提示:
obstacles.length == n + 11 <= n <= 5 * 1050 <= obstacles[i] <= 3obstacles[0] == obstacles[n] == 0
方法一:动态规划
思路与算法
为了方便编写代码,我们用 0,1,2 对跑道进行编号,因此 obstacles}[i] 减去 1 后与跑道对应,其等于 -1 时表示该点没有障碍。
我们可以使用动态规划来解决本题,设 d[i][j] 表示青蛙到达 i 号点的 j 号跑道时所需要的最少侧跳次数。
初始时,青蛙处于 0 号点的 1 号跑道,因此 d[0][1] = 0。又由于题目保证点 0 处没有障碍,并且青蛙可以通过一次侧跳到达其他跑道,所以 d[0][0] 与 d[0][2] 初始值都为 1。对于其他状态的默认值我们设置为正无穷。
转移时,我们分两步考虑:
首先,青蛙可以从点 i - 1 处直接跳到点 i 处,前提是当前跑道没有障碍,如果有障碍,我们需要单独将其设置为正无穷。因此,有如下转移方程:
d[i][j] =
\begin{cases}
d[i - 1][j] & j \neq \textit{obstacles}[i] - 1 \
\inf & j = \textit{obstacles}[i] - 1
\end{cases}
其中 j \in [0, 2]。
然后,青蛙可以通过消耗一次侧跳次数从点 i 处的其他跑道跳到当前跑道。我们设 minCnt} = \min(d[i][0], d[i][1], d[i][2]),然后尝试用 minCnt} + 1 来更新每个 d[i][j]。因此,有如下转移方程:
d[i][j] = \min(d[i][j], minCnt + 1)
其中 j \in [0, 2],且 j \neq \textit{obstacles}[i] - 1。
经过 n 次转移后, \min(d[n][0], d[n][1], d[n][2]) 就是答案。
我们不难通过上述转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n) 的实现,但是由于 d[i] 求解时只利用到了 d[i-1],并且通过转移方程我们可以发现额外存储 d[i - 1] 是没有必要的。因此,可以利用「滚动数组思想」把空间复杂度优化为 O(1),在本题中,只需要用一个长度为 3 的数组即可。
代码
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution:
def minSideJumps(self, obstacles: List[int]) -> int:
d = [1, 0, 1]
for i in range(1, len(obstacles)):
minCnt = inf
for j in range(3):
if j == obstacles[i] - 1:
d[j] = inf
else:
minCnt = min(minCnt, d[j])
for j in range(3):
if j != obstacles[i] - 1:
d[j] = min(d[j], minCnt + 1)
return min(d)
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
static constexpr int inf = 0x3f3f3f3f;
public:
int minSideJumps(vector<int> &obstacles) {
int n = obstacles.size() - 1;
vector<int> d = {1, 0, 1};
for (int i = 1; i <= n; i++) {
int minCnt = inf;
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
d[j] = inf;
} else {
minCnt = min(minCnt, d[j]);
}
}
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
continue;
}
d[j] = min(d[j], minCnt + 1);
}
}
return *min_element(d.begin(), d.end());
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
static final int INF = 0x3fffffff;
public int minSideJumps(int[] obstacles) {
int n = obstacles.length - 1;
int[] d = new int[3];
Arrays.fill(d, 1);
d[1] = 0;
for (int i = 1; i <= n; i++) {
int minCnt = INF;
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
d[j] = INF;
} else {
minCnt = Math.min(minCnt, d[j]);
}
}
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
continue;
}
d[j] = Math.min(d[j], minCnt + 1);
}
}
return Math.min(Math.min(d[0], d[1]), d[2]);
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public class Solution {
const int INF = 0x3fffffff;
public int MinSideJumps(int[] obstacles) {
int n = obstacles.Length - 1;
int[] d = new int[3];
Array.Fill(d, 1);
d[1] = 0;
for (int i = 1; i <= n; i++) {
int minCnt = INF;
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
d[j] = INF;
} else {
minCnt = Math.Min(minCnt, d[j]);
}
}
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
continue;
}
d[j] = Math.Min(d[j], minCnt + 1);
}
}
return Math.Min(Math.Min(d[0], d[1]), d[2]);
}
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| const int INF = 0X3f3f3f3f;
static inline int min(int a, int b) {
return a < b ? a : b;
}
int minSideJumps(int* obstacles, int obstaclesSize) {
int d[3] = {1, 0, 1};
for (int i = 1; i < obstaclesSize; i++) {
int minCnt = INF;
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
d[j] = INF;
} else {
minCnt = min(minCnt, d[j]);
}
}
for (int j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
continue;
}
d[j] = min(d[j], minCnt + 1);
}
}
return min(d[0], min(d[1], d[2]));
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| var minSideJumps = function(obstacles) {
const n = obstacles.length - 1;
const d = [1, 0, 1];
for (let i = 1; i <= n; i++) {
let minCnt = Number.MAX_VALUE;
for (let j = 0; j < 3; j++) {
if (j === obstacles[i] - 1) {
d[j] = Number.MAX_VALUE;
} else {
minCnt = Math.min(minCnt, d[j]);
}
}
for (let j = 0; j < 3; j++) {
if (j == obstacles[i] - 1) {
continue;
}
d[j] = Math.min(d[j], minCnt + 1);
}
}
return _.min([d[0], d[1], d[2]]);
};
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| func minSideJumps(obstacles []int) int {
d := [3]int{1, 0, 1}
for _, x := range obstacles[1:] {
minCnt := math.MaxInt / 2
for j := 0; j < 3; j++ {
if j == x-1 {
d[j] = math.MaxInt / 2
} else {
minCnt = min(minCnt, d[j])
}
}
for j := 0; j < 3; j++ {
if j != x-1 {
d[j] = min(d[j], minCnt+1)
}
}
}
return min(min(d[0], d[1]), d[2])
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
|
复杂度分析