1839-所有元音按顺序排布的最长子字符串

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

当一个字符串满足如下条件时，我们称它是 美丽的 ：

  • 所有 5 个英文元音字母（'a' ，'e' ，'i' ，'o' ，'u'）都必须 至少 出现一次。
  • 这些元音字母的顺序都必须按照 字典序 升序排布（也就是说所有的 'a' 都在 'e' 前面，所有的 'e' 都在 'i' 前面，以此类推）

比方说，字符串 "aeiou" 和 "aaaaaaeiiiioou" 都是 美丽的 ，但是 "uaeio" ，"aeoiu" 和
"aaaeeeooo" 不是美丽的 。

给你一个只包含英文元音字母的字符串 word ，请你返回 word 中 最长美丽子字符串的长度 。如果不存在这样的子字符串，请返回 0
。

子字符串 是字符串中一个连续的字符序列。

示例 1：

**输入：** word = "aeiaaio **aaaaeiiiiouuu** ooaauuaeiu"
**输出：** 13
**解释：** 最长子字符串是 "aaaaeiiiiouuu" ，长度为 13 。

示例 2：

**输入：** word = "aeeeiiiioooauuu **aeiou** "
**输出：** 5
**解释：** 最长子字符串是 "aeiou" ，长度为 5 。

示例 3：

**输入：** word = "a"
**输出：** 0
**解释：** 没有美丽子字符串，所以返回 0 。

提示：

  • 1 <= word.length <= 5 * 105
  • word 只包含字符 'a'，'e'，'i'，'o' 和 'u' 。

方法一：状态机

提示 1

我们可以将 a,e,i,o,u 看成 5 个状态。
当我们在遍历字符串的每个字符时，都会处于其中的一个状态。如果当前在 u 状态，那么就可以对答案进行更新。

提示 2

你会如何设计状态之间的转移呢？

思路与算法

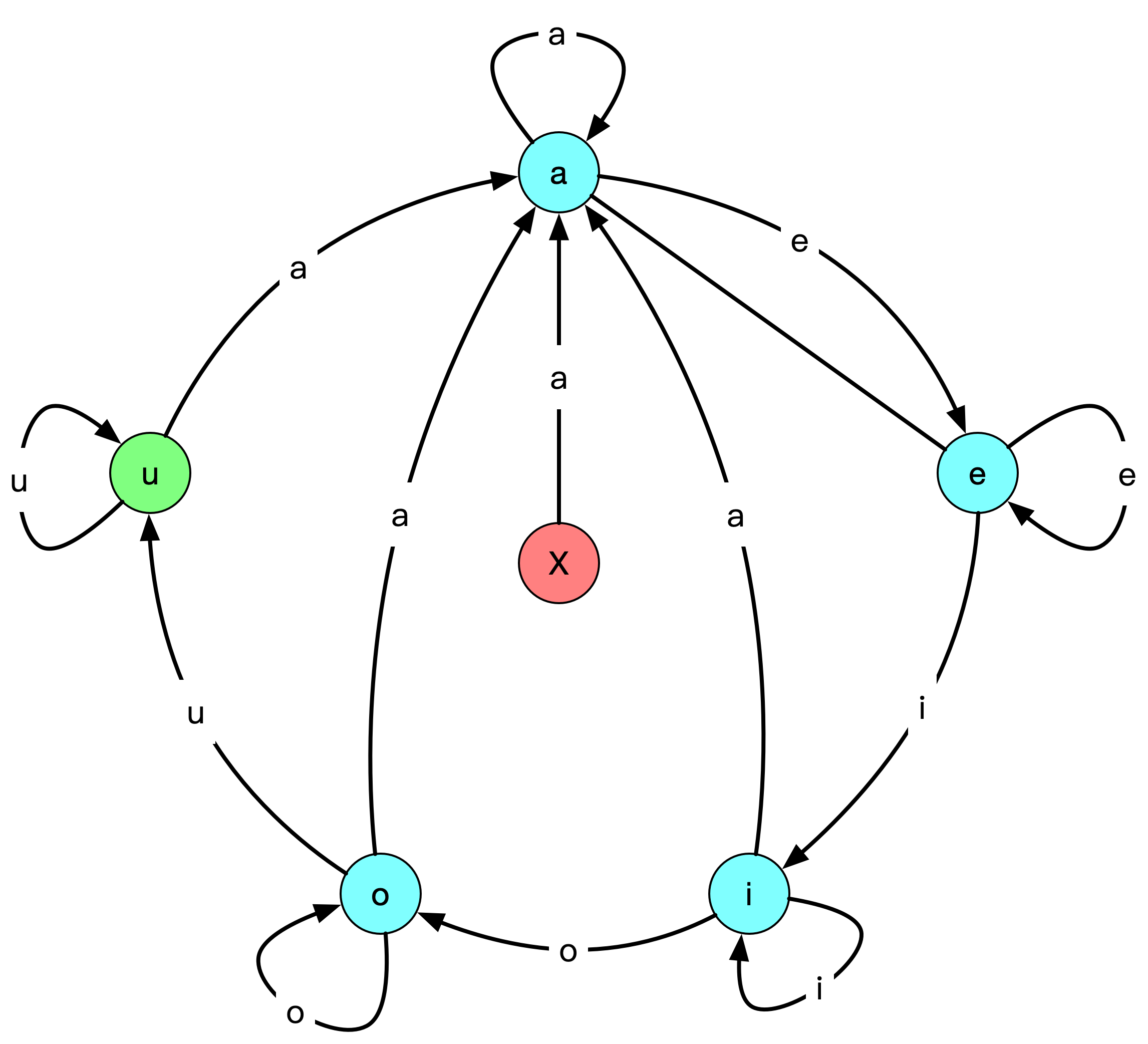
下面给出了状态转移图，其中蓝色的 a,e,i,o 表示正常状态，绿色的 u 表示目标状态，红色的 x 表示非法状态。

fig1{:style=”width:300px”}

图中也标注了两个状态之间的转移方式，对于没有标注的转移，一律转移到 x 非法状态。

这样一来，我们只需要从 x 状态开始，在对字符串进行一次遍历的同时，在状态机上进行转移即可。在转移的同时，我们需要记录到目前为止成功转移的次数 cnt，当到达 u 状态时，我们就可以用 cnt 来更新答案。

转移次数 cnt 的计算规则如下：

  • 当我们转移到 x 状态时，会将 cnt 清零；
  • 当我们转移到 a 状态时，如果上一个状态不为 a，那么会将 cnt 置为 1；
  • 对于其余的情况，将 cnt 增加 1 即可。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
private:
    static unordered_set<string> transit;

public:
    int longestBeautifulSubstring(string word) {
        int cur = 0, ans = 0;
        char status = 'x';
        
        for (char ch: word) {
            if (transit.count(string(1, status) + ch)) {
                if (status != 'a' && ch == 'a') {
                    cur = 1;
                }
                else {
                    ++cur;
                }
                status = ch;
            }
            else {
                cur = 0;
                status = 'x';
            }
            if (status == 'u') {
                ans = max(ans, cur);
            }
        }
        
        return ans;
    }
};

unordered_set<string> Solution::transit = {
    "ae", "ei", "io", "ou",
    "aa", "ee", "ii", "oo", "uu",
    "xa", "ea", "ia", "oa", "ua"
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:

    TRANSIT = {
        ("a", "e"), ("e", "i"), ("i", "o"), ("o", "u"),
        ("a", "a"), ("e", "e"), ("i", "i"), ("o", "o"), ("u", "u"),
        ("x", "a"), ("e", "a"), ("i", "a"), ("o", "a"), ("u", "a"),
    }
    
    def longestBeautifulSubstring(self, word: str) -> int:
        cur, ans = 0, 0
        status = "x"
        
        for ch in word:
            if (status, ch) in Solution.TRANSIT:
                if status != "a" and ch == "a":
                    cur = 1
                else:
                    cur = cur + 1
                status = ch
            else:
                cur = 0
                status = "x"
            if status == "u":
                ans = max(ans, cur)

        return ans

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 word 的长度。

  • 空间复杂度：O(|\Sigma|)，其中 \Sigma 是字符集，本体中给定的字符串仅包含元音字母，|\Sigma|=5。状态机中的转移分为三种：

    • 一个状态转移到本身，这种转移的数量为 O(|\Sigma|)；
    • 一个状态转移到相邻的下一个状态，例如 a 转移到 e，e 转移到 i，这种转移的数量为 O(|\Sigma|)；
    • 一个非 a 的状态转移到 a，这种转移的数量为 O(|\Sigma|)。

    因此转移的数量为 O(|\Sigma|)，即为我们需要的空间。

 Comments
On this page
1839-所有元音按顺序排布的最长子字符串