1840-最高建筑高度

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:15:46 2023-09-13 16:15:46 Updated    

在一座城市里，你需要建 n 栋新的建筑。这些新的建筑会从 1 到 n 编号排成一列。

这座城市对这些新建筑有一些规定：

  • 每栋建筑的高度必须是一个非负整数。
  • 第一栋建筑的高度 必须 是 0 。
  • 任意两栋相邻建筑的高度差 不能超过 1 。

除此以外，某些建筑还有额外的最高高度限制。这些限制会以二维整数数组 restrictions 的形式给出，其中 restrictions[i] = [idi, maxHeighti] ，表示建筑 idi 的高度 不能超过 maxHeighti 。

题目保证每栋建筑在 restrictions 中 至多出现一次 ，同时建筑 1 不会 出现在 restrictions 中。

请你返回 最高 建筑能达到的 最高高度 。

示例 1：

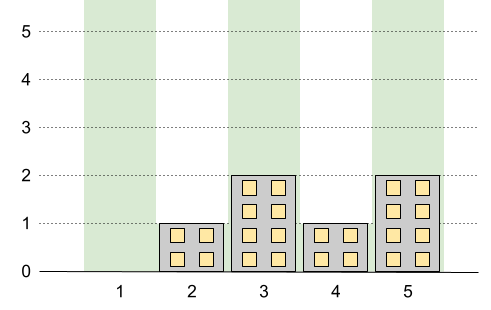
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/04/25/ic236-q4-ex1-1.png)

**输入：** n = 5, restrictions = [[2,1],[4,1]]
**输出：** 2
**解释：** 上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,1,2] ，最高建筑的高度为 2 。

示例 2：

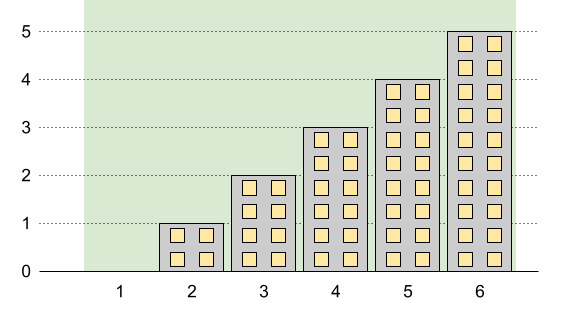
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/04/25/ic236-q4-ex2.png)

**输入：** n = 6, restrictions = []
**输出：** 5
**解释：** 上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,3,4,5] ，最高建筑的高度为 5 。

示例 3：

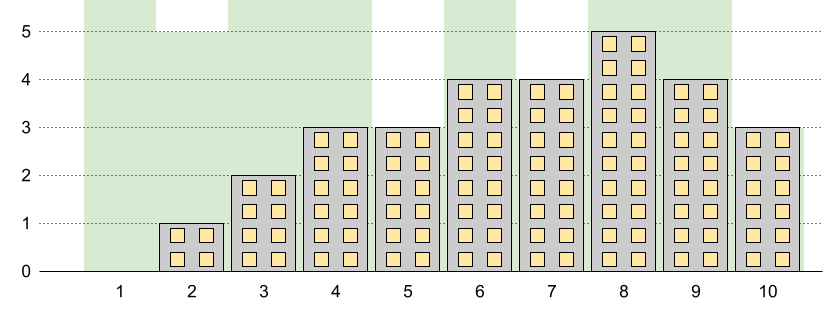
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2021/04/25/ic236-q4-ex3.png)

**输入：** n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
**输出：** 5
**解释：** 上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,3,3,4,4,5,4,3] ，最高建筑的高度为 5 。

提示：

  • 2 <= n <= 109
  • 0 <= restrictions.length <= min(n - 1, 105)
  • 2 <= idi <= n
  • idi 是 唯一的 。
  • 0 <= maxHeighti <= 109

方法一：限制的传递性

提示 1

由于每一栋建筑在数组 restrictions 中最多只会出现一次，为了叙述方便，我们将限制表示为 (i, h_i) 的形式，表示建筑 i 的高度不能超过 h_i。

虽然 (i, h_i) 是限制在建筑 i 之上的，但实际上，该限制也会对其余的建筑产生影响。

提示 1 解释

如果建筑 i 的高度不能超过 h_i，并且根据题目要求，相邻建筑的高度差不能超过 1，因此：

  • 建筑 i - 1 的高度不能超过 h_i+1；
  • 建筑 i + 1 的高度不能超过 h_i+1。

更一般地：

  • 建筑 j 的高度不能超过 h_i + |i-j|。

提示 2

根据提示 1，每一个限制 (i, h_i) 实际上是对所有 n 栋建筑的限制。如果我们通过某种方法将每一个限制「传递」开来，得到对第 i 栋建筑的真正的最低限制，记为 limit}_i，那么第 i 栋建筑的高度不能超过 limit}_i。

因此最优的建造方法，就是将第 i 栋建筑建造为高度 limit}_i。

提示 3

根据提示 2，我们可以确定每一栋建筑的高度，然而本题的数据范围为 n \leq 10^9，即使我们使用 O(n) 的方法得到所有的 limit}_i，也会超出时间（以及空间）限制。我们最多只能得到出现在限制数组中的那些建筑的 limit}_i。

那么对于剩余的建筑，你能找到一种方法快速确定它们的高度吗？

提示 3 解释

事实上，我们只需要关注的是「所有 n 栋建筑中的高度最大值」。

因此，如果有两栋建筑 i 和 j，满足 i < j 并且它们之间没有其它出现在限制数组里面的建筑，那么根据限制的传递性，i 到 j 之间建筑的高度应该形如一座「山脉」，即从建筑 i 开始，高度单调递增到达最大值，再单调递减到达建筑 j。

假设这个最大值为 best}(i, j)，那么需要满足：

\big( \textit{best}(i, j) - \textit{limit}_i \big) + \big( \textit{best}(i, j) - \textit{limit}_j \big) \leq j-i

解得

\textit{best}(i, j) = \lfloor (j - i) + \textit{limit}_i + \textit{limit}_j}{2} \rfloor

这样我们就可以得到「所有 n 栋建筑中的高度最大值」了。

思路与算法

首先我们需要求出所有的 limit}_i。

为了方便处理边界情况（即第 1 栋和第 n 栋建筑），我们可以在限制数组中增加 (1, 0) 和 (n, n-1) 这两个限制，随后将限制数组根据建筑编号为关键字升序排序。

随后我们就需要将每一个限制进行传递。一种简单的办法是对限制数组进行两次遍历，第一次遍历将限制「从左向右」传递，第二次遍历将限制「从右向左」传递：

  • 在「从左向右」传递的过程中，对于在限制数组中相邻的两项 (i, h_i) 以及 (j, h_j)，限制 (i, h_i) 传递到第 j 栋建筑会变为 (j, h_i + (j - i))，我们只需要将 h_j 更新为其和 h_i + (j - i) 中的较小值，就可以将第 j 栋建筑左侧的所有限制传递过来；

  • 在「从右向左」传递的过程中，对于在限制数组中相邻的两项 (i, h_i) 以及 (j, h_j)，限制 (j, h_j) 传递到第 i 栋建筑会变为 (i, h_j + (j - i))，我们只需要将 h_i 更新为其和 h_j + (j - i) 中的较小值，就可以将第 i 栋建筑右侧的所有限制传递过来。

在这之后，所有的 h_i 即为 limit}_i。我们只需要根据提示 3 求出最大值，即可得到最终的答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& restrictions) {
        auto&& r = restrictions;
        // 增加限制 (1, 0)
        r.push_back({1, 0});
        sort(r.begin(), r.end());

        // 增加限制 (n, n-1)
        if (r.back()[0] != n) {
            r.push_back({n, n - 1});
        }

        int m = r.size();
        
        // 从左向右传递限制
        for (int i = 1; i < m; ++i) {
            r[i][1] = min(r[i][1], r[i - 1][1] + (r[i][0] - r[i - 1][0]));
        }
        // 从右向左传递限制
        for (int i = m - 2; i >= 0; --i) {
            r[i][1] = min(r[i][1], r[i + 1][1] + (r[i + 1][0] - r[i][0]));
        }
            
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            // 计算 r[i][0] 和 r[i][1] 之间的建筑的最大高度
            int best = ((r[i + 1][0] - r[i][0]) + r[i][1] + r[i + 1][1]) / 2;
            ans = max(ans, best);
        }
        
        return ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int:
        r = restrictions
        # 增加限制 (1, 0)
        r.append([1, 0])
        r.sort()

        # 增加限制 (n, n-1)
        if r[-1][0] != n:
            r.append([n, n - 1])

        m = len(r)
        
        # 从左向右传递限制
        for i in range(1, m):
            r[i][1] = min(r[i][1], r[i - 1][1] + (r[i][0] - r[i - 1][0]))
        # 从右向左传递限制
        for i in range(m - 2, 0, -1):
            r[i][1] = min(r[i][1], r[i + 1][1] + (r[i + 1][0] - r[i][0]))
            
        ans = 0
        for i in range(m - 1):
            # 计算 r[i][0] 和 r[i][1] 之间的建筑的最大高度
            best = ((r[i + 1][0] - r[i][0]) + r[i][1] + r[i + 1][1]) // 2
            ans = max(ans, best)
        
        return ans

复杂度分析

  • 时间复杂度：O(m \log m)，其中 m 是数组 restrictions 的长度。我们需要将限制数组进行排序，时间复杂度为 O(m \log m)。后续对限制的两次传递以及计算高度的时间复杂度均为 O(m)，因此总时间复杂度为 O(m \log m)。

  • 空间复杂度：O(\log m)，即为排序需要使用的栈空间。

 Comments
On this page
1840-最高建筑高度