1878-矩阵中最大的三个菱形和

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

给你一个 m x n 的整数矩阵 grid 。

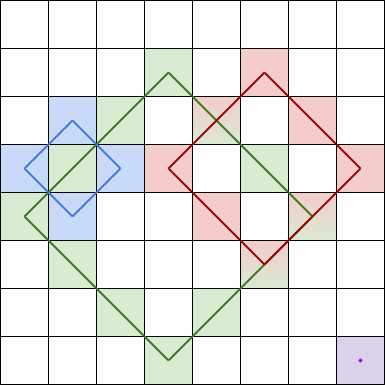
菱形和 指的是 grid 中一个正菱形 边界
上的元素之和。本题中的菱形必须为正方形旋转45度，且四个角都在一个格子当中。下图是四个可行的菱形，每个菱形和应该包含的格子都用了相应颜色标注在图中。

注意，菱形可以是一个面积为 0 的区域，如上图中右下角的紫色菱形所示。

请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和 。如果不同的和少于三个，则将它们全部返回。

示例 1：

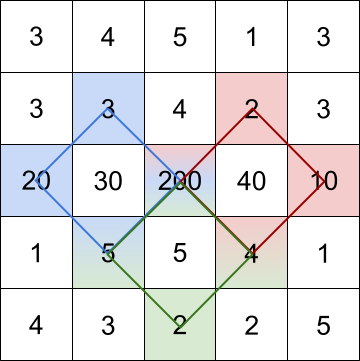
**输入：** grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
**输出：** [228,216,211]
**解释：** 最大的三个菱形和如上图所示。
- 蓝色：20 + 3 + 200 + 5 = 228
- 红色：200 + 2 + 10 + 4 = 216
- 绿色：5 + 200 + 4 + 2 = 211

示例 2：

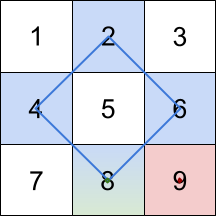
**输入：** grid = [[1,2,3],[4,5,6],[7,8,9]]
**输出：** [20,9,8]
**解释：** 最大的三个菱形和如上图所示。
- 蓝色：4 + 2 + 6 + 8 = 20
- 红色：9 （右下角红色的面积为 0 的菱形）
- 绿色：8 （下方中央面积为 0 的菱形）

示例 3：

**输入：** grid = [[7,7,7]]
**输出：** [7]
**解释：** 所有三个可能的菱形和都相同，所以返回 [7] 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • 1 <= grid[i][j] <= 105

方法一：枚举所有的菱形

提示 1

一个菱形的自由度是多少（即如果我们至少需要多少个变量，才能唯一表示一个菱形）？

提示 1 解释

一个菱形的自由度是 3，例如：

2 个变量表示菱形上顶点的坐标，1 个变量表示菱形在水平或者竖直方向上的宽度。

提示 2

fig1

提示 3

要想快速计算提示 2 中的每一部分，我们可以使用前缀和。

  • 记 sum}_1[x][y] 表示从位置 (x-1, y-1) 开始往左上方走，走到边界为止的所有格子的元素和。

  • 记 sum}_2[x][y] 表示从位置 (x-1, y-1) 开始往右上方走，走到边界为止的所有格子的元素和。

思路与算法

我们首先可以使用二重循环预处理出所有的 sum}_1[i][j] 以及 sum}_2[i][j]。具体地，有递推式：

\textit{sum}_1[i][j] = \textit{sum}_1[i-1][j-1] + \textit{grid}[i-1][j-1]

以及：

\textit{sum}_2[i][j] = \textit{sum}_2[i-1][j+1] + \textit{grid}[i-1][j-1]

其中 i 和 j 的范围分别为 [1, m] 以及 [1, n]。

接下来，我们使用三重循环分别枚举菱形上顶点的位置以及其在水平方向上的宽度，就可以计算出菱形四个顶点的位置，上下左右顶点的位置依次记为 (u_x, u_y)，(d_x, d_y)，(l_x, l_y) 以及 (r_x, r_y)。这样一来，我们就可以使用前缀和在 O(1) 的时间计算该菱形的菱形和，即提示 2 中的五个部分的和分别为：

\begin{cases}
\textit{sum}_2[l_x + 1][l_y + 1] - \textit{sum}_2[u_x][u_y + 2] \
\textit{sum}_1[r_x + 1][r_y + 1] - \textit{sum}_1[u_x][u_y] \
\textit{sum}_1[d_x + 1][d_y + 1] - \textit{sum}_1[l_x][l_y] \
\textit{sum}_2[d_x + 1][d_y + 1] - \textit{sum}_2[r_x][r_y + 2] \
\textit{grid}[u_x][u_y] + \textit{grid}[d_x][d_y] + \textit{grid}[l_x][l_y] + \textit{grid}[r_x][r_y]
\end{cases}

除此之外，我们可以设计一个简单的数据结构，它使得我们在得到了菱形和后，可以实时维护最大的 3 个互不相同的菱形和，具体的实现可以参考下面的代码。

细节

需要注意单独的一个格子也是菱形。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
struct Answer {
    array<int, 3> ans{};
    
    void put(int x) {
        if (x > ans[0]) {
            tie(ans[0], ans[1], ans[2]) = tuple{x, ans[0], ans[1]};
        }
        else if (x != ans[0] && x > ans[1]) {
            tie(ans[1], ans[2]) = tuple{x, ans[1]};
        }
        else if (x != ans[0] && x != ans[1] && x > ans[2]) {
            ans[2] = x;
        }
    }
    
    vector<int> get() const {
        vector<int> ret;
        for (int num: ans) {
            if (num) {
                ret.push_back(num);
            }
        }
        return ret;
    }
};

class Solution {
public:
    vector<int> getBiggestThree(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> sum1(m + 1, vector<int>(n + 2));
        vector<vector<int>> sum2(m + 1, vector<int>(n + 2));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                sum1[i][j] = sum1[i - 1][j - 1] + grid[i - 1][j - 1];
                sum2[i][j] = sum2[i - 1][j + 1] + grid[i - 1][j - 1];
            }
        }
        Answer ans;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                // 单独的一个格子也是菱形
                ans.put(grid[i][j]);
                for (int k = i + 2; k < m; k += 2) {
                    int ux = i, uy = j;
                    int dx = k, dy = j;
                    int lx = (i + k) / 2, ly = j - (k - i) / 2;
                    int rx = (i + k) / 2, ry = j + (k - i) / 2;
                    if (ly < 0 || ry >= n) {
                        break;
                    }
                    ans.put(
                        (sum2[lx + 1][ly + 1] - sum2[ux][uy + 2]) +
                        (sum1[rx + 1][ry + 1] - sum1[ux][uy]) +
                        (sum1[dx + 1][dy + 1] - sum1[lx][ly]) +
                        (sum2[dx + 1][dy + 1] - sum2[rx][ry + 2]) -
                        (grid[ux][uy] + grid[dx][dy] + grid[lx][ly] + grid[rx][ry])
                    );
                }
            }
        }
        return ans.get();
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Answer:
    def __init__(self):
        self.ans = [0, 0, 0]
    
    def put(self, x: int):
        _ans = self.ans

        if x > _ans[0]:
            _ans[0], _ans[1], _ans[2] = x, _ans[0], _ans[1]
        elif x != _ans[0] and x > _ans[1]:
            _ans[1], _ans[2] = x, _ans[1]
        elif x != _ans[0] and x != _ans[1] and x > _ans[2]:
            _ans[2] = x
    
    def get(self) -> List[int]:
        _ans = self.ans

        return [num for num in _ans if num != 0]


class Solution:
    def getBiggestThree(self, grid: List[List[int]]) -> List[int]:
        m, n = len(grid), len(grid[0])
        sum1 = [[0] * (n + 2) for _ in range(m + 1)]
        sum2 = [[0] * (n + 2) for _ in range(m + 1)]

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                sum1[i][j] = sum1[i - 1][j - 1] + grid[i - 1][j - 1]
                sum2[i][j] = sum2[i - 1][j + 1] + grid[i - 1][j - 1]
        
        ans = Answer()
        for i in range(m):
            for j in range(n):
                # 单独的一个格子也是菱形
                ans.put(grid[i][j])
                for k in range(i + 2, m, 2):
                    ux, uy = i, j
                    dx, dy = k, j
                    lx, ly = (i + k) // 2, j - (k - i) // 2
                    rx, ry = (i + k) // 2, j + (k - i) // 2
                    
                    if ly < 0 or ry >= n:
                        break
                    
                    ans.put(
                        (sum2[lx + 1][ly + 1] - sum2[ux][uy + 2]) +
                        (sum1[rx + 1][ry + 1] - sum1[ux][uy]) +
                        (sum1[dx + 1][dy + 1] - sum1[lx][ly]) +
                        (sum2[dx + 1][dy + 1] - sum2[rx][ry + 2]) -
                        (grid[ux][uy] + grid[dx][dy] + grid[lx][ly] + grid[rx][ry])
                    )
        
        return ans.get()

复杂度分析

  • 时间复杂度：O(mn \min(m, n))。预处理前缀和的时间复杂度为 O(mn)，枚举菱形并计算菱形和的时间复杂度为 O(mn \min(m, n))，因此总时间复杂度为 O(mn \min(m, n))。

  • 空间复杂度：O(mn)，记为前缀和数组需要使用的空间。

 Comments
On this page
1878-矩阵中最大的三个菱形和