1886-判断矩阵经轮转后是否一致

给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素
若干次 ，如果能够使 mat 与 target 一致，返回 true ；否则，返回 __false 。

示例 1：

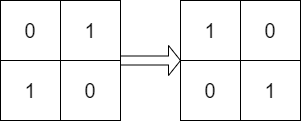
**输入：** mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
**输出：** true
**解释：** 顺时针轮转 90 度一次可以使 mat 和 target 一致。

示例 2：

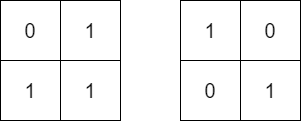
**输入：** mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
**输出：** false
**解释：** 无法通过轮转矩阵中的元素使 equal 与 target 一致。

示例 3：

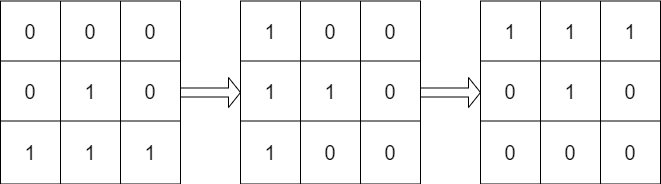
**输入：** mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
**输出：** true
**解释：** 顺时针轮转 90 度两次可以使 mat 和 target 一致。

提示：

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] 和 target[i][j] 不是 0 就是 1

方法一：模拟轮转操作

提示 1

将一个矩阵 90 度顺时针旋转 4 次，旋转后的矩阵与本身一致。

思路与算法

根据 提示 1，我们可以模拟 4 次将 mat 90 度顺时针旋转的操作，并在每次旋转操作后与 target 比较。

对于旋转操作，可以建立额外数组实现，也可以原地旋转。不同方法的具体细节与相关推导读者可以参考「48. 旋转图像」的题解 。

本文中，我们采用原地旋转的方式（即上文题解链接中的 方法二）实现旋转操作。

代码

[sol1-C++]

class Solution {
public:
    int temp;
    bool flag;

    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        int n = mat.size();
        // 最多旋转 4 次
        for (int k = 0; k < 4; ++k) {
            // 旋转操作
            for (int i = 0; i < n / 2; ++i) {
                for (int j = 0; j < (n + 1) / 2; ++j) {
                    temp = mat[i][j];
                    mat[i][j] = mat[n-1-j][i];
                    mat[n-1-j][i] = mat[n-1-i][n-1-j];
                    mat[n-1-i][n-1-j] = mat[j][n-1-i];
                    mat[j][n-1-i] = temp;
                }
            }
            
            if (mat == target) {
                return true;
            }
        }
        return false;    
    }
};

[sol1-Python3]

class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        n = len(mat)
        # 最多旋转 4 次
        for k in range(4):
            # 旋转操作
            for i in range(n // 2):
                for j in range((n + 1) // 2):
                    mat[i][j], mat[n-1-j][i], mat[n-1-i][n-1-j], mat[j][n-1-i] \
                        = mat[n-1-j][i], mat[n-1-i][n-1-j], mat[j][n-1-i], mat[i][j]
            
            if mat == target:
                return True
        return False

复杂度分析

• 时间复杂度：O(n^2)，其中 n 为 mat 的边长。我们最多进行 4 次旋转与比较操作，每次旋转操作的时间复杂度为 O(n^2)，每次比较操作的时间复杂度为 O(n^2)。

• 空间复杂度：O(1)。