1901-寻找峰值 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 11:10:04 2023-09-13 11:10:04 Updated    

一个 2D 网格中的 峰值 **** 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值
mat[i][j] 并 返回其位置[i,j] 。

你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

示例 1:

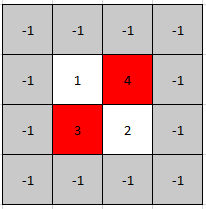
**输入:** mat = [[1,4],[3,2]]
**输出:** [0,1]
**解释:**  3 和 4 都是峰值，所以[1,0]和[0,1]都是可接受的答案。

示例 2:

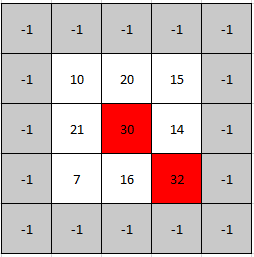
**输入:** mat = [[10,20,15],[21,30,14],[7,16,32]]
**输出:** [1,1]
**解释:**  30 和 32 都是峰值，所以[1,1]和[2,2]都是可接受的答案。

提示：

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 500
  • 1 <= mat[i][j] <= 105
  • 任意两个相邻元素均不相等.

解题思路

本题解中会解释为什么 O(nlogm/mlogn) 可以，以及为什么 O(log(m+n)) 不行。

我们首先要想，这个题和找 max(max(mat)) 的区别是什么？也就是，可以将时间复杂度从 O(mn) 降至 O(nlogm/mlogn) 的关键点在于什么？
是的，关键点就在于极值点是可以提前剪枝的。只要我们找到了一个极值点，就可以提前跳出，而不需要查看其他的部分。

这样，我们就可以使用二分法进行切片。我们以一维数组举例：

QQ截图20220113164859.png

我们首先找到中间的9。发现其右侧数字比它大，那么我们就可以知道：[10,1,4]中一定存在极大值。我们只需要看右侧子数组即可。继续二分，关注1，我们发现左右数字都比它大，随便选取一个。比如我们选取[4]这个子数组，发现长度为1，那么4就是一个极大值。

理解了一维数组，我们再看二维数组：

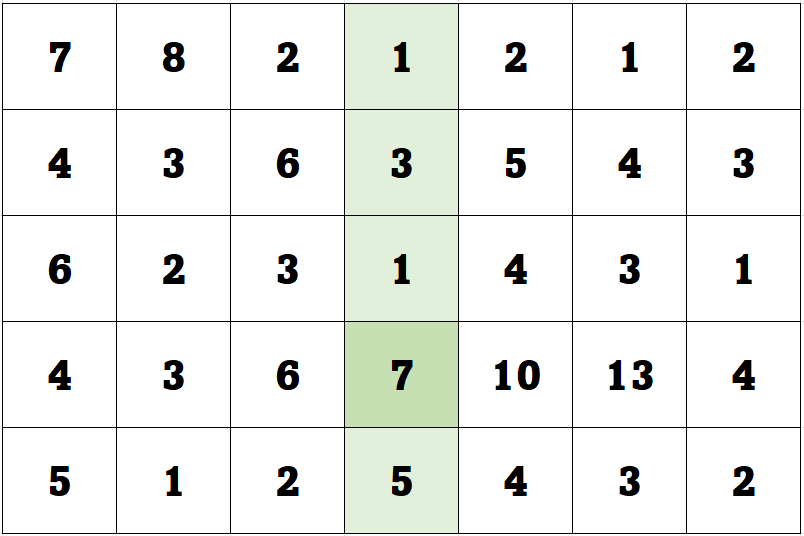
QQ截图20220113165416.png

我们回想一维数组切片的过程。为什么我们能对mid左右的元素进行切片？其逻辑在于，当我们发现mid右侧元素大于mid时，其右侧肯定存在大于mid的元素。这听上去像是一句废话，但是当我们面临二维数组时，就是一个关键的判断点。我们仍然仿照一维数组，选取中间的一列元素，即[1,3,1,7,5]^T，我们现在拿着这个数组，希望仿照一维数组的判断逻辑进行切片。我们还想找到能证明其右侧肯定存在大于mid的元素的标志，那是什么呢？是的，很简单，只要我们找到[1,3,1,7,5]^T中的最大值7，发现其右侧元素大于7，那么其右侧肯定存在大于mid的元素。

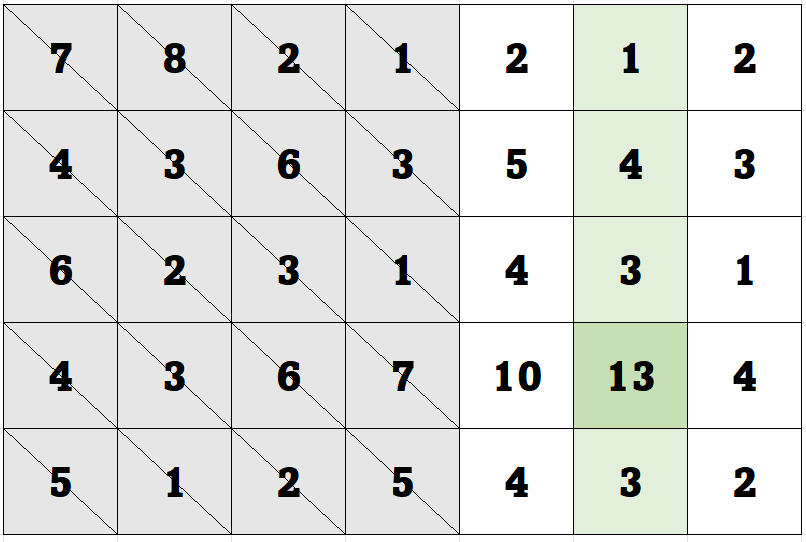
QQ截图20220113171444.png

我们将mid列左侧的舍弃，观察右侧的切片，重复这个过程。我们发现这次Mid列中最大的元素13比左右都大，那么我们就找到了一个极值。
因此，我们找到了一种应用列二分进行查找的办法。这个方法二分的时间复杂度为 O(logn)，查找最大值为 O(m)，合起来为 O(nlogm/mlogn)。

有些朋友会想，能不能把这个时间复杂度进一步压缩呢？我们能不能不找一列的最大值，而是找极值呢？这样，我们在搜索单列的极值时也可以使用二分法，这样时间复杂度就下降到 O(logm*logn) = O(log(m+n)) 了。
很可惜，理想很丰满，现实很骨感。如果我们只找极大值，很可能会遇到连续的鞍点，从而陷入局部循环。
我们依然用刚才的二维数组。在第一次搜索时，我们搜索到了一个局部极大值3，此时我们其实已经看到3就是一个鞍点。我们规定如果两侧数据都比中间大，我们选取右边的切片（这个对结果没有任何影响，如果规定选取左边，那把例子中的数组翻转就好）。

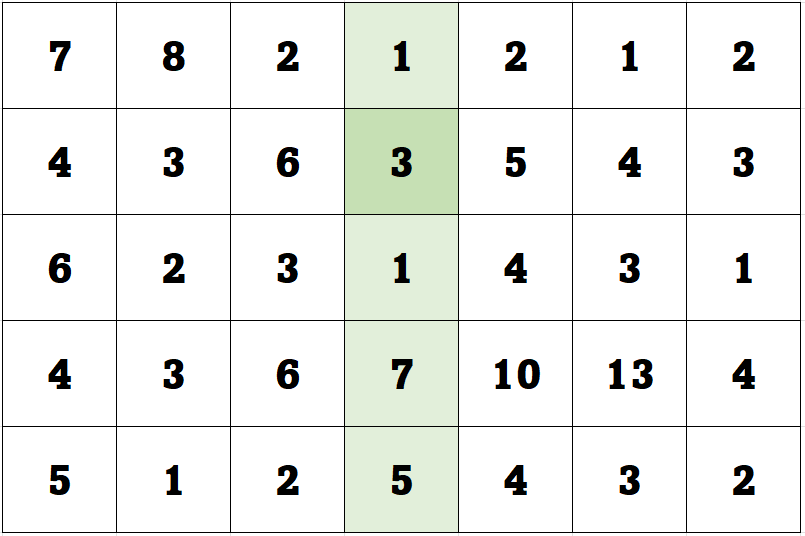
QQ截图20220113172226.png

再次继续搜索，我们找到一个极值点4。左边元素更大，我们选取其左边的切片。

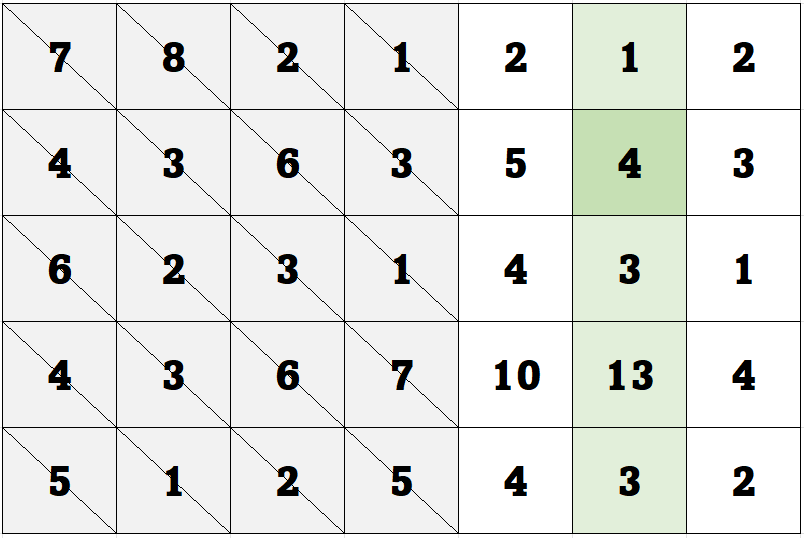
QQ截图20220113172327.png

我们只剩一列了，以之前的算法而言，找到这列的极大值，其就应该是二维数组的极大值。我们找到了极大值10（我例子举的不好，所以最后一张图把中间的4改成6，但其实无伤大雅，因为我们本来也有可能选到10作为极大值，只是改了之后就一定会选10）。

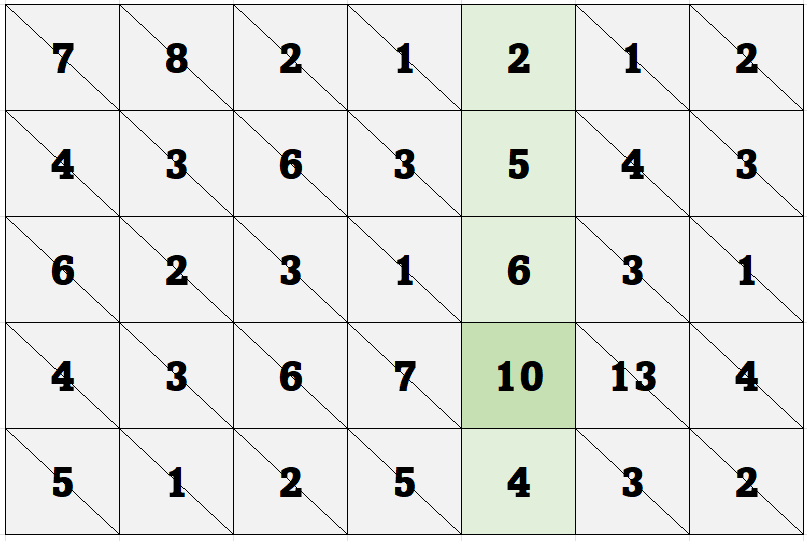
QQ截图20220113172627.png

这时我们发现，10根本不是极大值，原本右侧的13应该是极大值，但是13在他的列中却没有竞争过另一个极大值4，导致被略过了。接下来，算法将在这两列中无限循环。

因此，我们可以发现这样是不合理的，在单列中必须选取最大值而不是极大值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
    def findPeakGrid(self, mat: List[List[int]]) -> List[int]:

        m, n = len(mat), len(mat[0])

        # 找到单列中最大值和其索引
        def getColMax(i: int) -> (int, int):
            value, index = mat[0][i], 0
            for row in range(1, m):
                if mat[row][i] > value:
                    value, index = mat[row][i], row
            return value, index

        # 二分法切片
        left, right = 0, n - 1
        while left < right:
            mid = left + int((right-left)/2)
            max_val, max_idx = getColMax(mid)
            if mid == 0: # left = 0, right = 1
                if max_val > mat[max_idx][1]:
                    return [max_idx, 0]
                else:
                    left = 1
            else:
                if mat[max_idx][mid-1] < max_val and mat[max_idx][mid+1] < max_val:
                    return [max_idx, mid]
                elif mat[max_idx][mid-1] < max_val < mat[max_idx][mid+1]:
                    left = mid + 1
                else:
                    right = mid - 1
        
        # 对于最后剩下的一列，其最大值一定是极大值
        _, idx = getColMax(left)
        return [idx, left]
 Comments
On this page
1901-寻找峰值 II
  1. 解题思路
  2. 代码