给你一个大小为 m x n 的整数矩阵 grid ,其中 m 和 n 都是 偶数 ;另给你一个整数 k 。
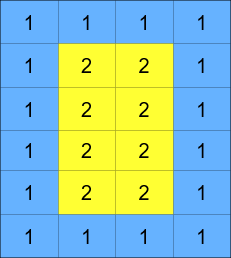
矩阵由若干层组成,如下图所示,每种颜色代表一层:

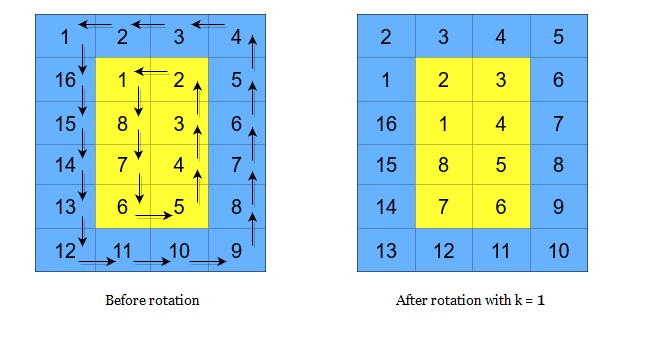
矩阵的循环轮转是通过分别循环轮转矩阵中的每一层完成的。在对某一层进行一次循环旋转操作时,层中的每一个元素将会取代其 逆时针
方向的相邻元素。轮转示例如下:

返回执行 k 次循环轮转操作后的矩阵。
示例 1:

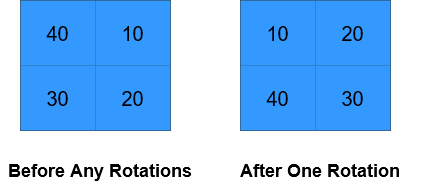
**输入:** grid = [[40,10],[30,20]], k = 1
**输出:** [[10,20],[40,30]]
**解释:** 上图展示了矩阵在执行循环轮转操作时每一步的状态。
示例 2:



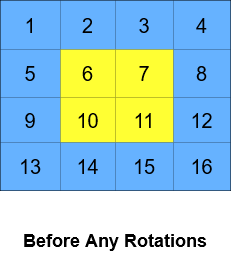
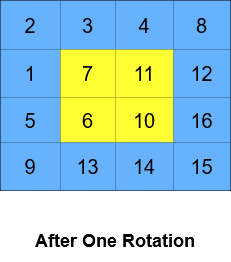
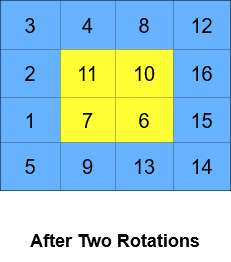
**输入:** grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
**输出:** [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
**解释:** 上图展示了矩阵在执行循环轮转操作时每一步的状态。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 50m 和 n 都是 偶数1 <= grid[i][j] <= 50001 <= k <= 109
方法一:枚举每一层
思路与算法
对于一个 m \times n 的矩阵 grid,它的层数为 \min(m / 2, n / 2)。我们可以从外向内枚举矩阵的每一层模拟循环轮转操作。
为了方便模拟,我们从左上角起按照逆时针方向遍历每一层的元素。在本文中,我们将遍历过程分为四个部分,每个部分按顺序遍历每条边除了最后一个元素以外的所有元素。
我们将这些元素的行坐标、列坐标与数值保存在对应的数组 r, c, \textit{val 中,并计算元素总数,即数组的长度 total。此时,如果对该层元素进行 total 次循环轮转操作,那么该层元素不会改变。因此,实际的循环轮转操作数量即为 kk} = k % \textit{total。
那么,这一层中遍历到的第 i 个位置在轮转操作后存放的值对应 val 数组中下标为 (i - \textit{kk} + \textit{total}) % \textit{total 的值。此处在取模时加上 total 是为了避免出现负数。
我们遍历行列坐标数组,并在 grid 中更新每个坐标对应的轮转操作后的取值。当枚举并更新完所有层后,grid 即为轮转操作后的矩阵。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public:
vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
int m = grid.size();
int n = grid[0].size();
int nlayer = min(m / 2, n / 2);
for (int layer = 0; layer < nlayer; ++layer){
vector<int> r, c, val;
for (int i = layer; i < m - layer - 1; ++i){
r.push_back(i);
c.push_back(layer);
val.push_back(grid[i][layer]);
}
for (int j = layer; j < n - layer - 1; ++j){
r.push_back(m - layer - 1);
c.push_back(j);
val.push_back(grid[m-layer-1][j]);
}
for (int i = m - layer - 1; i > layer; --i){
r.push_back(i);
c.push_back(n - layer - 1);
val.push_back(grid[i][n-layer-1]);
}
for (int j = n - layer - 1; j > layer; --j){
r.push_back(layer);
c.push_back(j);
val.push_back(grid[layer][j]);
}
int total = val.size();
int kk = k % total;
for (int i = 0; i < total; ++i){
int idx = (i + total - kk) % total;
grid[r[i]][c[i]] = val[idx];
}
}
return grid;
}
};
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution:
def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
m, n = len(grid), len(grid[0])
nlayer = min(m // 2, n // 2)
for layer in range(nlayer):
r = []
c = []
val = []
for i in range(layer, m - layer - 1):
r.append(i)
c.append(layer)
val.append(grid[i][layer])
for j in range(layer, n - layer - 1):
r.append(m - layer - 1)
c.append(j)
val.append(grid[m-layer-1][j])
for i in range(m - layer - 1, layer, -1):
r.append(i)
c.append(n - layer - 1)
val.append(grid[i][n-layer-1])
for j in range(n - layer - 1, layer, -1):
r.append(layer)
c.append(j)
val.append(grid[layer][j])
total = len(val)
kk = k % total
for i in range(total):
idx = (i + total - kk) % total
grid[r[i]][c[i]] = val[idx]
return grid
|
复杂度分析