1926-迷宫中离入口最近的出口
给你一个 m x n 的迷宫矩阵 maze ( 下标从 0 开始 ),矩阵中有空格子(用 '.' 表示)和墙(用 '+'
表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol]
表示你一开始所在格子的行和列。
每一步操作,你可以往 上 , 下 , 左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离entrance 最近 的出口。 出口 的含义是 maze 边界 上的 空格子 。entrance 格子
不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。
示例 1:
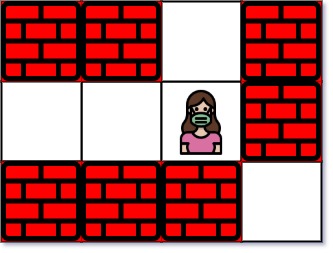
**输入:** maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
**输出:** 1
**解释:** 总共有 3 个出口,分别位于 (1,0),(0,2) 和 (2,3) 。
一开始,你在入口格子 (1,2) 处。
- 你可以往左移动 2 步到达 (1,0) 。
- 你可以往上移动 1 步到达 (0,2) 。
从入口处没法到达 (2,3) 。
所以,最近的出口是 (0,2) ,距离为 1 步。
示例 2:

**输入:** maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
**输出:** 2
**解释:** 迷宫中只有 1 个出口,在 (1,2) 处。
(1,0) 不算出口,因为它是入口格子。
初始时,你在入口与格子 (1,0) 处。
- 你可以往右移动 2 步到达 (1,2) 处。
所以,最近的出口为 (1,2) ,距离为 2 步。
示例 3:

**输入:** maze = [[".","+"]], entrance = [0,0]
**输出:** -1
**解释:** 这个迷宫中没有出口。
提示:
maze.length == mmaze[i].length == n1 <= m, n <= 100maze[i][j]要么是'.',要么是'+'。entrance.length == 20 <= entrancerow < m0 <= entrancecol < nentrance一定是空格子。
方法一:广度优先搜索
思路与算法
我们可以使用广度优先搜索来寻找迷宫中距离入口最近的出口。
在广度优先搜索的过程中,我们在队列中保存 (c_x, c_y, d) 三元组,其中 (c_x, c_y) 为当前的行列坐标, d 为当前坐标相对入口的距离。
当我们遍历至 (c_x, c_y) 时,我们枚举它上下左右的相邻坐标 (n_x, n_y)。此时可能有三种情况:
(n_x, n_y) 不合法或对应的坐标为墙,此时无需进行任何操作;
(n_x, n_y) 为迷宫的出口(在迷宫边界且不为墙),此时应返回 d + 1,即该出口相对入口的距离作为答案。
(n_x, n_y) 为空格子且不为出口,此时应将新坐标对应的三元组 (n_x, n_y, d + 1) 加入队列。
最终,如果不存在到达出口的路径,我们返回 -1 作为答案。
为了避免重复遍历,我们可以将所有遍历过的坐标对应迷宫矩阵的值改为墙所对应的字符 `+’。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(mn),其中 m, n 分别为迷宫矩阵的行数与列数。即为广度优先搜索的时间复杂度。
空间复杂度:O(mn),即为广度优先搜索中队列需要使用的空间。