1928-规定时间内到达终点的最小花费

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组
edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为
timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中
passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的
费用 为你经过的所有城市 通行费之和 （ 包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime
分钟以内完成旅行，请你返回 -1 。

示例 1：

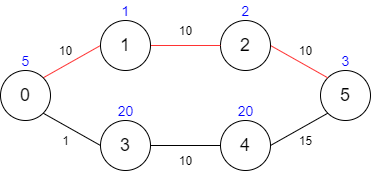
**输入：** maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
**输出：** 11
**解释：** 最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。

示例 2：

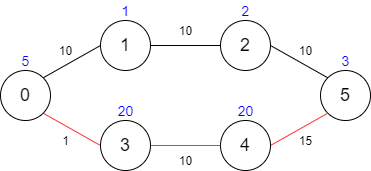
![](https://assets.leetcode.com/uploads/2021/06/04/copy-of-
leetgraph1-1.png)

**输入：** maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
**输出：** 48
**解释：** 最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。

示例 3：

**输入：** maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
**输出：** -1
**解释：** 无法在 25 分钟以内从城市 0 到达城市 5 。

提示：

  • 1 <= maxTime <= 1000
  • n == passingFees.length
  • 2 <= n <= 1000
  • n - 1 <= edges.length <= 1000
  • 0 <= xi, yi <= n - 1
  • 1 <= timei <= 1000
  • 1 <= passingFees[j] <= 1000
  • 图中两个节点之间可能有多条路径。
  • 图中不含有自环。

方法一：动态规划

思路与算法

我们用 f[t][i] 表示使用恰好 t 分钟到达城市 i 需要的最少通行费总和。

在状态转移时，我们考虑最后一次通行是从城市 j 到达城市 i 的，那么有状态转移方程：

f[t][i] = \min_{(j, i) \in E} \big{ f[t-\textit{cost}(j, i)][j] + \textit{passingFees}[i] \big}

其中 (j, i) \in E 表示城市 j 与 i 存在一条道路，cost}(j, i) 表示这条道路的耗费时间。

最终的答案即为 f[1][n-1], f[2][n-1], \cdots, f[\textit{maxTime}][n-1] 中的最小值。

细节

初始状态为 f[0][0] = \textit{passingFees}[0]，即我们一开始位于 0 号城市，需要交 passingFees}[0] 的通行费。

由于我们的状态转移方程中的目标的最小值，因此对于其它的状态，我们可以在一开始赋予它们一个极大值 \infty。如果最终的答案为 \infty，说明无法在 maxTime 及以内完成旅行，返回 -1。

此外，本题中的道路是以数组 edges 的形式给定的，在动态规划的过程中，如果我们使用两重循环枚举 t 和 i，就不能利用 edges，而需要使用额外的数据结构存储以 i 为端点的所有道路。一种合理的解决方法是，我们使用一重循环枚举 t，另一重循环枚举 edges 中的每一条边 (i, j, \textit{cost})，通过这条边更新 f[t][i] 以及 f[t][j] 的值。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
private:
    // 极大值
    static constexpr int INFTY = INT_MAX / 2;

public:
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
        int n = passingFees.size();
        vector<vector<int>> f(maxTime + 1, vector<int>(n, INFTY));
        f[0][0] = passingFees[0];
        for (int t = 1; t <= maxTime; ++t) {
            for (const auto& edge: edges) {
                int i = edge[0], j = edge[1], cost = edge[2];
                if (cost <= t) {
                    f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i]);
                    f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j]);
                }
            }
        }

        int ans = INFTY;
        for (int t = 1; t <= maxTime; ++t) {
            ans = min(ans, f[t][n - 1]);
        }
        return ans == INFTY ? -1 : ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
        n = len(passingFees)
        f = [[float("inf")] * n for _ in range(maxTime + 1)]
        f[0][0] = passingFees[0]
        for t in range(1, maxTime + 1):
            for i, j, cost in edges:
                if cost <= t:
                    f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i])
                    f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j])

        ans = min(f[t][n - 1] for t in range(1, maxTime + 1))
        return -1 if ans == float("inf") else ans

复杂度分析

  • 时间复杂度：O((n+m) \cdot \textit{maxTimes})，其中 m 是数组 edges 的长度。

    • 我们需要 O(n \cdot \textit{maxTimes}) 的时间初始化数组 f；

    • 动态规划需要的时间为 O(m \cdot \textit{maxTimes})。

  • 空间复杂度：O(n \cdot \textit{maxTimes})。

 Comments
On this page
1928-规定时间内到达终点的最小花费