1931-用三种不同颜色为网格涂色
给你两个整数 m 和 n 。构造一个 m x n 的网格,其中每个单元格最开始是白色。请你用 红、绿、蓝
三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足: 不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大, 返回 对109 + 7
取余 的结果。
示例 1:

**输入:** m = 1, n = 1
**输出:** 3
**解释:** 如上图所示,存在三种可能的涂色方案。
示例 2:
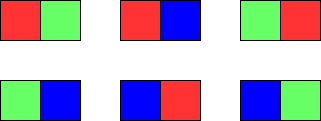
**输入:** m = 1, n = 2
**输出:** 6
**解释:** 如上图所示,存在六种可能的涂色方案。
示例 3:
**输入:** m = 5, n = 5
**输出:** 580986
提示:
1 <= m <= 51 <= n <= 1000
方法一:状态压缩动态规划
提示 1
要使得任意两个相邻的格子的颜色均不相同,我们需要保证:
同一行内任意两个相邻格子的颜色互不相同;
相邻的两行之间,同一列上的两个格子的颜色互不相同。
因此,我们可以考虑:
首先通过枚举的方法,找出所有对一行进行涂色的方案数;
然后通过动态规划的方法,计算出对整个 m \times n 的方格进行涂色的方案数。
在本题中,m 和 n 的最大值分别是 5 和 1000,我们需要将较小的 m 看成行的长度,较大的 n 看成列的长度,这样才可以对一行进行枚举。
思路与算法
我们首先枚举对一行进行涂色的方案数。
对于我们可以选择红绿蓝三种颜色,我们可以将它们看成 0, 1, 2。这样一来,一种涂色方案就对应着一个长度为 m 的三进制数,其十进制的范围为 [0, 3^m)。
因此,我们可以枚举 [0, 3^m) 范围内的所有整数,将其转换为长度为 m 的三进制串,再判断其是否满足任意相邻的两个数位均不相同即可。
随后我们就可以使用动态规划来计算方案数了。我们用 f[i][\textit{mask}] 表示我们已经对 0, 1, \cdots, i 行进行了涂色,并且第 i 行的涂色方案对应的三进制表示为 mask 的前提下的总方案数。在进行状态转移时,我们可以考虑第 i-1 行的涂色方案 mask}’:
f[i][\textit{mask}] = \sum_{\textit{mask} 与 \textit{mask}’ 同一数位上的数字均不相同} f[i-1][\textit{mask}’]
只要 mask}’ 与 mask 同一数位上的数字均不相同,就说明这两行可以相邻,我们就可以进行状态转移。
最终的答案即为所有满足 mask} \in [0, 3^m) 的 f[n-1][\textit{mask}] 之和。
细节
上述动态规划中的边界条件在于第 0 行的涂色。当 i=0 时,f[i-1][..] 不是合法状态,无法进行转移,我们需要对它们进行特判:即如果 mask 任意相邻的两个数位均不相同,那么 f[0][\textit{mask}] = 1,否则 f[0][\textit{mask}] = 0。
在其余情况下的状态转移时,对于给定的 mask,我们总是要找出所有满足要求的 mask}’,因此我们不妨也把它们预处理出来,具体可以参考下方给出的代码。
最后需要注意的是,在状态转移方程中,f[i][..] 只会从 f[i-1][..] 转移而来,因此我们可以使用两个长度为 3^m 的一维数组,交替地进行状态转移。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(3^{2m} \cdot n)。
预处理 mask 的时间复杂度为 O(m \cdot 3^m);
预处理 (\textit{mask}, \textit{mask}’) 二元组的时间复杂度为 O(3^{2m});
动态规划的时间复杂度为 O(3^{2m} \cdot n),其在渐近意义下大于前两者。
空间复杂度:O(3^{2m})。
存储 mask 的哈希映射需要的空间为 O(m \cdot 3^m);
存储 (\textit{mask}, \textit{mask}’) 二元组需要的空间为 O(3^{2m}),在渐进意义下大于其余两者;
动态规划存储状态需要的空间为 O(3^m)。
不过需要注意的是,在实际的情况下,当 m=5 时,满足要求的 mask 仅有 48 个,远小于 3^m=243;满足要求的 (\textit{mask}, \textit{mask}’) 二元组仅有 486 对,远小于 3^{2m}=59049。因此该算法的实际运行时间会较快。