1937-扣分后的最大得分

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

给你一个 m x n 的整数矩阵 points （下标从 0 开始）。一开始你的得分为 0 ，你想最大化从矩阵中得到的分数。

你的得分方式为： 每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。

然而，相邻行之间被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为
(r, c1) 和 (r + 1, c2) 的格子，你的总得分 减少 abs(c1 - c2) 。

请你返回你能得到的 最大 得分。

abs(x) 定义为：

  • 如果 x >= 0 ，那么值为 x 。
  • 如果 x < 0 ，那么值为 -x 。

示例 1：

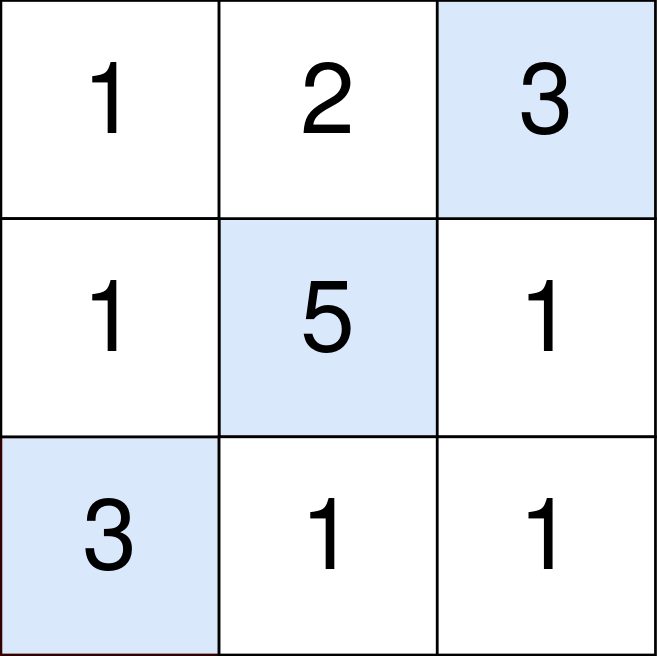
![](https://assets.leetcode.com/uploads/2021/07/12/screenshot-2021-07-12-at-13-40-26-diagram-
drawio-diagrams-net.png)

**输入：** points = [[1,2,3],[1,5,1],[3,1,1]]
**输出：** 9
**解释：**
蓝色格子是最优方案选中的格子，坐标分别为 (0, 2)，(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。

示例 2：

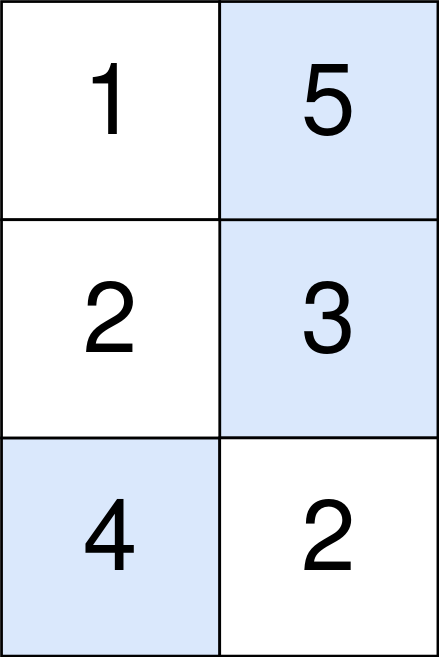
![](https://assets.leetcode.com/uploads/2021/07/12/screenshot-2021-07-12-at-13-42-14-diagram-
drawio-diagrams-net.png)

**输入：** points = [[1,5],[2,3],[4,2]]
**输出：** 11
**解释：**
蓝色格子是最优方案选中的格子，坐标分别为 (0, 1)，(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。

提示：

  • m == points.length
  • n == points[r].length
  • 1 <= m, n <= 105
  • 1 <= m * n <= 105
  • 0 <= points[r][c] <= 105

方法一：动态规划

思路与算法

记 f[i][j] 表示当我们在第 0, 1, \cdots, i 行均选择了一个格子，并且第 i 行选择的格子为 (i, j) 时的最大分数。在进行状态转移时，我们可以枚举第 i-1 行选择的格子 j’，这样就可以得到状态转移方程：

f[i][j] = \max \big{ f[i-1][j’] - |j - j’| \big} + \textit{points}[i][j]

最终的答案即为 f[m-1][0..n-1] 中的最大值。

然而上述动态规划的时间复杂度为 O(mn^2)，因为总计有 mn 个状态，而对于每个状态我们需要 O(n) 的时间枚举 j’ 进行转移，这样很容易超出时间限制，因此我们需要进行优化。

优化

优化的重点在于状态转移方程中的 |j-j’| 这一项。

当 j’ \leq j 时，|j - j’| = j - j’，状态转移方程变为：

\begin{aligned}
f[i][j] &= \max \big{ f[i-1][j’] - j + j’ \big} + \textit{points}[i][j] \
&= \max \big{ f[i-1][j’] + j’ \big} + \textit{points}[i][j] - j
\end{aligned}

这样一来，我们只需要在满足 j’ \leq j 的前提下，找出最大的 f[i-1][j’] + j’ 进行转移即可。我们只需要在 [0, n-1] 的范围内正序地遍历一遍 j，即可在 O(n) 的时间完成这一部分的状态转移。

同理，当 j’ > j 时，|j - j’| = j’ - j，状态转移方程变为：

\begin{aligned}
f[i][j] &= \max \big{ f[i-1][j’] - j’ + j \big} + \textit{points}[i][j] \
&= \max \big{ f[i-1][j’] - j’ \big} + \textit{points}[i][j] + j
\end{aligned}

这样一来，我们只需要在满足 j’ > j 的前提下，找出最大的 f[i-1][j’] - j’ 进行转移即可。我们只需要在 [0, n-1] 的范围内倒序地遍历一遍 j，即可在 O(n) 的时间完成这一部分的状态转移。

在进行了两次 O(n) 的遍历后，我们就得到了所有 f[i][0..n-1] 的值，动态规划的总时间复杂度就优化为 O(mn)。

细节

当 i=0 时，f[i-1][..] 均为不合法状态，我们需要直接计算出它们的值，即 f[0][j] = \textit{points}[0][j]。

同时我们可以发现，在状态转移方程中 f[i][..] 只会从 f[i-1][..] 转移而来，因此我们可以使用两个一维数组代替二维数组 f 进行状态转移。此时，我们可以无需特殊考虑 i=0 时所有 f[i][..] 的值。假设我们用来转移的两个数组为 t_1 和 t_2，当 i=0 时，我们使用 t_1 对 t_2 进行转移。由于 t_1 的所有元素均为初始化的 0 值，那么 t_2[j] 一定是从同下标的 t_1[j] 转移而来的（此时 |j-j’| 的值最小），因此可以得到正确的 t_2[j] = \textit{points}[0][j]。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    long long maxPoints(vector<vector<int>>& points) {
        int m = points.size();
        int n = points[0].size();
        vector<long long> f(n);
        for (int i = 0; i < m; ++i) {
            vector<long long> g(n);
            long long best = LLONG_MIN;
            // 正序遍历
            for (int j = 0; j < n; ++j) {
                best = max(best, f[j] + j);
                g[j] = max(g[j], best + points[i][j] - j);
            }
            best = LLONG_MIN;
            // 倒序遍历
            for (int j = n - 1; j >= 0; --j) {
                best = max(best, f[j] - j);
                g[j] = max(g[j], best + points[i][j] + j);
            }
            f = move(g);
        }
        return *max_element(f.begin(), f.end());
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        m, n = len(points), len(points[0])
        f = [0] * n
        for i in range(m):
            g = [0] * n
            best = float("-inf")
            # 正序遍历
            for j in range(n):
                best = max(best, f[j] + j)
                g[j] = max(g[j], best + points[i][j] - j)
            
            best = float("-inf")
            # 倒序遍历
            for j in range(n - 1, -1, -1):
                best = max(best, f[j] - j)
                g[j] = max(g[j], best + points[i][j] + j)
            
            f = g
        
        return max(f)

复杂度分析

  • 时间复杂度：O(mn)。

  • 空间复杂度：O(n)。

 Comments
On this page
1937-扣分后的最大得分