1943-描述绘画结果

给你一个细长的画，用数轴表示。这幅画由若干有重叠的线段表示，每个线段有 独一无二 的颜色。给你二维整数数组 segments ，其中
segments[i] = [starti, endi, colori] 表示线段为 半开区间 [starti, endi) 且颜色为
colori 。

线段间重叠部分的颜色会被 混合 。如果有两种或者更多颜色混合时，它们会形成一种新的颜色，用一个 集合 表示这个混合颜色。

• 比方说，如果颜色 2 ，4 和 6 被混合，那么结果颜色为 {2,4,6} 。

为了简化题目，你不需要输出整个集合，只需要用集合中所有元素的 和 来表示颜色集合。

你想要用 最少数目 不重叠 半开区间 来 表示 这幅混合颜色的画。这些线段可以用二维数组 painting 表示，其中
painting[j] = [leftj, rightj, mixj] 表示一个 半开区间[leftj, rightj) 的颜色
和 为 mixj 。

• 比方说，这幅画由 segments = [[1,4,5],[1,7,7]] 组成，那么它可以表示为 painting = [[1,4,12],[4,7,7]] ，因为：
  • [1,4) 由颜色 {5,7} 组成（和为 12），分别来自第一个线段和第二个线段。
  • [4,7) 由颜色 {7} 组成，来自第二个线段。

请你返回二维数组 painting ，它表示最终绘画的结果（ 没有 被涂色的部分不出现在结果中）。你可以按 任意顺序
返回最终数组的结果。

**半开区间 **[a, b) 是数轴上点 a 和点 b 之间的部分， 包含 点 a 且 不包含 点 b 。

示例 1：

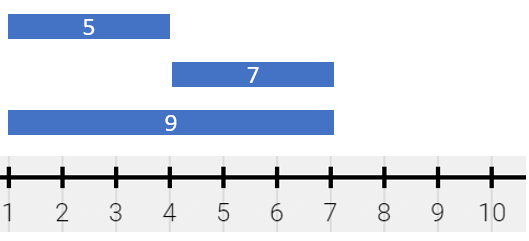
**输入：** segments = [[1,4,5],[4,7,7],[1,7,9]]
**输出：** [[1,4,14],[4,7,16]]
**解释：** 绘画结果可以表示为：
- [1,4) 颜色为 {5,9} （和为 14），分别来自第一和第二个线段。
- [4,7) 颜色为 {7,9} （和为 16），分别来自第二和第三个线段。

示例 2：

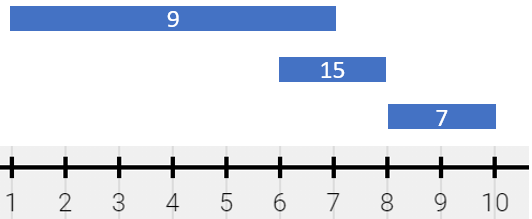
**输入：** segments = [[1,7,9],[6,8,15],[8,10,7]]
**输出：** [[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
**解释：** 绘画结果可以以表示为：
- [1,6) 颜色为 9 ，来自第一个线段。
- [6,7) 颜色为 {9,15} （和为 24），来自第一和第二个线段。
- [7,8) 颜色为 15 ，来自第二个线段。
- [8,10) 颜色为 7 ，来自第三个线段。

示例 3：

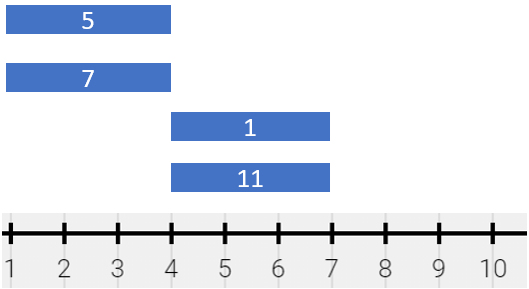
**输入：** segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
**输出：** [[1,4,12],[4,7,12]]
**解释：** 绘画结果可以表示为：
- [1,4) 颜色为 {5,7} （和为 12），分别来自第一和第二个线段。
- [4,7) 颜色为 {1,11} （和为 12），分别来自第三和第四个线段。
注意，只返回一个单独的线段 [1,7) 是不正确的，因为混合颜色的集合不相同。

提示：

• 1 <= segments.length <= 2 * 104
• segments[i].length == 3
• 1 <= starti < endi <= 105
• 1 <= colori <= 109
• 每种颜色 colori 互不相同。

方法一：差分 + 前缀和

思路与算法

由于每条线段的起止点均为整数，因此我们可以在位置 k 处记录数轴上单位长度区间 [k, k + 1) 的颜色和，这样每条线段都覆盖了若干个连续的整数坐标。为了得到数轴上每个整数的颜色和，我们需要将每个线段对数轴的影响叠加。一般的做法是，对于线段覆盖的每个整数，我们都将该整数的颜色和加上线段对应的值。

但这样的做法时间复杂度较高。因此我们可以维护每个线段对于数轴颜色和的变化量。对于每个位置为 [l, r)，颜色为 c 的线段，它对于数轴颜色和的影响体现在两个部分：

• l 相对于 l - 1 的颜色和增加 c；

• r 相对于 r - 1 的颜色和减少 c。

一般我们可以用数轴中整数位置对应的数组（又称差分数组）来维护颜色和变化量。但此处由于颜色和对应的颜色集合可能有很多种，使得即使出现某个边界点颜色和变化量为 0，其两侧的颜色也会不同。

因此，我们使用哈希表来维护所有线段产生的变化量，在数轴上的位置对应哈希表的键，变化量对应哈希表的值。在遍历完所有线段后，我们将这些键值对按照在数轴上的位置升序排序。对于排序后的键值对，我们遍历这些键值对并对颜色和求解前缀和，就可以得出数轴上的颜色和分布。

为了返回数轴的绘画结果，我们需要记录每个颜色和对应的区间，即当前键值对位置与下一个键值对位置组成的左闭右开区间。我们用数组按照格式记录这些区间中颜色和不为零的区间，并最终返回作为答案。

另外，由于每个位置的颜色和变化量和最终的颜色和可能会超出 32 位有符号整数的上界，因此我们需要用 64 位整数存储这些值。

代码

[sol1-C++]

class Solution {
public:
    vector<vector<long long>> splitPainting(vector<vector<int>>& segments) {
        // 计算每个位置对应的颜色和改变量并用哈希表存储
        unordered_map<int, long long> color;
        for (auto&& segment : segments){
            int l = segment[0];
            int r = segment[1];
            int c = segment[2];
            if (!color.count(l)){
                color[l] = 0;
            }
            color[l] += c;
            if (!color.count(r)){
                color[r] = 0;
            }
            color[r] -= c;
        }
        // 将哈希表转化为数组并按数轴坐标升序排序
        vector<pair<int, long long>> axis;
        for (auto&& [k, v] : color){
            axis.emplace_back(k, v);
        }
        sort(axis.begin(), axis.end());
        // 对数组求前缀和计算对应颜色和
        int n = axis.size();
        for (int i = 1; i < n; ++i){
            axis[i].second += axis[i-1].second;
        }
        // 遍历数组生成最终绘画结果
        vector<vector<long long>> res;
        for (int i = 0; i < n - 1; ++i){
            if (axis[i].second){
                res.emplace_back(vector<long long> {axis[i].first, axis[i+1].first, axis[i].second});
            }
        }
        return res;
    }
};

[sol1-Python3]

from collections import defaultdict

class Solution:
    def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:
        # 计算每个位置对应的颜色和改变量并用哈希表存储
        color = defaultdict(lambda: 0)
        for l, r, c in segments:
            color[l] += c
            color[r] -= c
        # 将哈希表转化为数组并按数轴坐标升序排序
        axis = sorted([[k, v] for k, v in color.items()])
        # 对数组求前缀和计算对应颜色和
        n = len(axis)
        for i in range(1, n):
            axis[i][1] += axis[i-1][1]
        # 遍历数组生成最终绘画结果
        res = []
        for i in range(n - 1):
            if axis[i][1]:
                res.append([axis[i][0], axis[i+1][0], axis[i][1]])
        return res

复杂度分析

• 时间复杂度：O(n\log n)，其中 n 为线段的数量。维护变化量哈希表的时间复杂度为 O(n)，将哈希表转化为数组并排序的时间复杂度为 O(n\log n)，遍历数组求前缀和并生成返回数组的时间复杂度为 O(n)。

• 空间复杂度：O(n)，即为存储变化量的哈希表和数组的空间开销。