1948-删除系统中的重复文件夹
由于一个漏洞,文件系统中存在许多重复文件夹。给你一个二维数组 paths,其中 paths[i] 是一个表示文件系统中第 i
个文件夹的绝对路径的数组。
- 例如,
["one", "two", "three"]表示路径"/one/two/three"。
如果两个文件夹(不需要在同一层级)包含 非空且 **相同的 **子文件夹 集合
并具有相同的子文件夹结构,则认为这两个文件夹是相同文件夹。相同文件夹的根层级 不 需要相同。如果存在两个(或两个以上) 相同
文件夹,则需要将这些文件夹和所有它们的子文件夹 标记 为待删除。
- 例如,下面文件结构中的文件夹
"/a"和"/b"相同。它们(以及它们的子文件夹)应该被 全部 标记为待删除:/a/a/x/a/x/y/a/z/b/b/x/b/x/y/b/z
- 然而,如果文件结构中还包含路径
"/b/w",那么文件夹"/a"和"/b"就不相同。注意,即便添加了新的文件夹"/b/w",仍然认为"/a/x"和"/b/x"相同。
一旦所有的相同文件夹和它们的子文件夹都被标记为待删除,文件系统将会 删除
所有上述文件夹。文件系统只会执行一次删除操作。执行完这一次删除操作后,不会删除新出现的相同文件夹。
返回二维数组 __ans ,该数组包含删除所有标记文件夹之后剩余文件夹的路径。路径可以按 任意顺序 返回。
示例 1:
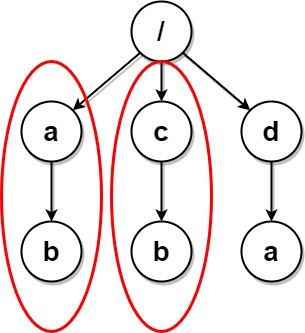
**输入:** paths = [["a"],["c"],["d"],["a","b"],["c","b"],["d","a"]]
**输出:** [["d"],["d","a"]]
**解释:** 文件结构如上所示。
文件夹 "/a" 和 "/c"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "b" 的空文件夹。
示例 2:
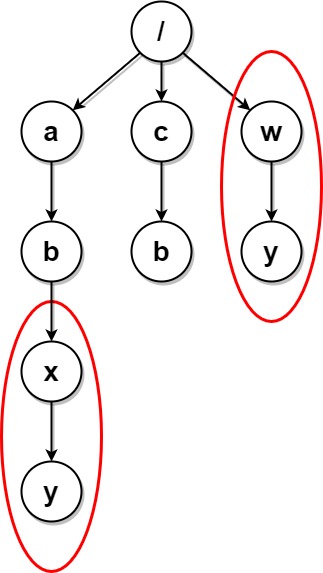
**输入:** paths = [["a"],["c"],["a","b"],["c","b"],["a","b","x"],["a","b","x","y"],["w"],["w","y"]]
**输出:** [["c"],["c","b"],["a"],["a","b"]]
**解释:** 文件结构如上所示。
文件夹 "/a/b/x" 和 "/w"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
注意,文件夹 "/a" 和 "/c" 在删除后变为相同文件夹,但这两个文件夹不会被删除,因为删除只会进行一次,且它们没有在删除前被标记。
示例 3:
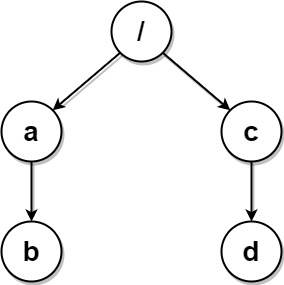
**输入:** paths = [["a","b"],["c","d"],["c"],["a"]]
**输出:** [["c"],["c","d"],["a"],["a","b"]]
**解释:** 文件系统中所有文件夹互不相同。
注意,返回的数组可以按不同顺序返回文件夹路径,因为题目对顺序没有要求。
示例 4:
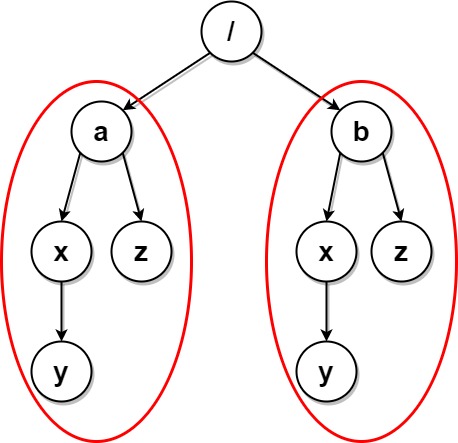
**输入:** paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"]]
**输出:** []
**解释:** 文件结构如上所示。
文件夹 "/a/x" 和 "/b/x"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
文件夹 "/a" 和 "/b"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含一个名为 "z" 的空文件夹以及上面提到的文件夹 "x" 。
示例 5:
**输入:** paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"],["b","w"]]
**输出:** [["b"],["b","w"],["b","z"],["a"],["a","z"]]
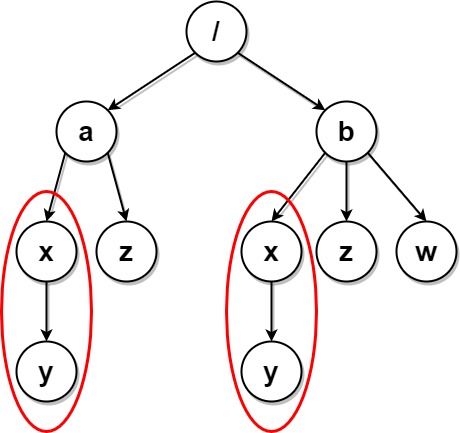
**解释:** 本例与上例的结构基本相同,除了新增 "/b/w" 文件夹。
文件夹 "/a/x" 和 "/b/x" 仍然会被标记,但 "/a" 和 "/b" 不再被标记,因为 "/b" 中有名为 "w" 的空文件夹而 "/a" 没有。
注意,"/a/z" 和 "/b/z" 不会被标记,因为相同子文件夹的集合必须是非空集合,但这两个文件夹都是空的。
提示:
1 <= paths.length <= 2 * 1041 <= paths[i].length <= 5001 <= paths[i][j].length <= 101 <= sum(paths[i][j].length) <= 2 * 105path[i][j]由小写英文字母组成- 不会存在两个路径都指向同一个文件夹的情况
- 对于不在根层级的任意文件夹,其父文件夹也会包含在输入中
方法一:子树的序列化表示
思路
我们可以想出这道题在抽象层面(也就是省去了所有实现细节)的解决方法,即:
第一步,我们通过给定的 paths,简历出文件系统的树型表示。这棵树是一棵多叉树,根节点为 /,每个非根节点表示一个文件夹。
第二步,我们对整棵树从根节点开始进行一次遍历。根据题目中的描述,如果两个节点 x 和 y 包含的子文件夹的「结构」(即这些子文件夹、子文件夹的子文件夹等等,递归直到空文件夹为止)完全相同,我们就需要将 x 和 y 都进行删除。那么,为了得到某一个节点的子文件夹的「结构」,我们应当首先遍历完成该节点的所有子节点,再回溯遍历该节点本身。这就对应着多叉树的后序遍历。
在回溯到某节点时,我们需要将该节点的「结构」存储下来,记录在某一「数据结构」中,以便于与其它节点的「结构」进行比较。
第三步,我们再次对整棵树从根节点开始进行一次遍历。当我们遍历到节点 x 时,如果 x 的「结构」在「数据结构」中出现了超过 1 次,那就说明存在于 x 相同的文件夹,我们就需要将 x 删除并回溯,否则 x 是唯一的,我们将从根节点开始到 x 的路径计入答案,并继续向下遍历 x 的子节点。
在遍历完成后,我们就删除了所有重复的文件夹,并且得到了最终的答案。
算法
对于上面的三个步骤,我们依次尝试进行解决。
对于第一步而言,我们只需要定义一个表示树结构的类,建立一个根节点,随后遍历 paths 中的每一条表示文件夹的路径,将路径上的所有节点加入树中即可。如果读者已经掌握了字典树(Trie)这一数据结构,就可以较快地实现这一步。
对于第二步而言,难点不在于对树进行后序遍历,而在于如何表示一个节点的「结构」。我们可以参考「297. 二叉树的序列化与反序列化」 ,实现一个多叉树的序列化表示。我们用 serial}(x) 记录节点 x 的序列化表示,具体地:
如果节点 x 是子节点,那么 serial}(x) 为空字符串,这是因为节点 x 中不包含任何文件夹,它没有「结构」。例如示例 1 中,三个叶节点 b, a, a 对应的序列化表示均为空字符串;
如果节点 x 不是子节点,它的子节点分别为 y_1, y_2, \cdots, y_k 那么 serial}(x) 递归定义为:
\text{serial}(x) = y_1(\text{serial}(y_1))y_2(\text{serial}(y_2))\cdots y_k(\text{serial}(y_k))
也就是说,我们首先递归地求出 y_1, y_2, \cdots, y_k 的序列化表示,随后将它们连通本身的文件夹名拼接在一起,并在外层使用括号 () 将它们之间进行区分(或者说隔离)。但如果只是随意地进行拼接,会产生顺序的问题,即如果有节点 x_1 和 x_2,它们有相同的子节点 y_1 和 y_2,但在 x_1 的子节点中 y_1 先出现 y_2 后出现,而在 x_2 的子节点中 y_2 先出现而 y_1 后出现,这样尽管 x_1 和 x_2 的「结构」是完全相同的,但会因为子节点的出现顺序不同,导致序列化的字符串不同。
因此,在将 y_1, y_2, \cdots, y_k 的序列化表示进行拼接之前,我们可以对它们进行排序(字典序顺序),再将排序后的结果进行拼接,就可以保证具有相同「结构」的节点的序列化表示是完全相同的了。例如示例 4 中,根节点下方的两个子节点 a, b,它们的序列化表示均为 x(y())z()。
这样一来,通过一次树的后序遍历,我们就可以求出每一个节点「结构」的序列化表示。由于序列化表示都是字符串,因此我们可以使用一个哈希映射,记录每一种序列化表示以及其对应的出现次数。
对于第三步而言,我们从根节点开始对树进行深度优先遍历,并使用一个数组 path 记录从根节点到当前遍历到的节点 x 的路径。如果 x 的序列化表示在哈希映射中出现了超过 1 次,就进行回溯,否则将 path 加入答案,并向下递归遍历 x 的所有子节点。
代码
下面的 C++ 代码没有析构树的空间。如果在面试中遇到了本题,可以和面试官进行沟通,询问是否需要析构对应的空间。
1 | struct Trie { |
1 | class Trie: |
复杂度分析
这里我们只考虑计算所有节点结构的序列化表示需要的时间,以及哈希映射需要使用的空间。对于其它的项(无论是时间项还是空间项),它们在渐近意义下一定都小于计算以及存储序列化表示的部分,因此可以忽略。
在最坏情况下,节点结构的序列化表示的字符串两两不同,那么需要的时间和空间级别均为「所有节点结构的序列化表示的字符串的长度之和」。如何求出这个长度之和的上界呢?
这里我们需要用到一个很重要的结论:
设 T 为无权多叉树。对于 T 中的节点 x,记 dist}[x] 为从根节点到 x 经过的节点个数,size}[x] 为以 x 为根的子树的大小,那么有:
\sum_{x \in T} \textit{dist}[x] = \sum_{x \in T} \textit{size}[x]
证明也较为直观。对于任意的节点 x’,在右侧的 \sum_{x \in T} \textit{size}[x] 中,x’ 被包含在 size}[x] 中的次数就等于 x’ 的祖先节点的数目(也包括 x’ 本身),其等于根节点到 x’ 的经过的节点个数,因此得证。
回到本题,path 中给出了根节点到所有节点的路径,其中最多包含 2\times 10^5 个字符,那么 \sum_{x \in T} \textit{dist}[x] 不超过 2\times 10^5,\sum_{x \in T} \textit{size}[x] 同样也不超过 2\times 10^5。
对于任意的节点 x,x 结构的序列化表示的字符串长度包含两部分,第一部分为其中所有子文件夹名的长度之和,其不超过 10 \cdot \textit{size}[x],第二部分为额外添加的用来区分的括号,由于一个子文件夹会恰好被添加一对括号,因此其不超过 2 \cdot \textit{size}[x]。这样一来,「所有节点结构的序列化表示的字符串的长度之和」的上界为:
12 \cdot \sum_{x \in T} \textit{size}[x] = 2.4 \times 10^6
即空间的数量级为 10^6。而对于时间,即使算上排序的额外 \log 的时间复杂度,也在 10^7 的数量级,可以在规定的时间内通过本题。并且需要指出的是,在上述估算上界的过程中,我们作出的许多假设是非常极端的,因此实际上该方法的运行时间很快。