1954-收集足够苹果的最小花园周长
给你一个用无限二维网格表示的花园, 每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。
你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。
给你一个整数 neededApples ,请你返回土地的 最小周长 ,使得 至少 有 ** **neededApples
个苹果在土地 里面或者边缘上 。
|x| 的值定义为:
- 如果
x >= 0,那么值为x - 如果
x < 0,那么值为-x
示例 1:
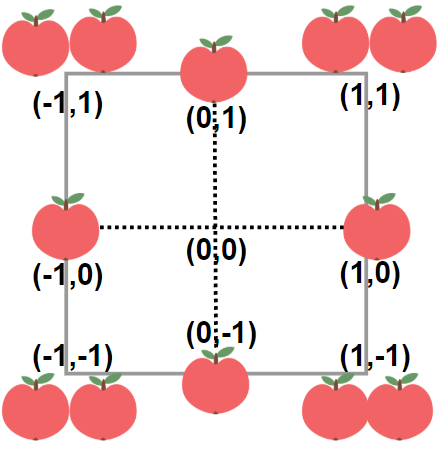
**输入:** neededApples = 1
**输出:** 8
**解释:** 边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果(如上图所示)。
周长为 2 * 4 = 8 。
示例 2:
**输入:** neededApples = 13
**输出:** 16
示例 3:
**输入:** neededApples = 1000000000
**输出:** 5040
提示:
1 <= neededApples <= 1015
方法一:枚举
提示 1
如果正方形土地的右上角坐标为 (n, n),即边长为 2n,周长为 8n,那么其中包含的苹果总数为:
S_n = 2n(n+1)(2n+1)
提示 1 解释
对于坐标为 (x, y) 的树,它有 |x| + |y| 个苹果。因此,一块右上角坐标为 (n, n) 的正方形土地包含的苹果总数为:
S_n = \sum_{x=-n}^n \sum_{y=-n}^n |x| + |y|
由于 x 和 y 是对称的,因此:
\begin{aligned}
S_n &= 2 \sum_{x=-n}^n \sum_{y=-n}^n |x| \
&= 2 \sum_{x=-n}^n (2n+1) |x| \
&= 2(2n+1) \sum_{x=-n}^n |x| \
&= 2n(n+1)(2n+1)
\end{aligned}
思路与算法
我们从小到大枚举 n,直到 2n(n+1)(2n+1) \geq \textit{neededApples 为止。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(m^{1/3}),其中 m 表示题目中的 neededApples。可以发现,S_n 是关于 n 的三次函数,因此需要枚举的 n 的数量级为 O(m^{1/3})。
空间复杂度:O(1)。
方法二:二分查找
思路与算法
由于 S_n 是随着 n 单调递增的,那么我们可以通过二分查找的方法,找出最小的满足 S_n \geq \textit{neededApples 的 n 值即为答案。
细节
二分查找的下界可以直接置为 1,而上界 right 需要保证有 S_\textit{right} \geq \textit{neededApples。根据方法一,我们只需要令 right} = \lfloor \textit{neededApples}^{1/3} \rfloor 即可,其中 \lfloor \cdot \rfloor 表示向下取整。但由于大部分语言中立方根运算较难实现,在实际的编码中,我们可以取一个更加宽松的上界,例如 neededApples}^{1/3 最大值 10^{15 的立方根 10^5。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(\log m),其中 m 表示题目中的 neededApples,即为二分查找需要的时间。
空间复杂度:O(1)。