1975-最大方阵和
给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 :
- 选择
matrix中 相邻 两个元素,并将它们都 乘以-1。
如果两个元素有 公共边 ,那么它们就是 相邻 的。
你的目的是 最大化 方阵元素的和。请你在执行以上操作之后,返回方阵的 最大 和。
示例 1:
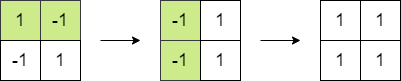
**输入:** matrix = [[1,-1],[-1,1]]
**输出:** 4
**解释:** 我们可以执行以下操作使和等于 4 :
- 将第一行的 2 个元素乘以 -1 。
- 将第一列的 2 个元素乘以 -1 。
示例 2:
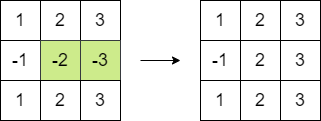
**输入:** matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
**输出:** 16
**解释:** 我们可以执行以下操作使和等于 16 :
- 将第二行的最后 2 个元素乘以 -1 。
提示:
n == matrix.length == matrix[i].length2 <= n <= 250-105 <= matrix[i][j] <= 105
方法一:贪心
提示 1
为了使得操作后方阵总和最大,我们需要使得负数元素的总和尽可能大。
对于方阵中的两个负数元素,一定存在一系列的操作使得这两个负数元素均变为正数,且其余元素不变。
对于方阵中的一个正数元素和一个负数元素,一定存在一系列的操作使得这两个元素交换正负,且其余元素不变。
提示 1 解释
第一部分是显然的。
对于第二部分,我们可以任意选择一条连接两个负数元素的有向路径,按顺序对路径上(除终点以外)的每个元素和它对应的下一个元素都执行一次操作。最终路径上除了两个端点以外的其他元素都被执行了两次操作,因此数值不变;两个端点元素都被执行了一次操作二变为正数。
由于方阵是网格,因此上述路径一定存在。
对于第三部分,将第二部分中的一个负数更改为正数即可证明。
提示 2
如果方阵中存在一个元素为 0,另一个元素为负数。那么一定存在一系列的操作使得负数元素变为正数,且其余元素不变。
提示 2 解释
类似 提示 1,将一个负数元素更改为 0 即可证明。
提示 3
如果方阵中存在 0,那么一定可以通过一系列的操作使得方阵中所有元素均为非负数;
如果方阵中不存在 0,那么:
如果方阵中有奇数个负数元素,那么一定可以通过一系列的操作使得方阵中只有一个负数元素,且该负数元素可以在任何位置。同时,无论如何操作,方阵中必定存在负数元素。
如果方阵中有偶数个负数元素,那么一定可以通过一系列的操作使得方阵中不存在负数元素。
提示 3 解释
对于第一部分,反复对 0 和负数元素进行 提示 2 的操作即可。
对于第二部分,我们首先可以证明如果方阵不存在 0,那么负数元素数量的奇偶性不会改变。然后,我们可以根据 提示 1 构造出一系列操作从而达到对应的要求。
思路与算法
根据 提示 3,我们可以按照方阵的元素分为以下几种情况:
方阵中有 0,那么最大方阵和即为所有元素的绝对值之和;
方阵中没有 0,且负数元素数量为偶数,那么最大方阵和即为所有元素的绝对值之和;
方阵中没有 0,且负数元素数量为奇数,那么最大方阵和即为所有元素的绝对值之和减去所有元素最小绝对值的两倍。
其中,第一种情况也可以按照负数元素数量的奇偶性划入后两种情况中(此时最小绝对值一定为 0)。
我们遍历方阵,维护负数元素的数量、元素的最小绝对值以及所有元素的绝对值之和。随后,我们按照负数元素数量的奇偶性计算对应的最大元素和并返回。
最后,矩阵所有元素绝对值之和可能超过 32 位整数的上限,因此对于 C++ 等语言,需要使用 64 位整数来维护。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(mn),其中 m 为 matrix 的行数,n 为 matrix 的列数。
空间复杂度:O(1)。