1981-最小化目标值与所选元素的差
给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。
从矩阵的 每一行 中选择一个整数,你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。
返回 最小的绝对差 。
a 和 b 两数字的 绝对差 是 a - b 的绝对值。
示例 1:
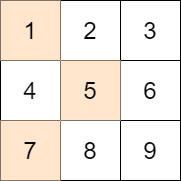
**输入:** mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
**输出:** 0
**解释:** 一种可能的最优选择方案是:
- 第一行选出 1
- 第二行选出 5
- 第三行选出 7
所选元素的和是 13 ,等于目标值,所以绝对差是 0 。
示例 2:

**输入:** mat = [[1],[2],[3]], target = 100
**输出:** 94
**解释:** 唯一一种选择方案是:
- 第一行选出 1
- 第二行选出 2
- 第三行选出 3
所选元素的和是 6 ,绝对差是 94 。
示例 3:

**输入:** mat = [[1,2,9,8,7]], target = 6
**输出:** 1
**解释:** 最优的选择方案是选出第一行的 7 。
绝对差是 1 。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 701 <= mat[i][j] <= 701 <= target <= 800
方法一:背包型动态规划
思路与算法
我们用 f[i][j] 表示在矩阵 mat 的第 0, 1, \cdots, i 行分别选择一个整数,是否存在一种和为 j 的方案。在进行状态转移时,我们枚举第 i 行的每一个数 x,那么除去第 i 行的和即为 j-x,因此有状态转移方程:
f[i][j] \leftarrow f[i-1][j-x]
这里的 \leftarrow 表示转移方向。由于 f[i][j] 表示的是「存在性」,因此如果 f[i-1][j-x] 的值为 true,那么将 f[i][j] 更新为 true,否则 f[i][j] 保持不变。换句话说,也就是:
f[i][j] = f[i][j] \vee f[i-1][j-x]
这里的 \vee 表示逻辑或运算。
在动态规划完成后,我们遍历所有的 f[m-1][..],如果其中的某一项 f[m-1][j] 的值为 true,那么说明存在一种和为 j 的方案,我们用 |j - \textit{target}| 更新最终的答案即可。
细节
这里的细节较多,希望读者认真阅读和思考。
首先我们要确定在动态规划时 j 的枚举范围。在对第 i 行进行动态规划时,我们可以使用一个变量 maxsum 存储第 0, 1, \cdots, i-1 行的每一行的最大值之和。这样一来,对于第 i 行的数 x,j 的枚举范围就是 [x, \textit{maxsum} + x]。
在状态转移方程中,我们发现 f[i][j] 只会从 f[i-1][..] 转移而来,因此我们可以使用两个一维数组代替该二维数组进行动态规划。需要注意的是,在对第 i 行进行动态规划时,表示第 i-1 行的数组至少需要长度 maxsum} + 1,而表示第 i 行的数组在此基础上需要额外的「第 i 行的最大值」的长度,这样才能使得到第 i-1 行为止以及到第 i 行为止的最大值之和都不超过数组的边界。
当然,我们也可以直接将数组的长度固定为 4900。题目中 m 的最大值和数组元素的最大值均为 70,因此最大值之和不会超过 4900。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(m^2nC),其中 C 是数组 mat 中的元素最大值。这个时间复杂度很容易超出时间限制(特别是对于一些解释性语言)。因此可以考虑将动态规划的数组换成哈希表,具体可以参考上面的 Python 代码。
空间复杂度:O(mC),即为动态规划中数组(或哈希表)需要的空间。
方法二:使用 target 进行优化
思路与算法
方法一没有很好地利用题目中 target 范围的限制。target 的最大值为 800,而全部的 m 行的最大值之和最大为 4900,远远大于前者。这样就造成了许多不必要的状态转移。
由于我们的目标是最小化「和」与 target 的差值的「绝对值」,因此当「和」已经大于等于 target 时,我们再增大「和」显然是没有必要的。
因此,在状态转移的过程中,我们只需要使用长度为 target 的数组存储所有小于 target 的和,此外再使用一个变量 large 存储最小的大于等于 target 的和。这样一来,我们就可以更快速地进行状态转移。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(mn \cdot \textit{target})。
空间复杂度:O(\textit{target}),即为动态规划中数组(或哈希表)需要使用的空间。