2003-每棵子树内缺失的最小基因值

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:24 2023-09-13 16:06:24 Updated    

有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0
开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ，所以
parents[0] == -1 。

总共有 105 个基因值，每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组
nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 _ _ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小
基因值。

节点 x 为根的 **子树 **包含节点 x 和它所有的 后代 节点。

示例 1：

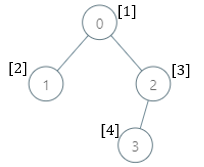
**输入：** parents = [-1,0,0,2], nums = [1,2,3,4]
**输出：** [5,1,1,1]
**解释：** 每个子树答案计算结果如下：
- 0：子树包含节点 [0,1,2,3] ，基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1：子树只包含节点 1 ，基因值为 2 。1 是缺失的最小基因值。
- 2：子树包含节点 [2,3] ，基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3：子树只包含节点 3 ，基因值为 4 。1是缺失的最小基因值。

示例 2：

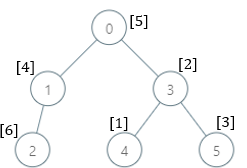
**输入：** parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
**输出：** [7,1,1,4,2,1]
**解释：** 每个子树答案计算结果如下：
- 0：子树内包含节点 [0,1,2,3,4,5] ，基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1：子树内包含节点 [1,2] ，基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2：子树内只包含节点 2 ，基因值为 6 。1 是缺失的最小基因值。
- 3：子树内包含节点 [3,4,5] ，基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4：子树内只包含节点 4 ，基因值为 1 。2 是缺失的最小基因值。
- 5：子树内只包含节点 5 ，基因值为 3 。1 是缺失的最小基因值。

示例 3：

**输入：** parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
**输出：** [1,1,1,1,1,1,1]
**解释：** 所有子树都缺失基因值 1 。

提示：

  • n == parents.length == nums.length
  • 2 <= n <= 105
  • 对于 i != 0 ，满足 0 <= parents[i] <= n - 1
  • parents[0] == -1
  • parents 表示一棵合法的树。
  • 1 <= nums[i] <= 105
  • nums[i] 互不相同。

解法一：启发式合并

遍历整棵树，统计每棵子树包含的基因值集合，以及缺失的最小基因值（记作 mex）。合并基因值集合时，总是从小的往大的合并（类似并查集的按秩合并），同时更新当前子树的 mex 的最大值。合并完成后再不断自增子树的 mex 直至其不在基因值集合中。

这一方法同时也适用于有相同基因值的情况。

时间复杂度：O(n\log n)。证明 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(parents)
	g := make([][]int, n)
	for w := 1; w < n; w++ {
		v := parents[w]
		g[v] = append(g[v], w)
	}
	mex := make([]int, n)
	var f func(int) map[int]bool
	f = func(v int) map[int]bool {
		inSet := map[int]bool{}
		mex[v] = 1
		for _, w := range g[v] {
			s := f(w)
			// 启发式合并：保证从小的集合合并到大的集合
			if len(s) > len(inSet) {
				inSet, s = s, inSet
			}
			for x := range s {
				inSet[x] = true
			}
			if mex[w] > mex[v] {
				mex[v] = mex[w]
			}
		}
		inSet[nums[v]] = true
		for inSet[mex[v]] {
			mex[v]++ // 不断自增直至 mex[v] 不在集合中
		}
		return inSet
	}
	f(0)
	return mex
}

解法二：利用无重复基因值的性质

由于没有重复基因，若存在一个节点 x，其基因值为 1，那么从 x 到根这一条链上的所有节点，由于子树包含 x，其 mex 均大于 1，而其余不在链上的节点，由于子树不包含 x，故其 mex 均为 1。因此，我们只需要计算在这条链上的节点的 mex 值。

我们可以从 x 出发，顺着父节点往根走，同时收集当前子树下的所有基因值，然后再不断自增子树的 mex 直至其不在基因值集合中。

时间复杂度：O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(parents)
	mex := make([]int, n)
	for i := range mex {
		mex[i] = 1
	}

	g := make([][]int, n)
	for w := 1; w < n; w++ {
		v := parents[w]
		g[v] = append(g[v], w)
	}

	inSet := map[int]bool{}
	var f func(int)
	f = func(v int) {
		inSet[nums[v]] = true // 收集基因值
		for _, w := range g[v] {
			if !inSet[nums[w]] { // 避免重复访问节点
				f(w)
			}
		}
	}

	// 找到基因值等于 1 的节点 x
	x := -1
	for i, v := range nums {
		if v == 1 {
			x = i
			break
		}
	}
	// x 顺着父节点往上走
	for cur := 2; x >= 0; x = parents[x] {
		f(x)
		for inSet[cur] {
			cur++ // 不断自增直至不在基因值集合中
		}
		mex[x] = cur
	}
	return mex
}
 Comments
On this page
2003-每棵子树内缺失的最小基因值