2033-获取单值网格的最小操作数

给你一个大小为 m x n 的二维整数网格 grid 和一个整数 x 。每一次操作，你可以对 grid 中的任一元素 加 x 或
减 x 。

单值网格 是全部元素都相等的网格。

返回使网格化为单值网格所需的 最小 操作数。如果不能，返回 -1 。

示例 1：

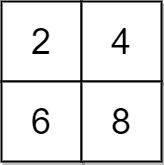
**输入：** grid = [[2,4],[6,8]], x = 2
**输出：** 4
**解释：** 可以执行下述操作使所有元素都等于 4 ： 
- 2 加 x 一次。
- 6 减 x 一次。
- 8 减 x 两次。
共计 4 次操作。

示例 2：

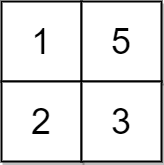
**输入：** grid = [[1,5],[2,3]], x = 1
**输出：** 5
**解释：** 可以使所有元素都等于 3 。

示例 3：

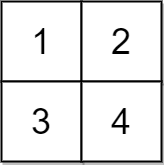
**输入：** grid = [[1,2],[3,4]], x = 2
**输出：** -1
**解释：** 无法使所有元素相等。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= x, grid[i][j] <= 104

要使任意两元素最终相等，这两元素的差必须是 x 的倍数，否则无法通过加减 x 来相等。我们可以以数组中的某一元素为基准，若所有元素与它的差均为 x 的倍数，则任意两元素之差为 x 的倍数。

假设要让所有元素均为 y，设小于 y 的元素有 p 个，大于 y 的元素有 q 个，可以发现：

• 若 p<q，y 每增加 x，操作数就可以减小 q-p；
• 若 p>q，y 每减小 x，操作数就可以减小 p-q；

因此 p=q 时可以让总操作数最小，此时 y 为所有元素的中位数。

func minOperations(grid [][]int, x int) (ans int) {
	n := len(grid) * len(grid[0])
	a := make([]int, 0, n)
	for _, row := range grid {
		for _, v := range row {
			if (v-grid[0][0])%x != 0 { // 以其中一元素为基准，若所有元素与它的差均为 x 的倍数，则任意两元素之差为 x 的倍数
				return -1
			}
		}
		a = append(a, row...)
	}
	sort.Ints(a) // 除了排序，也可以用求第 k 大算法来找中位数
	for _, v := range a {
		ans += abs(v-a[n/2]) / x
	}
	return
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}