2040-两个有序数组的第 K 小乘积

给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ，请你返回第 _
_k （从 1 开始编号）小的 nums1[i] * nums2[j] _ _ 的乘积，其中 _ _0 <= i < nums1.length __ 且 __0 <= j < nums2.length 。

示例 1：

**输入：** nums1 = [2,5], nums2 = [3,4], k = 2
**输出：** 8
**解释：** 第 2 小的乘积计算如下：
- nums1[0] * nums2[0] = 2 * 3 = 6
- nums1[0] * nums2[1] = 2 * 4 = 8
第 2 小的乘积为 8 。

示例 2：

**输入：** nums1 = [-4,-2,0,3], nums2 = [2,4], k = 6
**输出：** 0
**解释：** 第 6 小的乘积计算如下：
- nums1[0] * nums2[1] = (-4) * 4 = -16
- nums1[0] * nums2[0] = (-4) * 2 = -8
- nums1[1] * nums2[1] = (-2) * 4 = -8
- nums1[1] * nums2[0] = (-2) * 2 = -4
- nums1[2] * nums2[0] = 0 * 2 = 0
- nums1[2] * nums2[1] = 0 * 4 = 0
第 6 小的乘积为 0 。

示例 3：

**输入：** nums1 = [-2,-1,0,1,2], nums2 = [-3,-1,2,4,5], k = 3
**输出：** -6
**解释：** 第 3 小的乘积计算如下：
- nums1[0] * nums2[4] = (-2) * 5 = -10
- nums1[0] * nums2[3] = (-2) * 4 = -8
- nums1[4] * nums2[0] = 2 * (-3) = -6
第 3 小的乘积为 -6 。

提示：

1 <= nums1.length, nums2.length <= 5 * 104
-105 <= nums1[i], nums2[j] <= 105
1 <= k <= nums1.length * nums2.length
nums1 和 nums2 都是从小到大排好序的。

解法框架：二分查找

做过类似题目（668. 乘法表中第k小的数或者 719. 找出第 k 小的距离对）的不难发现这题的解法是二分查找。首先令 f(x) = 满足 nums_1[i] * nums_2[j] \le x 的数对个数，显然 f(x) 是关于 x 递增的，因此可以进行二分查找，找到第一个满足 f(x) \ge k 的 x 即可。

下面的给出三种求 f(x) 的解法。

解法一：双指针 — 分类讨论

在类似题目 668. 乘法表中第k小的数和 719. 找出第 k 小的距离对中，经典的解法是双指针，将单次 check 的时间复杂度降低到了 O(n)。那么这个题目呢？

首先，我们把 nums_1 分成 neg_1 和 pos_1，分别表示 nums_1 的 负数部分 和 非负数部分；
把 nums_2 分成 neg_2 和 pos_2，分别表示 nums_2 的 负数部分 和 非负数部分。

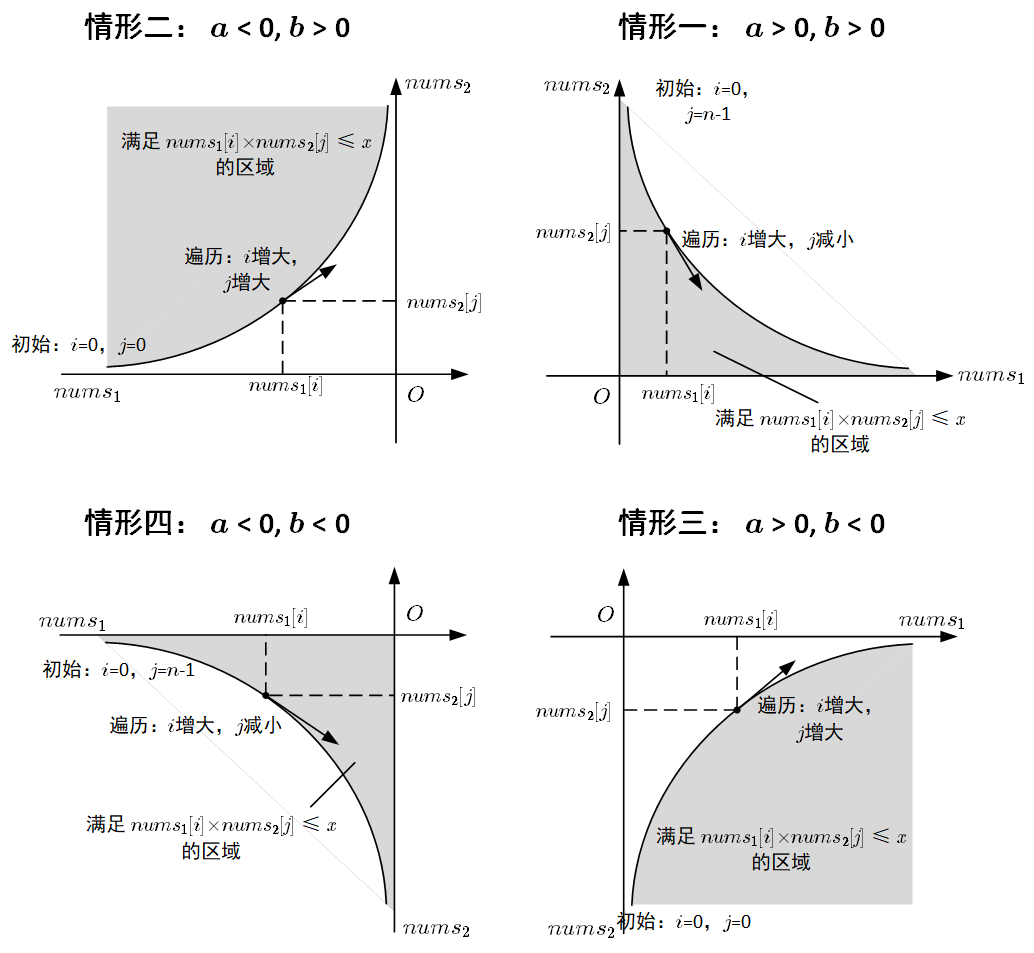
一图胜千言，下面用一幅图来解释双指针遍历的各种边界条件。

情形一：nums_1[i] \ge 0， nums_2[j] \ge 0，分别对应 pos_1 和 pos_2；
情形二：nums_1[i] < 0， nums_2[j] \ge 0，分别对应 neg_1 和 pos_2；
情形三：nums_1[i] \ge 0， nums_2[j] < 0，分别对应 pos_1 和 neg_2；
情形四：nums_1[i] < 0， nums_2[j] < 0，分别对应 neg_1 和 neg_2。

代码

class Solution {
public:
    long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
        vector<int> neg1, pos1, neg2, pos2;
        for(int v : nums1) (v < 0)? neg1.push_back(v) : pos1.push_back(v);
        for(int v : nums2) (v < 0)? neg2.push_back(v) : pos2.push_back(v);

        long long l = -1e10, r = 1e10;
        while(l < r) {
            long long m = (l + r) >> 1;
            long long cur = 0;
            for(int i = 0, j = (int)pos2.size() - 1; i < pos1.size(); ++i) {
                while(j >= 0 && 1ll * pos1[i] * pos2[j] > m) --j;
                cur += j + 1;
            }
            for(int i = 0, j = 0; i < neg1.size(); ++i) {
                while(j < pos2.size() && 1ll * neg1[i] * pos2[j] > m) ++j;
                cur += (int)pos2.size() - j;
            }
            for(int i = 0, j = 0; i < pos1.size(); ++i) {
                while(j < neg2.size() && 1ll * pos1[i] * neg2[j] <= m) ++j;
                cur += j;
            }
            for(int i = 0, j = (int)neg2.size() - 1; i < neg1.size(); ++i) {
                while(j >= 0 && 1ll * neg1[i] * neg2[j] <= m) --j;
                cur += (int)neg2.size() - 1 - j;
            }
            if(cur < k) l = m + 1;
            else r = m;
        }

        return l;
    }
};

如果不想思考那么多复杂的边界条件，那么下面这种双指针方法的思考量较小，可以一试。

解法一点五：双指针 — 等价转换

上面的分类讨论之所以麻烦，关键在于数字有正有负，需要分 4 种情况讨论。如果我们可以将 4 种情况都转化为一种情况呢？
答案是可以。

如果 nums_1[i] < 0, nums_2[j] \ge 0，则 nums_1[i] \times nums_2[j] \le x
等价于 (-nums_1[i]) \times nums_2[j] \ge x
如果 nums_1[i] \ge 0, nums_2[j] < 0，则 nums_1[i] \times nums_2[j] \le x
等价于 nums_1[i] \times (-nums_2[j]) \ge x
如果 nums_1[i] \ge 0, nums_2[j] < 0，则 nums_1[i] \times nums_2[j] \le x
等价于 (-nums_1[i]) \times (-nums_2[j]) \le x

这样我们就将有负数的情形二、三、四转化为全是非负整数的情形一了。注意，由于负数取反后，大小关系发生了逆转，所以需要将数组反转，以保持递增的顺序。

代码

class Solution {
public:
    long long calc(vector<int>& a, vector<int>& b, long long x, bool greater) {
        long long res = 0;
        if(!a.size() || !b.size()) return 0;
        for(int i = 0, j = (int)b.size() - 1, k = (int)b.size() - 1; i < a.size(); ++i) {
            while(j >= 0 && 1ll * a[i] * b[j] > x) --j;
            while(k >= 0 && 1ll * a[i] * b[k] >= x) --k;
            if(greater) res += (int)b.size() - 1 - k;
            else res += j + 1;
        }
        return res;
    }
    long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
        vector<int> neg1, pos1, neg2, pos2;
        for(int v : nums1) (v < 0)? neg1.push_back(-v) : pos1.push_back(v);
        for(int v : nums2) (v < 0)? neg2.push_back(-v) : pos2.push_back(v);
        reverse(neg1.begin(), neg1.end());
        reverse(neg2.begin(), neg2.end());

        long long l = -1e10, r = 1e10;
        while(l < r) {
            long long m = (l + r) >> 1, cur = 0;
            cur += calc(pos1, pos2, m, false);
            cur += calc(neg1, pos2, -m, true);
            cur += calc(pos1, neg2, -m, true);
            cur += calc(neg1, neg2, m, false);
            if(cur < k) l = m + 1;
            else r = m;
        }

        return l;
    }
};

解法二：解不等式 + 嵌套二分查找

我们可以首先在 nums_1 枚举数字 a，然后找出 nums_2 中满足 ab \le x 的数字的 b 的个数即可。

如果 a > 0，则不等式 ab \le x 成立的条件是 \displaystyle{b \le \left\lfloor x}{a} \right\rfloor（向下取整）；

如果 a < 0，则不等式 ab \le x 成立的条件是 \displaystyle{b \ge \left\lceil x}{a} \right\rceil（向上取整）；

a = 0 的情况比较特殊，此时若 x \ge 0，则 ab \le x 恒成立；否则 ab \le x 恒不成立。

由于 nums_2 已经排好序，故我们对于 nums_1 中的每个 a，只需要在 nums_2 中二分查找小于等于（或大于等于）x 的数量即可。

细节 + 小知识

如何实现向下取整呢？直接用整数除法 a/b 不行吗？不幸的是，实际上 C/C++ 的除法实现是 向 0 取整 的。例如 -1 / 2 的值是 0，而不是 -1。因此需要稍微改变一下思路。
思路一：采用浮点数 + floor 库函数实现向下取整；顺带用 ceil 库函数实现向上取整。

long long floorDiv(long long x, long long y) {
    return floor(x / (double)y + 1e-7);
}
long long ceilDiv(long long x, long long y) {
    return ceil(x / (double)y - 1e-7);
}

思路二：避免浮点数运算的实现：

long long floorDiv(long long x, long long y) {
    if(y < 0) x = -x, y = -y;
    if(x < 0) return (x - (y - 1)) / y;
    return x / y;
}
long long ceilDiv(long long x, long long y) {
    if(y < 0) x = -x, y = -y;
    if(x < 0) return x / y;
    return (x + (y - 1)) / y;
}

最终代码

class Solution {
public:
    long long floorDiv(long long x, long long y) {
        if(y < 0) x = -x, y = -y;
        if(x < 0) return (x - (y - 1)) / y;
        return x / y;
    }
    long long ceilDiv(long long x, long long y) {
        if(y < 0) x = -x, y = -y;
        if(x < 0) return x / y;
        return (x + (y - 1)) / y;
    }
    long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
        long long l = -1e10, r = 1e10;
        while(l < r) {
            long long m = (l + r) >> 1;
            long long cur = 0;
            for(int v : nums1) {
                if(v < 0) {
                    cur += nums2.end() - lower_bound(nums2.begin(), nums2.end(), ceilDiv(m, v));
                } else if(v == 0) {
                    cur += (m >= 0)? nums2.size() : 0;
                } else {
                    cur += upper_bound(nums2.begin(), nums2.end(), floorDiv(m, v)) - nums2.begin();
                }
            }
            if(cur < k) l = m + 1;
            else r = m;
        }
        return l;
    }
};

解法三：前缀和

解法二中，我们也可以不用嵌套二分查找。注意到 -10^5 \le nums_1[i], nums_2[i] \le 10^5，我们完全可以开辟足够大的空间来统计 nums_2 中各个数字的数量，然后采用前缀和的方式来统计 nums_2 中 \le x 的数字数目，这样可以免去二分查找。

代码

class Solution {
public:
    long long sums[200005] = {0};
    long long floorDiv(long long x, long long y) {
        if(y < 0) x = -x, y = -y;
        if(x < 0) return (x - (y - 1)) / y;
        return x / y;
    }
    long long ceilDiv(long long x, long long y) {
        if(y < 0) x = -x, y = -y;
        if(x < 0) return x / y;
        return (x + (y - 1)) / y;
    }
    long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
        for(int v : nums2) sums[v + 100000]++;
        for(int i = 1; i <= 200000; ++i) sums[i] += sums[i-1];

        auto sum = [&](long long x) -> long long {
            if(x < -100000) return 0;
            if(x > 100000) return sums[200000];
            return sums[x + 100000];
        };

        long long l = -1e10, r = 1e10;
        while(l < r) {
            long long m = (l + r) >> 1;
            
            long long cnt = 0;
            for(int v : nums1) {
                if(v < 0) cnt += sum(100000) - sum(ceilDiv(m, v) - 1);
                if(v == 0 && m >= 0) cnt += nums2.size();
                if(v > 0) cnt += sum(floorDiv(m, v));
            }

            if(cnt < k) l = m + 1;
            else r = m;
        }

        return l;
    }
};