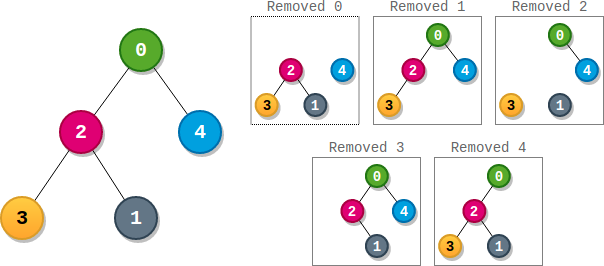
给你一棵根节点为 0 的 二叉树 ,它总共有 n 个节点,节点编号为 0 到 n - 1 。同时给你一个下标从 0 parents 表示这棵树,其中 parents[i] 是节点 i 的父节点。由于节点 0 是根,所以parents[0] == -1 。
一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是,将这个节点和与它相连的边全部删除 ,剩余部分是若干个 非空 子树,这个节点的 分数 为所有这些子树 大小的乘积 。
请你返回有 最高得分 节点的 数目 。
示例 1:
**输入:** parents = [-1,2,0,2,0]
**输出:** 3
**解释:**
- 节点 0 的分数为:3 * 1 = 3
- 节点 1 的分数为:4 = 4
- 节点 2 的分数为:1 * 1 * 2 = 2
- 节点 3 的分数为:4 = 4
- 节点 4 的分数为:4 = 4
最高得分为 4 ,有三个节点得分为 4 (分别是节点 1,3 和 4 )。
示例 2:
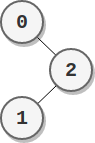
**输入:** parents = [-1,2,0]
**输出:** 2
**解释:**
- 节点 0 的分数为:2 = 2
- 节点 1 的分数为:2 = 2
- 节点 2 的分数为:1 * 1 = 1
最高分数为 2 ,有两个节点分数为 2 (分别为节点 0 和 1 )。
提示:
n == parents.length2 <= n <= 105parents[0] == -1对于 i != 0 ,有 0 <= parents[i] <= n - 1
parents 表示一棵二叉树。
方法一:深度优先搜索 思路
在一棵树中,当把一个节点和与它相连的所有边删除,剩余部分最多为三棵非空子树,即原节点的左子树(如果有),右子树(如果有),以及把以这个节点为根结点的子树移除所形成的子树(除根结点外均有)。而这个节点的分数为这些子树的节点个数的乘积。我们可以先用 parents 数组统计出每个节点的子节点,然后使用深度优先搜索来计算以每个节点为根结点的子树的大小,同时计算每个节点的大小,作为深度优先搜索的返回值,最后统计最大分数出现的次数。在实现上,统计最大分数出现的次数可以放到深度优先搜索中完成,从而节省一部分空间。
代码
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def countHighestScoreNodes (self, parents: List [int ] ) -> int : n = len (parents) children = [[] for _ in range (n)] for node, p in enumerate (parents): if p != -1 : children[p].append(node) maxScore, cnt = 0 , 0 def dfs (node: int ) -> int : score = 1 size = n - 1 for ch in children[node]: sz = dfs(ch) score *= sz size -= sz if node != 0 : score *= size nonlocal maxScore, cnt if score == maxScore: cnt += 1 elif score > maxScore: maxScore, cnt = score, 1 return n - size dfs(0 ) return cnt
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution { long maxScore = 0 ; int cnt = 0 ; int n; List<Integer>[] children; public int countHighestScoreNodes (int [] parents) { n = parents.length; children = new List [n]; for (int i = 0 ; i < n; i++) { children[i] = new ArrayList <Integer>(); } for (int i = 0 ; i < n; i++) { int p = parents[i]; if (p != -1 ) { children[p].add(i); } } dfs(0 ); return cnt; } public int dfs (int node) { long score = 1 ; int size = n - 1 ; for (int c : children[node]) { int t = dfs(c); score *= t; size -= t; } if (node != 0 ) { score *= size; } if (score == maxScore) { cnt++; } else if (score > maxScore) { maxScore = score; cnt = 1 ; } return n - size; } }
[sol1-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class Solution { long maxScore = 0 ; int cnt = 0 ; int n; IList<int >[] children; public int CountHighestScoreNodes (int [] parents n = parents.Length; children = new IList<int >[n]; for (int i = 0 ; i < n; i++) { children[i] = new List<int >(); } for (int i = 0 ; i < n; i++) { int p = parents[i]; if (p != -1 ) { children[p].Add(i); } } DFS(0 ); return cnt; } public int DFS (int node long score = 1 ; int size = n - 1 ; foreach (int c in children[node]) { int t = DFS(c); score *= t; size -= t; } if (node != 0 ) { score *= size; } if (score == maxScore) { cnt++; } else if (score > maxScore) { maxScore = score; cnt = 1 ; } return n - size; } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution {public : long maxScore = 0 ; int cnt = 0 ; int n; vector<vector<int >> children; int dfs (int node) long score = 1 ; int size = n - 1 ; for (int c : children[node]) { int t = dfs (c); score *= t; size -= t; } if (node != 0 ) { score *= size; } if (score == maxScore) { cnt++; } else if (score > maxScore) { maxScore = score; cnt = 1 ; } return n - size; } int countHighestScoreNodes (vector<int >& parents) this ->n = parents.size (); this ->children = vector<vector<int >>(n); for (int i = 0 ; i < n; i++) { int p = parents[i]; if (p != -1 ) { children[p].emplace_back (i); } } dfs (0 ); return cnt; } };
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 int dfs (int node, long * maxScore, int * cnt, int n, const struct ListNode ** children) { long score = 1 ; int size = n - 1 ; for (struct ListNode * curr = children[node]; curr; curr = curr->next) { int t = dfs(curr->val, maxScore, cnt, n, children); score *= t; size -= t; } if (node != 0 ) { score *= size; } if (score == *maxScore) { (*cnt)++; } else if (score > *maxScore) { *maxScore = score; *cnt = 1 ; } return n - size; } int countHighestScoreNodes (int * parents, int parentsSize) { int n = parentsSize; int cnt = 0 ; long maxScore = 0 ; struct ListNode ** children =struct ListNode **)malloc (sizeof (struct ListNode *) * n); for (int i = 0 ; i < n; i++) { children[i] = NULL ; } for (int i = 0 ; i < n; i++) { int p = parents[i]; if (p != -1 ) { struct ListNode * node =struct ListNode *)malloc (sizeof (struct ListNode)); node->val = i; node->next = children[p]; children[p] = node; } } dfs(0 , &maxScore, &cnt, n, children); for (int i = 0 ; i < n; i++) { for (struct ListNode * curr = children[i]; curr; ) { struct ListNode * next = free (curr); curr = next; } } free (children); return cnt; }
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 func countHighestScoreNodes (parents []int ) int ) { n := len (parents) children := make ([][]int , n) for node := 1 ; node < n; node++ { p := parents[node] children[p] = append (children[p], node) } maxScore := 0 var dfs func (int ) int dfs = func (node int ) int { score, size := 1 , n-1 for _, ch := range children[node] { sz := dfs(ch) score *= sz size -= sz } if node > 0 { score *= size } if score == maxScore { ans++ } else if score > maxScore { maxScore = score ans = 1 } return n - size } dfs(0 ) return }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 var countHighestScoreNodes = function (parents ) { const n = parents.length ; const children = new Array (n).fill (0 ); let maxScore = 0 ; let cnt = 0 ; for (let i = 0 ; i < n; i++) { children[i] = []; } for (let i = 0 ; i < n; i++) { const p = parents[i]; if (p !== -1 ) { children[p].push (i); } } const dfs = (node ) => { let score = 1 ; let size = n - 1 ; for (const c of children[node]) { let t = dfs (c); score *= t; size -= t; } if (node !== 0 ) { score *= size; } if (score === maxScore) { cnt++; } else if (score > maxScore) { maxScore = score; cnt = 1 ; } return n - size; } dfs (0 ); return cnt; };
复杂度分析