2056-棋盘上有效移动组合的数目
有一个 8 x 8 的棋盘,它包含 n 个棋子(棋子包括车,后和象三种)。给你一个长度为 n 的字符串数组 pieces ,其中pieces[i] 表示第 i 个棋子的类型(车,后或象)。除此以外,还给你一个长度为 n 的二维整数数组 positions ,其中positions[i] = [ri, ci] 表示第 i 个棋子现在在棋盘上的位置为 (ri, ci) ,棋盘下标从 1 开始。
棋盘上每个棋子都可以移动 至多一次 。每个棋子的移动中,首先选择移动的 方向 ,然后选择 移动的步数
,同时你要确保移动过程中棋子不能移到棋盘以外的地方。棋子需按照以下规则移动:
- 车可以 水平或者竖直 从
(r, c)沿着方向(r+1, c),(r-1, c),(r, c+1)或者(r, c-1)移动。 - 后可以 水平竖直或者斜对角 从
(r, c)沿着方向(r+1, c),(r-1, c),(r, c+1),(r, c-1),(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1)移动。 - 象可以 斜对角 从
(r, c)沿着方向(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1)移动。
移动组合 包含所有棋子的 移动 。每一秒,每个棋子都沿着它们选择的方向往前移动 一步 ,直到它们到达目标位置。所有棋子从时刻0 开始移动。如果在某个时刻,两个或者更多棋子占据了同一个格子,那么这个移动组合 不有效 。
请你返回 有效 移动组合的数目。
注意:
- 初始时, 不会有两个棋子 在 同一个位置 。
- 有可能在一个移动组合中,有棋子不移动。
- 如果两个棋子 直接相邻 且两个棋子下一秒要互相占据对方的位置,可以将它们在同一秒内 交换位置 。
示例 1:
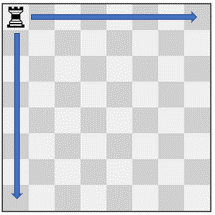
**输入:** pieces = ["rook"], positions = [[1,1]]
**输出:** 15
**解释:** 上图展示了棋子所有可能的移动。
示例 2:
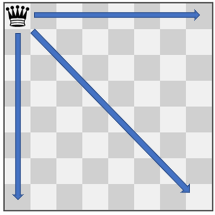
**输入:** pieces = ["queen"], positions = [[1,1]]
**输出:** 22
**解释:** 上图展示了棋子所有可能的移动。
示例 3:
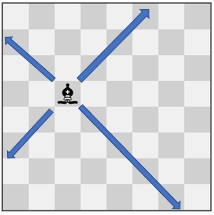
**输入:** pieces = ["bishop"], positions = [[4,3]]
**输出:** 12
**解释:** 上图展示了棋子所有可能的移动。
示例 4:
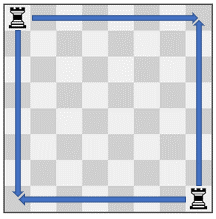
**输入:** pieces = ["rook","rook"], positions = [[1,1],[8,8]]
**输出:** 223
**解释:** 每个车有 15 种移动,所以总共有 15 * 15 = 225 种移动组合。
但是,有两个是不有效的移动组合:
- 将两个车都移动到 (8, 1) ,会导致它们在同一个格子相遇。
- 将两个车都移动到 (1, 8) ,会导致它们在同一个格子相遇。
所以,总共有 225 - 2 = 223 种有效移动组合。
注意,有两种有效的移动组合,分别是一个车在 (1, 8) ,另一个车在 (8, 1) 。
即使棋盘状态是相同的,这两个移动组合被视为不同的,因为每个棋子移动操作是不相同的。
示例 5:

**输入:** pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
**输出:** 281
**解释:** 总共有 12 * 24 = 288 种移动组合。
但是,有一些不有效的移动组合:
- 如果后停在 (6, 7) ,它会阻挡象到达 (6, 7) 或者 (7, 8) 。
- 如果后停在 (5, 6) ,它会阻挡象到达 (5, 6) ,(6, 7) 或者 (7, 8) 。
- 如果象停在 (5, 2) ,它会阻挡后到达 (5, 2) 或者 (5, 1) 。
在 288 个移动组合当中,281 个是有效的。
提示:
n == pieces.lengthn == positions.length1 <= n <= 4pieces只包含字符串"rook","queen"和"bishop"。- 棋盘上总共最多只有一个后。
1 <= xi, yi <= 8- 每一个
positions[i]互不相同。
看到这种题意比较长的题目首先需要理顺题意,然后理顺思路,写起代码就简单了。
题意:
- 棋盘上有 3 种棋子,车,后,象。车只走 直线;后 直线、斜线 都走;象 只走 斜线。
- 我们需要选择 移动方案,在这个方案中:
- 首先,对每个棋子,指定 移动方向 和 步数。(棋子也可以不移动,此时移动方向已无意义,算做一种方案)
- 然后,每秒钟,每个棋子都会同时沿着 指定的方向 前进一步,直到步数耗尽。 如果某一 整数 时刻,有棋子 重叠,或者棋子 移出了界外,则为 无效方案;否则为有效方案。
- 返回有效方案的个数。
思路:
直接按题意模拟即可。首先枚举移动方案,然后再模拟移动的过程,检查是否为有效方案。
1 | class Solution { |
Comments