2058-找出临界点之间的最小和最大距离
链表中的 临界点 定义为一个 局部极大值点 或 局部极小值点 。
如果当前节点的值 严格大于 前一个节点和后一个节点,那么这个节点就是一个 ** 局部极大值点** 。
如果当前节点的值 严格小于 前一个节点和后一个节点,那么这个节点就是一个 ** 局部极小值点** 。
注意:节点只有在同时存在前一个节点和后一个节点的情况下,才能成为一个 局部极大值点 / 极小值点 。
给你一个链表 head ,返回一个长度为 2 的数组 __[minDistance, maxDistance] ,其中
__minDistance __ 是任意两个不同临界点之间的最小距离,maxDistance
是任意两个不同临界点之间的最大距离。如果临界点少于两个,则返回 [-1,-1] 。
示例 1:
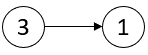
**输入:** head = [3,1]
**输出:** [-1,-1]
**解释:** 链表 [3,1] 中不存在临界点。
示例 2:

**输入:** head = [5,3,1,2,5,1,2]
**输出:** [1,3]
**解释:** 存在三个临界点:
- [5,3, _ **1**_ ,2,5,1,2]:第三个节点是一个局部极小值点,因为 1 比 3 和 2 小。
- [5,3,1,2, _ **5**_ ,1,2]:第五个节点是一个局部极大值点,因为 5 比 2 和 1 大。
- [5,3,1,2,5, _ **1**_ ,2]:第六个节点是一个局部极小值点,因为 1 比 5 和 2 小。
第五个节点和第六个节点之间距离最小。minDistance = 6 - 5 = 1 。
第三个节点和第六个节点之间距离最大。maxDistance = 6 - 3 = 3 。
示例 3:
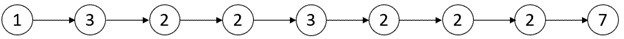
**输入:** head = [1,3,2,2,3,2,2,2,7]
**输出:** [3,3]
**解释:** 存在两个临界点:
- [1, _ **3**_ ,2,2,3,2,2,2,7]:第二个节点是一个局部极大值点,因为 3 比 1 和 2 大。
- [1,3,2,2, _ **3**_ ,2,2,2,7]:第五个节点是一个局部极大值点,因为 3 比 2 和 2 大。
最小和最大距离都存在于第二个节点和第五个节点之间。
因此,minDistance 和 maxDistance 是 5 - 2 = 3 。
注意,最后一个节点不算一个局部极大值点,因为它之后就没有节点了。
示例 4:
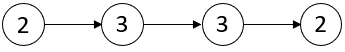
**输入:** head = [2,3,3,2]
**输出:** [-1,-1]
**解释:** 链表 [2,3,3,2] 中不存在临界点。
提示:
- 链表中节点的数量在范围
[2, 105]内 1 <= Node.val <= 105
方法一:维护上一个和第一个临界点的位置
思路与算法
我们可以对链表进行一次遍历。
当我们遍历到节点 cur 时,可以记 cur 的值、cur 后一个节点的值、cur 后两个节点的值,分别为 x, y, z。如果 y 严格大于 x 和 z,或者 y 严格小于 x 和 z,那么 cur 的后一个节点就是临界点。
由于我们需要得到任意两个临界点之间的最小距离和最大距离,而我们可以发现:
最小距离一定出现在两个相邻的临界点之间;
最大距离一定出现在第一个和最后一个临界点之间。
因此,在遍历的过程中,我们可以维护上一个临界点的位置以及第一个临界点的位置。这样一来,每当我们找到一个临界点,就可以更新最小距离和最大距离。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(n),其中 n 是给定的链表的长度。
空间复杂度:O(1)。
Comments