2069-模拟行走机器人 II

给你一个在 XY 平面上的 width x height 的网格图， 左下角 的格子为 (0, 0) ， 右上角 的格子为
(width - 1, height - 1) 。网格图中相邻格子为四个基本方向之一（"North"，"East"，"South" 和
"West"）。一个机器人初始在格子 (0, 0) ，方向为 "East" 。

机器人可以根据指令移动指定的步数。每一步，它可以执行以下操作。

沿着当前方向尝试 往前一步 。
如果机器人下一步将到达的格子 超出了边界 ，机器人会 逆时针 转 90 度，然后再尝试往前一步。

如果机器人完成了指令要求的移动步数，它将停止移动并等待下一个指令。

请你实现 Robot 类：

Robot(int width, int height) 初始化一个 width x height 的网格图，机器人初始在 (0, 0) ，方向朝 "East" 。
void step(int num) 给机器人下达前进 num 步的指令。
int[] getPos() 返回机器人当前所处的格子位置，用一个长度为 2 的数组 [x, y] 表示。
String getDir() 返回当前机器人的朝向，为 "North" ，"East" ，"South" 或者 "West" 。

示例 1：

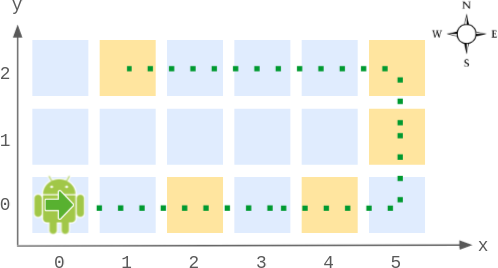
**输入：**
["Robot", "step", "step", "getPos", "getDir", "step", "step", "step", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
**输出：**
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

**解释：**
Robot robot = new Robot(6, 3); // 初始化网格图，机器人在 (0, 0) ，朝东。
robot.step(2);  // 机器人朝东移动 2 步，到达 (2, 0) ，并朝东。
robot.step(2);  // 机器人朝东移动 2 步，到达 (4, 0) ，并朝东。
robot.getPos(); // 返回 [4, 0]
robot.getDir(); // 返回 "East"
robot.step(2);  // 朝东移动 1 步到达 (5, 0) ，并朝东。
                // 下一步继续往东移动将出界，所以逆时针转变方向朝北。
                // 然后，往北移动 1 步到达 (5, 1) ，并朝北。
robot.step(1);  // 朝北移动 1 步到达 (5, 2) ，并朝 **北** （不是朝西）。
robot.step(4);  // 下一步继续往北移动将出界，所以逆时针转变方向朝西。
                // 然后，移动 4 步到 (1, 2) ，并朝西。
robot.getPos(); // 返回 [1, 2]
robot.getDir(); // 返回 "West"

提示：

2 <= width, height <= 100
1 <= num <= 105
step ，getPos 和 getDir **总共 **调用次数不超过 104 次。

方法一：模拟

思路与算法

根据题目描述，我们可以发现：机器人总是会在网格的「最外圈」进行循环移动。

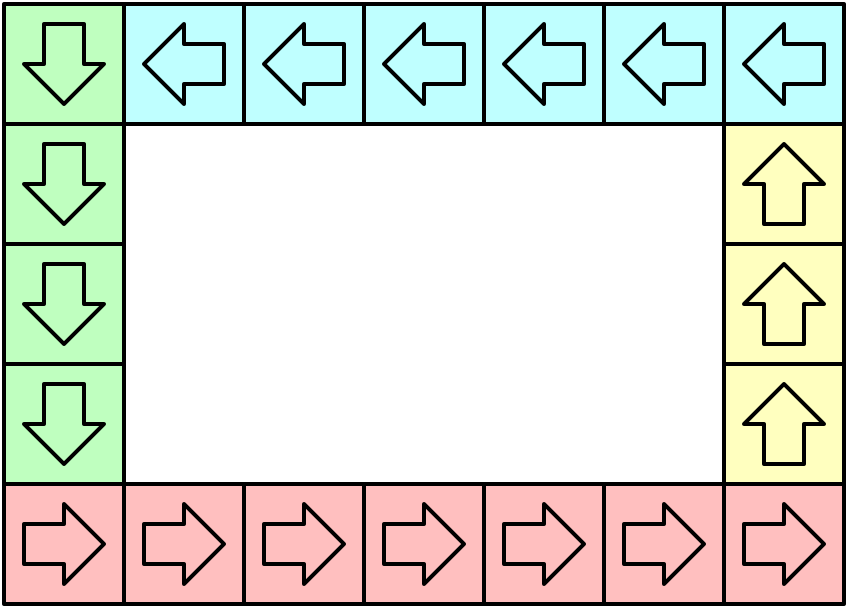{:width=”40%”}

因此，我们可以将机器人移动的循环节（位置以及移动方向）预处理出来，存储在数组中，并用一个指针 idx 指向数组中的某个位置，表示当前机器人的位置以及移动方向。

预处理可以分为四个步骤完成。如上图所示，不同颜色的网格表示机器人在对应网格上的不同方向，因此我们可以使用四个循环分别枚举每一种颜色对应的网格的位置，把它们加入预处理的数组即可。

对于题目要求实现的三个接口，我们可以依次实现：

void move(int num)：我们可以将 idx 的值增加 num。由于机器人的移动路径是循环的，我们需要将增加后的值对循环的长度取模。
int[] getPos()：我们根据 idx 返回预处理数组中的位置即可。
String getDir()：我们根据 idx 返回预处理数组中的朝向即可。

细节

需要注意的是。当机器人回到原点时，它的朝向为「南」，但机器人初始在原点时的朝向为「东」。因此我们可以将预处理数组中原点的朝向改为「南」，并使用一个布尔变量记录机器人是否移动过：

如果机器人未移动过，我们总是返回「东」朝向；
如果机器人移动过，我们根据 idx 返回预处理数组中的朝向。

代码

[sol1-C++]class Robot {
private:
    bool moved = false;
    int idx = 0;
    vector<pair<int, int>> pos;
    vector<int> dir;
    unordered_map<int, string> to_dir = {
        {0, "East"},
        {1, "North"},
        {2, "West"},
        {3, "South"}
    };
    
public:
    Robot(int width, int height) {
        for (int i = 0; i < width; ++i) {
            pos.emplace_back(i, 0);
            dir.emplace_back(0);
        }
        for (int i = 1; i < height; ++i) {
            pos.emplace_back(width - 1, i);
            dir.emplace_back(1);
        }
        for (int i = width - 2; i >= 0; --i) {
            pos.emplace_back(i, height - 1);
            dir.emplace_back(2);
        }
        for (int i = height - 2; i > 0; --i) {
            pos.emplace_back(0, i);
            dir.emplace_back(3);
        }
        dir[0] = 3;
    }
    
    void move(int num) {
        moved = true;
        idx = (idx + num) % pos.size();
    }
    
    vector<int> getPos() {
        return {pos[idx].first, pos[idx].second};
    }
    
    string getDir() {
        if (!moved) {
            return "East";
        }
        return to_dir[dir[idx]];
    }
};

[sol1-Python3]class Robot:

    TO_DIR = {
        0: "East",
        1: "North",
        2: "West",
        3: "South",
    }

    def __init__(self, width: int, height: int):
        self.moved = False
        self.idx = 0
        self.pos = list()
        self.dirs = list()

        pos_, dirs_ = self.pos, self.dirs

        for i in range(width):
            pos_.append((i, 0))
            dirs_.append(0)
        for i in range(1, height):
            pos_.append((width - 1, i))
            dirs_.append(1)
        for i in range(width - 2, -1, -1):
            pos_.append((i, height - 1))
            dirs_.append(2)
        for i in range(height - 2, 0, -1):
            pos_.append((0, i))
            dirs_.append(3)

        dirs_[0] = 3

    def move(self, num: int) -> None:
        self.moved = True
        self.idx = (self.idx + num) % len(self.pos)

    def getPos(self) -> List[int]:
        return list(self.pos[self.idx])

    def getDir(self) -> str:
        if not self.moved:
            return "East"
        return Robot.TO_DIR[self.dirs[self.idx]]

复杂度分析

时间复杂度：预处理的时间复杂度为 O(\textit{width} + \textit{height})，所有查询接口的时间复杂度均为 O(1)。
空间复杂度：O(\textit{width} + \textit{height})，即为存储预处理数组需要的空间。