2087-网格图中机器人回家的最小代价

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

给你一个 m x n 的网格图，其中 (0, 0) 是最左上角的格子，(m - 1, n - 1) 是最右下角的格子。给你一个整数数组
startPos ，startPos = [startrow, startcol] 表示 初始 有一个 机器人 在格子
(startrow, startcol) 处。同时给你一个整数数组 homePos ，homePos = [homerow, homecol]
表示机器人的 家 在格子 (homerow, homecol) 处。

机器人需要回家。每一步它可以往四个方向移动： 上 ， 下 ， 左 ， 右
，同时机器人不能移出边界。每一步移动都有一定代价。再给你两个下标从 0 开始的额整数数组：长度为 m 的数组 rowCosts
和长度为 n 的数组 colCosts 。

  • 如果机器人往 上 或者往 下 移动到第 r 行 的格子，那么代价为 rowCosts[r] 。
  • 如果机器人往 左 或者往 右 移动到第 c 列 的格子，那么代价为 colCosts[c] 。

请你返回机器人回家需要的 最小总代价 。

示例 1：

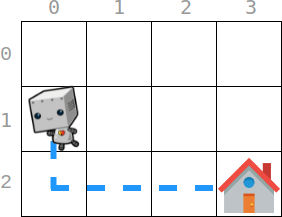
**输入：** startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
**输出：** 18
**解释：** 一个最优路径为：
从 (1, 0) 开始
-> 往下走到 ( _ **2**_ , 0) 。代价为 rowCosts[2] = 3 。
-> 往右走到 (2, _**1**_ ) 。代价为 colCosts[1] = 2 。
-> 往右走到 (2, _**2**_ ) 。代价为 colCosts[2] = 6 。
-> 往右走到 (2, _**3**_ ) 。代价为 colCosts[3] = 7 。
总代价为 3 + 2 + 6 + 7 = 18

示例 2：

**输入：** startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
**输出：** 0
**解释：** 机器人已经在家了，所以不需要移动。总代价为 0 。

提示：

  • m == rowCosts.length
  • n == colCosts.length
  • 1 <= m, n <= 105
  • 0 <= rowCosts[r], colCosts[c] <= 104
  • startPos.length == 2
  • homePos.length == 2
  • 0 <= startrow, homerow < m
  • 0 <= startcol, homecol < n

方法一：贪心

提示 1

如果在某一条路径中，相邻的两步分别为横向（左/右）和纵向（上/下）移动，那么交换这两步前后，路径的总代价不变。

提示 1 解释

由于路径的其它部分不会改变，对应部分的代价也不会改变，因此我们只需要考虑交换的两步。不妨假设在这两步的过程中，机器人从 (r, c) 移动到了 (r + 1, c + 1)。

考虑交换前后两种不同的移动方式（用 \rightarrow 表示沿着某个方向一直移动，下同）：

  • (r, c) \rightarrow (r + 1, c) \rightarrow (r + 1, c + 1)：第一步移动到 r + 1 行，代价为 rowCost}[r + 1]；第二步移动到 c + 1 列，代价为 colCost}[c + 1]。总代价为 rowCost}[r + 1] + \textit{colCost}[c + 1]。

  • (r, c) \rightarrow (r, c + 1) \rightarrow (r + 1, c + 1)：第一步移动到 c + 1 列，代价为 colCost}[c + 1]；第二步移动到 r + 1 行，代价为 rowCost}[r + 1]。总代价为 colCost}[c + 1] + \textit{rowCost}[r + 1]。

可以发现，这两种方式代价相同。因此，路径的总代价也不会改变。

提示 2

如果某一条路径中包含相反操作（即同时含有向左和向右的操作，或同时含有向上和向下的操作），那么这条路径的代价一定不优于将这些操作成对抵消后的路径。

除此之外，任意不包含任何相反操作的路径对应的总代价一定最小。

提示 2 解释

我们首先考虑前半部分。

不失一般性地，首先考虑从 (r, c) 到 (r + x, c) (x \ge 0) 的两种路径。一种路径为 (r, c) \rightarrow (r + x, c)，另一种路径为 (r, c) \rightarrow (r, c + 1) \rightarrow (r + x, c + 1) \rightarrow (r + x, c)。计算可得，后者相对于前者多出了 colCost}[c] + \textit{colCost}[c + 1] \ge 0 的总代价，亦即前者一定更优。

而对于一般的存在相反方向操作的路径，其中必定包含上述的路径片段；而将路径片段中的相反操作抵消后，新的路径在总代价上一定不高于原路径。因此，我们可以递归地抵消这些相反操作，直至路径不包含任何相反操作，同时在每次操作时，总代价一定不会增加。

综上可知，对于任意包含相反操作的路径，一定存在一个不包含相反操作的路径，后者的总代价小于等于前者。因此，最小总代价对应的路径一定是不包含相反操作的路径。

而对于所有的这些不包含任何相反操作的路径，这些路径一定是由一些（数量可能为 0）单方向的横向操作和一些（数量可能为 0）单方向的纵向操作组成。根据 提示 1，我们可以任意交换这些操作，且总代价不变。因此，任意不包含任何相反操作的路径对应的总代价一定最小。

思路与算法

根据 提示 2，我们只需要构造任意一条从起点到家的不包含相反操作的路径，该路径对应的总代价即为最小总代价。

为了方便计算，我们先让机器人向上或向下移动至家所在行，再让机器人向左或向右移动至家所在的格子，并在这过程中计算总代价。

而对于如何确定移动的方向，我们行间的上下移动为例：我们比较机器人所在行号 r_1 与家所在行号 r_2，如果 r_1 < r_2，则我们需要向下移动；如果 r_1 > r_2，则我们需要向上移动；如果 r_1 = r_2，则我们无需移动。

最终，我们返回该总代价作为答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minCost(vector<int>& startPos, vector<int>& homePos, vector<int>& rowCosts, vector<int>& colCosts) {
        int r1 = startPos[0], c1 = startPos[1];
        int r2 = homePos[0], c2 = homePos[1];
        int res = 0;   // 总代价
        // 移动至家所在行，判断行间移动方向并计算对应代价
        if (r2 >= r1){
            res += accumulate(rowCosts.begin() + r1 + 1, rowCosts.begin() + r2 + 1, 0);
        }
        else{
            res += accumulate(rowCosts.begin() + r2, rowCosts.begin() + r1, 0);
        }
        // 移动至家所在位置，判断列间移动方向并计算对应代价
        if (c2 >= c1){
            res += accumulate(colCosts.begin() + c1 + 1, colCosts.begin() + c2 + 1, 0);
        }
        else{
            res += accumulate(colCosts.begin() + c2, colCosts.begin() + c1, 0);
        }
        return res;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:
        r1, c1 = startPos[0], startPos[1]
        r2, c2 = homePos[0], homePos[1]
        res = 0   # 总代价
        # 移动至家所在行，判断行间移动方向并计算对应代价
        if r2 >= r1:
            for i in range(r1 + 1, r2 + 1):
                res += rowCosts[i]
        else:
            for i in range(r2, r1):
                res += rowCosts[i]
        # 移动至家所在位置，判断列间移动方向并计算对应代价
        if c2 >= c1:
            for i in range(c1 + 1, c2 + 1):
                res += colCosts[i]
        else:
            for i in range(c2, c1):
                res += colCosts[i]
        return res

复杂度分析

  • 时间复杂度：O(m + n)，其中 m 为网格图的行数，n 为网格图的列数。即为计算最小代价的时间复杂度。

  • 空间复杂度：O(1)。

 Comments
On this page
2087-网格图中机器人回家的最小代价