2096-从二叉树一个节点到另一个节点每一步的方向

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

给你一棵 二叉树 的根节点 root ，这棵二叉树总共有 n 个节点。每个节点的值为 1 到 n
中的一个整数，且互不相同。给你一个整数 startValue ，表示起点节点 s 的值，和另一个不同的整数 destValue ，表示终点节点
t 的值。

请找到从节点 s 到节点 t 的 最短路径 ，并以字符串的形式返回每一步的方向。每一步用 大写 字母 'L' ，'R'
和 'U' 分别表示一种方向：

  • 'L' 表示从一个节点前往它的 左孩子 节点。
  • 'R' 表示从一个节点前往它的 右孩子 节点。
  • 'U' 表示从一个节点前往它的 父 节点。

请你返回从 s 到 t 最短路径 每一步的方向。

示例 1：

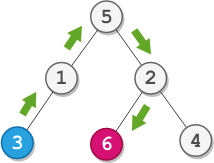
**输入：** root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
**输出：** "UURL"
**解释：** 最短路径为：3 → 1 → 5 → 2 → 6 。

示例 2：

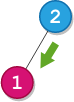
**输入：** root = [2,1], startValue = 2, destValue = 1
**输出：** "L"
**解释：** 最短路径为：2 → 1 。

提示：

  • 树中节点数目为 n 。
  • 2 <= n <= 105
  • 1 <= Node.val <= n
  • 树中所有节点的值 互不相同 。
  • 1 <= startValue, destValue <= n
  • startValue != destValue

方法一：深度优先搜索

提示 1

二叉树中一个节点到另一个节点的最短路径一定可以分为两个部分（可能为空）：从起点节点向上到两个节点的最近公共祖先，再从最近公共祖先向下到达终点节点。

注：关于「最近公共祖先」的定义，可以参见 236. 二叉树的最近公共祖先 。

提示 1 解释

首先，由于二叉树中不存在环，因此根据最近公共祖先的定义，两个节点中的路径一定经过最近公共祖先。下面我们利用反证法证明上述的路径一定最短。

我们用 a \rightarrow b 表示二叉树中 a 节点向上/向下到达 b 节点的路径，并用函数 d(a \rightarrow b) 表示该路径的长度。假设起点 s 到终点 t 的最短路径经过了最近公共祖先 l 的祖先节点（不包括本身）u，那么这条路径的长度

d(s \rightarrow l \rightarrow u \rightarrow l \rightarrow t) = d(s \rightarrow l) + d(l \rightarrow u) + d(u \rightarrow l) + d(l \rightarrow t)

与只经过最近公共祖先 l 的路径长度

d(s \rightarrow l \rightarrow t) = d(s \rightarrow l) + d(l \rightarrow t)

相比，显然有

d(s \rightarrow l \rightarrow u \rightarrow l \rightarrow t) > d(s \rightarrow l \rightarrow t).

这就产生了矛盾，因此上述命题成立。

提示 2

假设根节点向下到节点 s 的路径每一步方向组成的字符串为 path}_1，到 t 的路径对应的方向字符串为 path}_2；那么 path}_1 与 path}_2 的最长公共前缀即为根节点到 s 与 t 最近公共祖先节点的路径对应的方向字符串。

提示 2 解释

上述命题可以直接由「最近公共祖先」的定义得到。

思路与算法

根据 提示 1 与 提示 2，我们首先需要找到 s 与 t，并维护根节点到 s 与 t 的最短路径对应方向字符串 path}_1 与 path}_2。随后，我们计算两个字符串的最长公共前缀，并在 path}_1 与 path}_2 中截去这部分前缀。随后，由于 s 到最近公共祖先的路径是向上的，因此我们将处理后的 path}_1 中的所有字符均修改成代表向上的 `U’，并将处理后的 path}_2 拼接至尾部，最终得到的字符串即为待求 s 到 t 每一步的最短路径。

为了求出 path}_1 与 path}_2，一种方法是自根节点向下进行深度优先搜索，对于每个节点均更新并保存根节点到该节点的路径字符串，待找到目标节点后返回对应的字符串。但对于树为一条链的情况，这种方法的时空复杂度均为 O(n^2)，不符合题目要求。因此，我们需要尝试从 s 与 t 向上遍历直到根节点从而得到对应的路径，并反向得出目标字符串。但对于一般的二叉树数据结构，我们无法很快地得到某一个节点的父节点，因此我们需要通过深度优先搜索，利用哈希表额外维护每个节点对应的父节点。维护父节点哈希表后，我们便可以在 O(n) 的时间与空间复杂度内求出 path}_1 与 path}_2。

具体地，我们首先利用函数 dfs}(\textit{curr}) 自根节点对二叉树进行深度优先搜索，从而得到 s 与 t，以及存储每个节点父节点的哈希表 fa。随后，我们利用函数 path}(\textit{curr}) 求出根节点到 s 与 t 的路径对应字符串 path}_1 与 path}_2。在函数 path}(\textit{curr}) 中，我们维护路径字符串 res，并利用哈希表 fa 逐层向上遍历，每当求出当前节点 curr 的父节点 par 时，我们判断 curr 是 par 的左孩子还是右孩子节点，并在路径字符串的末尾添加上对应的 L' 或 R’；最终我们将 res 反转，即为待求的路径对应字符串。最后，我们计算两个路径字符串的最长公共前缀并删去，同时将 path}_1 的所有字符改为表示向上的 `U’，并与截去前缀的 path}_2 拼接作为 s 到 t 最短路径每一步的方向返回。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution {
public:
    string getDirections(TreeNode* root, int startValue, int destValue) {
        unordered_map<TreeNode*, TreeNode*> fa;   // 父节点哈希表
        TreeNode* s = nullptr;   // 起点节点
        TreeNode* t = nullptr;   // 终点节点
        
        // 深度优先搜索维护哈希表与起点终点
        function<void(TreeNode*)> dfs = [&](TreeNode* curr) {
            if (curr->val == startValue) {
                s = curr;
            }
            if (curr->val == destValue) {
                t = curr;
            }
            if (curr->left) {
                fa[curr->left] = curr;
                dfs(curr->left);
            }
            if (curr->right) {
                fa[curr->right] = curr;
                dfs(curr->right);
            }
        };
        
        dfs(root);
        
        // 求出根节点到对应节点的路径字符串
        function<string(TreeNode*)> path = [&](TreeNode* curr) {
            string res;
            while (curr != root) {
                TreeNode* par = fa[curr];
                if (curr == par->left) {
                    res.push_back('L');
                }
                else {
                    res.push_back('R');
                }
                curr = par;
            }
            reverse(res.begin(), res.end());
            return res;
        };
        
        string path1 = path(s);
        string path2 = path(t);
        // 计算最长公共前缀并删去对应部分，同时将 path_1 逐字符修改为 'U'
        int l1 = path1.size(), l2 = path2.size();
        int i = 0;
        while (i < min(l1, l2)) {
            if (path1[i] == path2[i]) {
                ++i;
            }
            else {
                break;
            }
        }
        string finalpath(l1 - i, 'U');   // 最短路径对应字符串 
        finalpath.append(path2.substr(i, l2 - i));
        return finalpath;
    }
};
class Solution:
    def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:
        fa = {}   # 父节点哈希表
        s = None   # 起点节点
        t = None   # 终点节点

        # 深度优先搜索维护哈希表与起点终点
        def dfs(curr: TreeNode) -> None:
            nonlocal s, t
            if curr.val == startValue:
                s = curr
            if curr.val == destValue:
                t = curr
            if curr.left:
                fa[curr.left] = curr
                dfs(curr.left)
            if curr.right:
                fa[curr.right] = curr
                dfs(curr.right)
        
        dfs(root)

        # 求出根节点到对应节点的路径字符串
        def path(curr: TreeNode) -> List[str]:
            res = []
            while curr != root:
                par = fa[curr]
                if curr == par.left:
                    res.append('L')
                else:
                    res.append('R')
                curr = par
            return res[::-1]
        
        path1 = path(s)
        path2 = path(t)
        # 计算最长公共前缀并删去对应部分，同时将 path_1 逐字符修改为 'U'
        l1, l2 = len(path1), len(path2)
        i = 0
        while i < min(l1, l2):
            if path1[i] == path2[i]:
                i += 1
            else:
                break
        finalpath = 'U' * (l1 - i) + ''.join(path2[i:])   # 最短路径对应字符串 
        return finalpath

**复杂度分析**

- 时间复杂度：O(n)，其中 n 为树中节点数目。深度优先搜索与维护路径的时间复杂度均为 O(n)。

- 空间复杂度：O(n)，即为深度优先搜索的栈空间开销和根节点到起点终点路径字符串的空间开销。
 Comments
On this page
2096-从二叉树一个节点到另一个节点每一步的方向