2103-环和杆

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:29 2023-09-13 16:06:29 Updated    

总计有 n 个环，环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。

给你一个长度为 2n 的字符串 rings ，表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对
，用于描述每个环：

  • 第 i 对中的 第一个 字符表示第 i 个环的 颜色 （'R'、'G'、'B'）。
  • 第 i 对中的 第二个 字符表示第 i 个环的 位置 ，也就是位于哪根杆上（'0' 到 '9'）。

例如，"R3G2B1" 表示：共有 n == 3 个环，红色的环在编号为 3 的杆上，绿色的环在编号为 2 的杆上，蓝色的环在编号为 1 的杆上。

找出所有集齐 全部三种颜色 环的杆，并返回这种杆的数量。

示例 1：

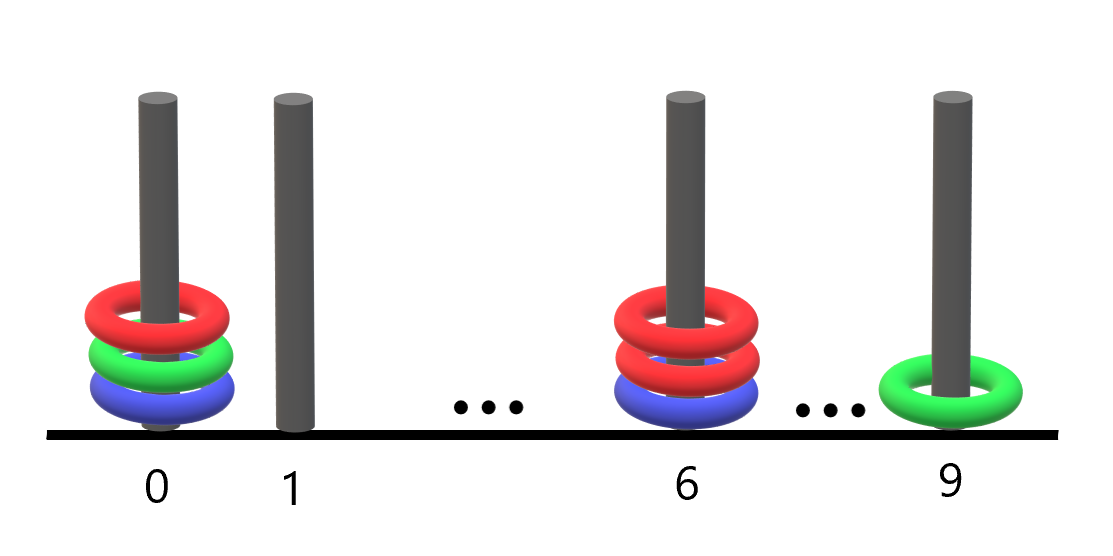
**输入：** rings = "B0B6G0R6R0R6G9"
**输出：** 1
**解释：**
- 编号 0 的杆上有 3 个环，集齐全部颜色：红、绿、蓝。
- 编号 6 的杆上有 3 个环，但只有红、蓝两种颜色。
- 编号 9 的杆上只有 1 个绿色环。
因此，集齐全部三种颜色环的杆的数目为 1 。

示例 2：

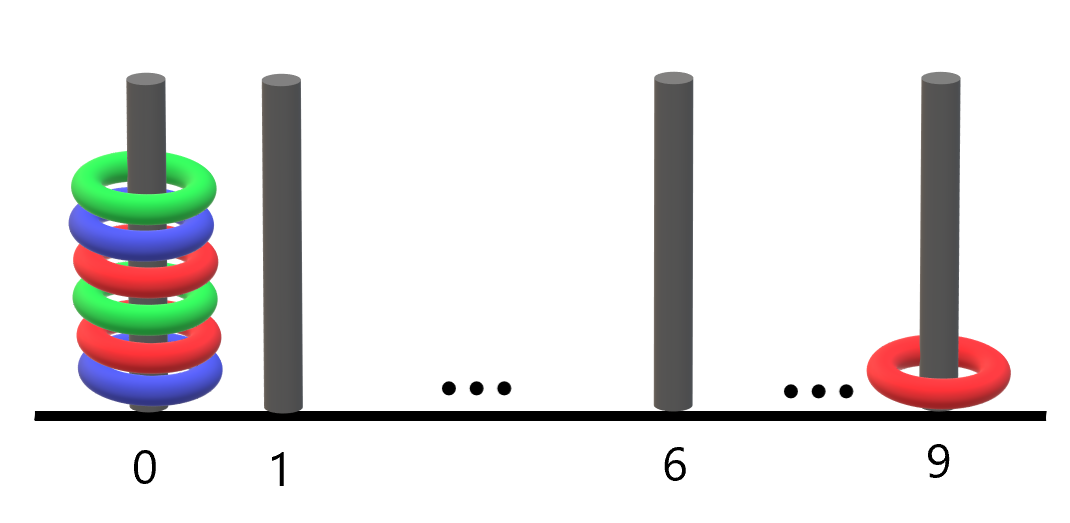
**输入：** rings = "B0R0G0R9R0B0G0"
**输出：** 1
**解释：**
- 编号 0 的杆上有 6 个环，集齐全部颜色：红、绿、蓝。
- 编号 9 的杆上只有 1 个红色环。
因此，集齐全部三种颜色环的杆的数目为 1 。

示例 3：

**输入：** rings = "G4"
**输出：** 0
**解释：**
只给了一个环，因此，不存在集齐全部三种颜色环的杆。

提示：

  • rings.length == 2 * n
  • 1 <= n <= 100
  • 如 i 是 偶数 ，则 rings[i] 的值可以取 'R'、'G' 或 'B'（下标从 0 开始计数）
  • 如 i 是 奇数 ，则 rings[i] 的值可以取 '0' 到 '9' 中的一个数字（下标从 0 开始计数）

方法一：维护每根杆的状态

思路与算法

我们可以遍历字符串的每个颜色位置对，来模拟套环的过程。

对于每一个环，由于我们只关心它上面有哪些颜色的环，而不在意具体的数量；同时是否有某一种颜色的环的状态相互独立，因此我们可以用一个 3 二进制位的整数来表示每个环的状态。具体地，从低到高第一位表示是否有红色的环，第二位表示是否有蓝色的环，第三位表示是否有绿色的环；每一位为 1 则代表当前杆上有对应颜色的环，为 0 则代表没有。当套上某种颜色的环后，无论该二进制位之前取值如何，新的取值一定为 1，这等价于对应二进制位对 1 取或的操作。

我们可以用一个长度为 10 的状态数组来表示每个环的状态，数组下标即为杆的编号。在模拟开始前，所有环的状态对应的整数均为 0。在遍历到每个颜色位置对时，我们首先看第二个字符寻找出对应的下标，同时根据环的颜色对状态值的对应二进制位对 1 取或。当遍历完成后，我们遍历状态数组，统计状态值为 (111)_2 = 7 （代表对应杆上有三种颜色的环）的个数，并返回该个数作为答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int countPoints(string rings) {
        int n = rings.size();
        vector<int> status(10);   // 状态数组
        // 遍历颜色位置对维护状态数组
        for (int i = 0; i < n; i += 2) {
            int idx = rings[i+1] - '0';
            if (rings[i] == 'R') {
                status[idx] |= 1;
            }
            else if (rings[i] == 'G') {
                status[idx] |= 2;
            }
            else {
                status[idx] |= 4;
            }
        }
        // 统计集齐三色环的杆的数量
        int res = 0;
        for (int i = 0; i < 10; ++i) {
            if (status[i] == 7) {
                ++res;
            }
        }
        return res;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def countPoints(self, rings: str) -> int:
        n = len(rings)
        status = [0] * 10   # 状态数组
        # 遍历颜色位置对维护状态数组
        for i in range(0, n, 2):
            idx = int(rings[i+1])
            if rings[i] == 'R':
                status[idx] |= 1
            elif rings[i] == 'G':
                status[idx] |= 2
            else:
                status[idx] |= 4
        # 统计集齐三色环的杆的数量
        res = 0
        for i in range(10):
            if status[i] == 7:
                res += 1
        return res

复杂度分析

  • 时间复杂度：O(n + k)，其中 n 为 rings 的长度，k 为杆的数量。初始化杆状态数组与统计数量的时间复杂度为 O(k)，遍历字符串的时间复杂度为 O(n)。

  • 空间复杂度：O(k)，即为状态数组的空间开销。

 Comments
On this page
2103-环和杆