2116-判断一个括号字符串是否有效
一个括号字符串是只由 '(' 和 ')' 组成的 非空 字符串。如果一个字符串满足下面 任意 一个条件,那么它就是有效的:
- 字符串为
(). - 它可以表示为
AB(A与B连接),其中A和B都是有效括号字符串。 - 它可以表示为
(A),其中A是一个有效括号字符串。
给你一个括号字符串 s 和一个字符串 locked ,两者长度都为 n 。locked 是一个二进制字符串,只包含 '0' 和'1' 。对于 locked 中 每一个 下标 i :
- 如果
locked[i]是'1',你 不能 改变s[i]。 - 如果
locked[i]是'0',你 可以 将s[i]变为'('或者')'。
如果你可以将 s 变为有效括号字符串,请你返回 true ,否则返回 false 。
示例 1:
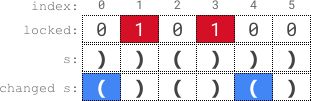
**输入:** s = "))()))", locked = "010100"
**输出:** true
**解释:** locked[1] == '1' 和 locked[3] == '1' ,所以我们无法改变 s[1] 或者 s[3] 。
我们可以将 s[0] 和 s[4] 变为 '(' ,不改变 s[2] 和 s[5] ,使 s 变为有效字符串。
示例 2:
**输入:** s = "()()", locked = "0000"
**输出:** true
**解释:** 我们不需要做任何改变,因为 s 已经是有效字符串了。
示例 3:
**输入:** s = ")", locked = "0"
**输出:** false
**解释:** locked 允许改变 s[0] 。
但无论将 s[0] 变为 '(' 或者 ')' 都无法使 s 变为有效字符串。
提示:
n == s.length == locked.length1 <= n <= 105s[i]要么是'('要么是')'。locked[i]要么是'0'要么是'1'。
方法一:数学
思路与算法
我们可以如下定义并计算一个括号字符串的「分数」:
考虑一个初值为 0 的整数,遍历该字符串,如果遇到左括号,则将该整数加上 1,如果遇到右括号,则将该整数减去 1。最终得到的数值即为括号字符串的分数。
那么,根据有效括号字符串的定义,我们可以利用「分数」的概念给出该定义的等价条件:
该字符串的分数为 0,且该字符串任意前缀的分数均大于等于 0。
读者可以自行尝试证明上述两个条件的等价性。
我们同样可以用「分数」的概念判断一个部分可变的括号字符串 s 能否变为有效字符串。
为叙述方便,我们首先给出「有效前缀」的定义:
如果括号字符串的某个前缀字符串满足它本身及它的所有前缀的分数均大于等于 0,则称该前缀为有效前缀。
可以看出,一个有效括号字符串的任意前缀均为「有效前缀」。
我们可以对字符串 s,定义对应的最大分数数组 mx 和最小有效分数数组 mn。具体地:
mx}[i + 1] 代表前缀 s[0..i] 可以达到的最大分数;
mn}[i + 1] 为前缀 s[0..i] 可以达到的最小分数及作为有效前缀所需的最小分数两者的较大值。
其中「作为有效前缀所需的最小分数」的取值,由于字符串分数的奇偶性一定与字符串长度的奇偶性相同,因此取值会有以下两种情况:
i 为偶数,此时最小分数为 0;
i 为奇数,此时最小分数为 1。
用公式表达,即为 (i + 1) \bmod 2。
对于 i = 0 的情况,有 mx}[0] = \textit{mn}[0] = 0。
我们从左至右遍历字符串 s,并相应维护 mx 和 mn 数组。具体地,当遍历到下标 i 时,根据 locked}[i] 的不同取值,会有以下两种情况:
locked}[i] = 1,此时 s[i] 的取值无法更改。因此 mx}[i + 1] = \textit{mx}[i] + \textit{diff,其中 diff 为 s[i] 的分数。同理,mn}[i + 1] = \max(\textit{mn}[i] + \textit{diff}, (i + 1) \bmod 2)。
locked}[i] = 0,此时 s[i] 的取值可以更改。因此 mx}[i + 1] = \textit{mx}[i] + 1,且 mn}[i + 1] = \max(\textit{mn}[i] - 1, (i + 1) \bmod 2)。
在遍历的过程中,如果对于某一下标 i,有 mx}[i] < \textit{mn}[i],那么 s[0..i] 无法通过变换成为有效前缀,也就是说 s 无法通过变换成为有效字符串,此时直接返回 false。
当遍历完成后,我们只需要确定 s 是否可以通过变换使得分数为 0 即可。假设 s 的长度为 n,这等价于判断 mn}[n] 是否为 0。如果 mn}[n] = 0,则 s 可以通过变换成为有效括号字符串,我们应返回 true;反之则不能,应返回 false。
细节
由上述的推导过程,我们容易发现,在计算 mx}[i + 1] 与 mn}[i + 1] 时,我们并不需要用到整个 mx 和 mn 数组,只需要 mx}[i] 与 mn}[i] 的取值。因此,我们可以用两个同名整数来替代 mx 和 mn 数组。具体转移如下:
mx 和 mn 的初值为 0;
locked}[i] = 1 时,有 mx} = \textit{mx} + \textit{diff,mn} = \max(\textit{mn} + \textit{diff}, (i + 1) \bmod 2);
locked}[i] = 0 时,有 mx} = \textit{mx} + 1,mn} = \max(\textit{mn} - 1, (i + 1) \bmod 2);
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(n),其中 n 为 s 的长度。即为遍历字符串维护 mx 和 mn 并判断 s 能否变为有效字符串的时间复杂度。
空间复杂度:O(1)。