2127-参加会议的最多员工数
一个公司准备组织一场会议,邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子,可以坐下 任意数目 的员工。
员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工,每位员工 当且仅当
他被安排在喜欢员工的旁边,他才会参加会议。每位员工喜欢的员工 不会 是他自己。
给你一个下标从 0 开始的整数数组 favorite ,其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的
最多员工数目 。
示例 1:
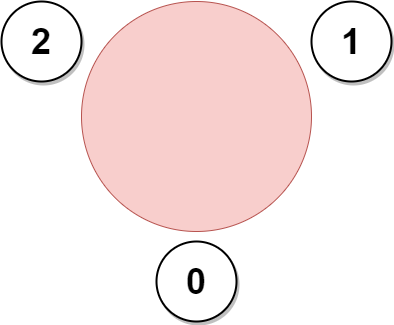
**输入:** favorite = [2,2,1,2]
**输出:** 3
**解释:**
上图展示了公司邀请员工 0,1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议,因为员工 2 没办法同时坐在 0,1 和 3 员工的旁边。
注意,公司也可以邀请员工 1,2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。
示例 2:
**输入:** favorite = [1,2,0]
**输出:** 3
**解释:**
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示:
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。
示例 3:
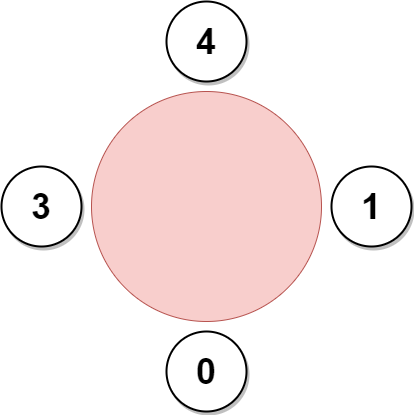
**输入:** favorite = [3,0,1,4,1]
**输出:** 4
**解释:**
上图展示了公司可以邀请员工 0,1,3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加,因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。
提示:
n == favorite.length2 <= n <= 1050 <= favorite[i] <= n - 1favorite[i] != i
方法一:分类讨论 + 拓扑排序
提示 1
如果我们把每个员工看成图上的一个节点,如果员工 x 喜欢员工 y,就在从 x 对应的节点到 y 对应的节点连一条边,那么形成的图是什么结构的?
提示 1 解释
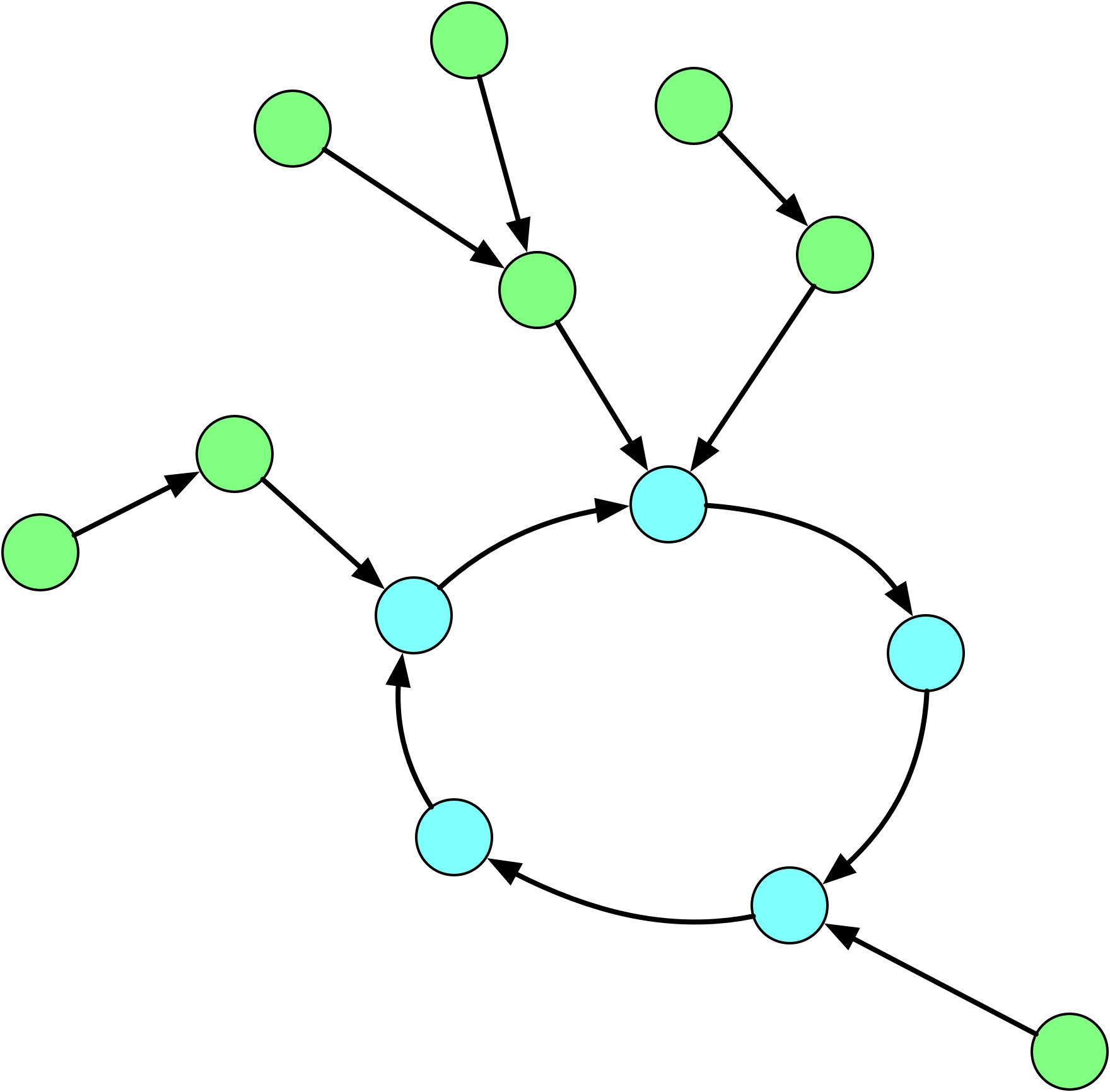
形成的图会由若干颗「基环内向树」组成。所谓「基环内向树」,就是形如下图所示的结构:
 {:width=”40%”}
{:width=”40%”}
原因如下:
我们从任意一个节点 x 开始在图上进行「游走」,由于每个员工只有一位喜欢的员工,因此每个节点在图上只会有一条出边,即「游走」的过程是唯一的。由于图上有 n 个节点,因此在 n+1 步以内,一定会走到一个重复的节点,那么在第一次经过该节点之后,到第二次经过该节点之前的所有节点,以及该节点本身,就组成了一个环,如上图的蓝色节点所示。
对于不在环上的节点,我们已经说明了从它们开始「游走」也一定会进入到环中。在到达环上的节点之前,它们不会重复经过节点(否则就有两个环了,我们可以证明一个连通分量中是不可能有两个环的:因为每个节点只有一条出边,因此如果有两个环并且它们连通,那么必然某个环上有一个点有两条出边,一条出边指向同一个环上的节点,另一条出边可以使得它到达另一个环,这就产生了矛盾),那么它们就形成了类似树的结构,如上图的绿色节点所示。
需要注意的是,一个单独的环也是「基环内向树」,它是一种特殊情况,即没有绿色的节点。
思路与算法
既然我们知道了图由若干颗「基环内向树」组成,那么我们就可以想一想,每一颗「基环内向树」的哪一部分可以被安排参加会议。
我们首先讨论特殊的情况,即一个单独的环(或若干个环),并且所有环的大小都 \geq 3。可以发现,我们按照环上的顺序给对应的员工安排座位是满足要求的,因为对于每一个环上的员工,它喜欢的员工就在它的旁边。并且,我们必须安排环上的所有员工,因为如果有缺失,那么喜欢那位缺失了的员工的员工就无法满足要求了。
但如果我们已经安排了某一个环上的所有员工,剩余的环就没有办法安排了。这是因为已经安排的那个环是没有办法被「断开」的:断开的本质就是相邻位置员工的缺失。因此,我们可以得出一个重要的结论:
如果我们想安排大小 \geq 3 的环,我们最多只能安排一个,并且环需要是完整的。
那么如果是环大小 \geq 3 的「基环内向树」呢?如果我们安排了不在环上的节点,那么从该节点开始,我们需要不断安排当前节点喜欢的员工,这实际上就是「游走」的过程。而当我们游走到环上并到达环上最后一个未经过的节点时,该节点的下一个节点(即喜欢的员工)已经被安排过,所以最后一个未经过的节点就无法被安排,不满足要求。因此,我们不能安排任何不在环上的节点,只能安排在环上的节点,就得出了另一个的结论:
所有环大小 \geq 3 的「基环内向树」与一个大小相同(指环的部分)的环是等价的。
那么最后我们只需要考虑大小 =2 的环或者「基环内向树」了。这里的特殊之处在于,大小 =2 的环可以安排多个:因为环上的两个点是互相喜欢的,因此只需要它们相邻即可,而没有其它的要求。而对于环大小 =2 的「基环内向树」,如果我们安排了不在环上的节点,那么游走完环上两个节点之后,同样是满足要求的,并且我们甚至可以继续延伸(反向「游走」),到另一个不在环上的节点为止。如下图所示,包含 X 的节点就是可以安排参加会议的节点。
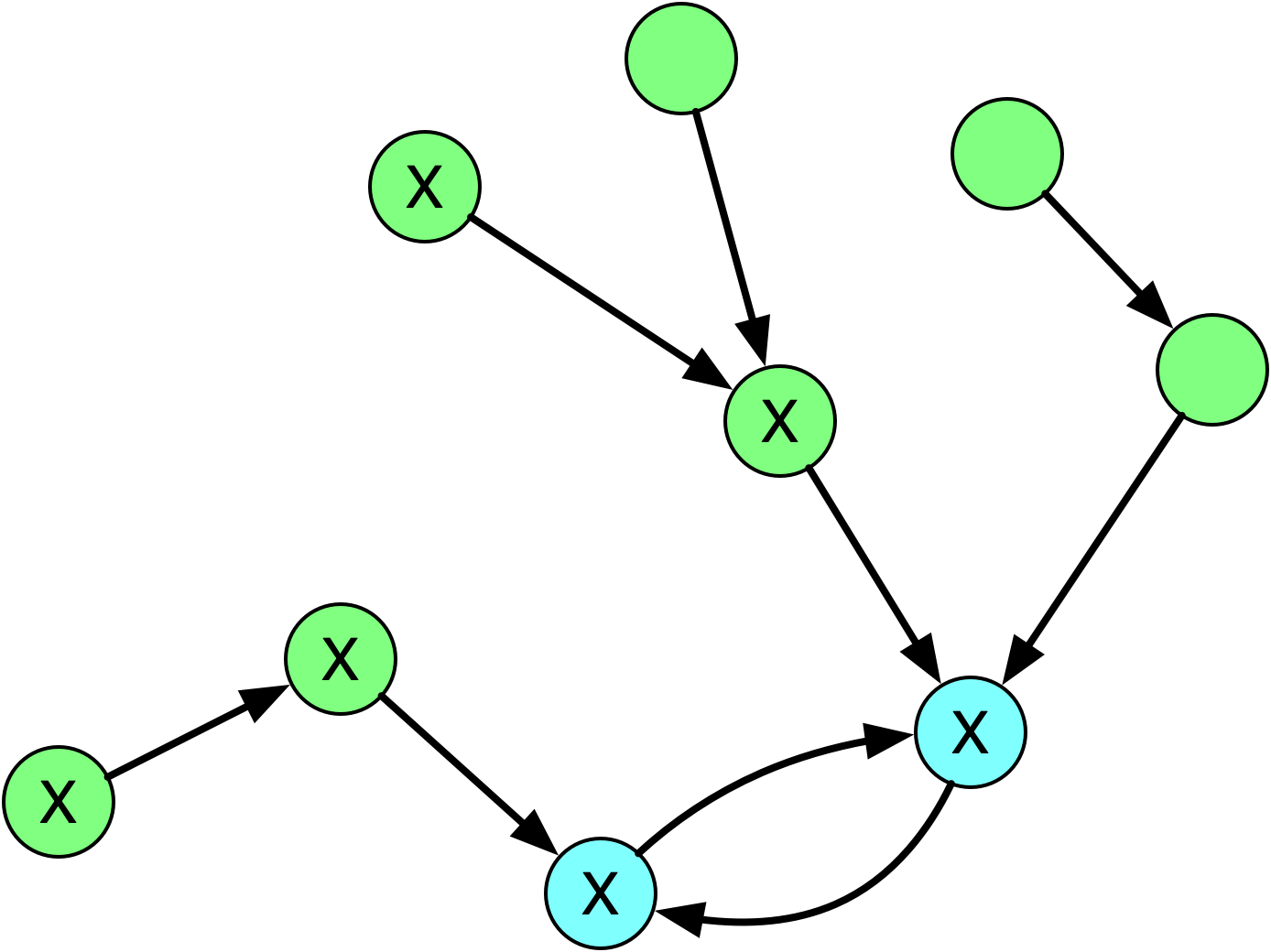 {:width=”40%”}
{:width=”40%”}
并且同样地,对于每一棵环大小 =2 的「基环内向树」,我们都可以取出这样一条「双向游走」路径进行安排,它们之间不会影响。综上所述,原问题的答案即为下面二者中的最大值:
最大的环的大小;
所有环大小 =2 的「基环内向树」上的最长的「双向游走」路径之和。
为了求解「基环内向树」上的最长的「双向游走」路径,我们可以使用拓扑排序 + 动态规划的方法。记 f[i] 表示到节点 i 为止的最长「游走」路径经过的节点个数,那么状态方程即为:
f[i] = \max_{j \to i}{ f[j] } + 1
即我们考虑节点 i 的上一个节点 j,在图中必须有从 j 到 i 的一条有向边,这样我们就可以从 j 转移到 i。如果不存在满足要求的 j(例如「基环内向树」退化成一个大小 =2 的环),那么 f[i] = 1。状态转移可以和拓扑排序同时进行。
在拓扑排序完成后,剩余没有被弹出过队列的节点就是环上的节点。我们可以找出每一个环。如果环的大小 \geq 3,我们就用其来更新最大的环的大小;如果环的大小 =2,设环上的两个节点为 x 和 y,那么该「基环内向树」上最长的「双向游走」的路径长度就是 f[x] + f[y]。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(n)。图中有 n 个节点和 n 条边,拓扑排序需要的时间为 O(n),后续找出所有环的时间也为 O(n)。
空间复杂度:O(n)。我们需要若干个长度为 n 的数组。