2133-检查是否每一行每一列都包含全部整数

对一个大小为 n x n 的矩阵而言，如果其每一行和每一列都包含从 1 到 n 的 全部 整数（含 1 和
n），则认为该矩阵是一个 有效 矩阵。

给你一个大小为 n x n 的整数矩阵 matrix ，请你判断矩阵是否为一个有效矩阵：如果是，返回 true ；否则，返回 false 。

示例 1：

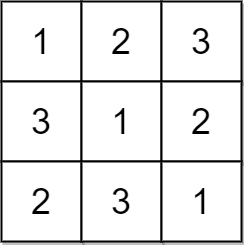
**输入：** matrix = [[1,2,3],[3,1,2],[2,3,1]]
**输出：** true
**解释：** 在此例中，n = 3 ，每一行和每一列都包含数字 1、2、3 。
因此，返回 true 。

示例 2：

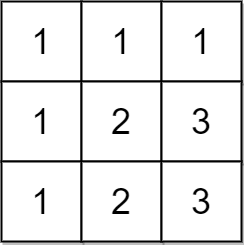
**输入：** matrix = [[1,1,1],[1,2,3],[1,2,3]]
**输出：** false
**解释：** 在此例中，n = 3 ，但第一行和第一列不包含数字 2 和 3 。
因此，返回 false 。

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• 1 <= matrix[i][j] <= n

方法一：哈希表

思路与算法

由于矩阵元素仅由从 1 到 n 的整数构成，因此，「某一行/列包含从 1 到 n 的所有整数」等价于「某一行/列的数值互不重复」。

因此，在遍历每一行/列的过程中，我们可以用一个哈希集合 occur 维护该行/列出现过的整数。如果遍历到某一个在 occur 中存在的整数，则说明该行/列没有包含从 1 到 n 的所有整数，此时我们返回 false。

当遍历完成全部行与列后，每一行/列都包含从 1 到 n 的所有整数，则说明该矩阵为有效矩阵，此时我们返回 true。

代码

[sol1-C++]

class Solution {
public:
    bool checkValid(vector<vector<int>>& matrix) {
        int n = matrix.size();
        unordered_set<int> occur;   // 每一行/列出现过的整数
        // 判断每一行是否符合要求
        for (int i = 0; i < n; ++i) {
            occur.clear();   // 确保统计前哈希表为空
            for (int j = 0; j < n; ++j) {
                if (occur.count(matrix[i][j])) {
                    // 出现重复整数，该行不符合要求
                    return false;
                }
                occur.insert(matrix[i][j]);
            }
        }
        // 判断每一列是否符合要求
        for (int i = 0; i < n; ++i) {
            occur.clear();   // 确保统计前哈希表为空
            for (int j = 0; j < n; ++j) {
                if (occur.count(matrix[j][i])) {
                    // 出现重复整数，该列不符合要求
                    return false;
                }
                occur.insert(matrix[j][i]);
            }
        }
        return true;
    }
};

[sol1-Python3]

class Solution:
    def checkValid(self, matrix: List[List[int]]) -> bool:
        n = len(matrix)
        occur = set()   # 每一行/列出现过的整数
        # 判断每一行是否符合要求
        for i in range(n):
            occur.clear()   # 确保统计前哈希表为空
            for j in range(n):
                if matrix[i][j] in occur:
                    # 出现重复整数，该行不符合要求
                    return False
                occur.add(matrix[i][j])
        # 判断每一列是否符合要求
        for i in range(n):
            occur.clear()   # 确保统计前哈希表为空
            for j in range(n):
                if matrix[j][i] in occur:
                    # 出现重复整数，该列不符合要求
                    return False
                occur.add(matrix[j][i])
        return True

复杂度分析

• 时间复杂度：O(n^2)，其中 n 为矩阵 matrix 的长或宽。判断每一行或列是否符合要求的时间复杂度为 O(n)，我们共需判断 O(n) 次。

• 空间复杂度：O(n)，即为哈希表的空间开销。