2136-全部开花的最早一天

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

你有 n 枚花的种子。每枚种子必须先种下，才能开始生长、开花。播种需要时间，种子的生长也是如此。给你两个下标从 0 开始的整数数组
plantTime 和 growTime ，每个数组的长度都是 n ：

  • plantTime[i] 是 播种 第 i 枚种子所需的 完整天数 。每天，你只能为播种某一枚种子而劳作。 无须 连续几天都在种同一枚种子，但是种子播种必须在你工作的天数达到 plantTime[i] 之后才算完成。
  • growTime[i] 是第 i 枚种子完全种下后生长所需的 完整天数 。在它生长的最后一天 之后 ，将会开花并且永远 绽放 。

从第 0 开始，你可以按 任意 顺序播种种子。

返回所有种子都开花的 最早 一天是第几天。

示例 1：

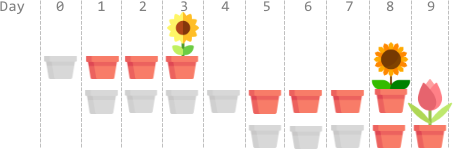
**输入：** plantTime = [1,4,3], growTime = [2,3,1]
**输出：** 9
**解释：** 灰色的花盆表示播种的日子，彩色的花盆表示生长的日子，花朵表示开花的日子。
一种最优方案是：
第 0 天，播种第 0 枚种子，种子生长 2 整天。并在第 3 天开花。
第 1、2、3、4 天，播种第 1 枚种子。种子生长 3 整天，并在第 8 天开花。
第 5、6、7 天，播种第 2 枚种子。种子生长 1 整天，并在第 9 天开花。
因此，在第 9 天，所有种子都开花。

示例 2：

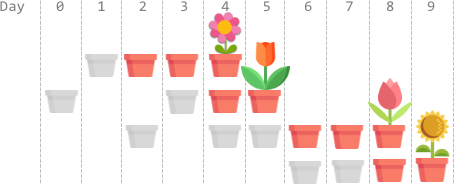
**输入：** plantTime = [1,2,3,2], growTime = [2,1,2,1]
**输出：** 9
**解释：** 灰色的花盆表示播种的日子，彩色的花盆表示生长的日子，花朵表示开花的日子。 
一种最优方案是：
第 1 天，播种第 0 枚种子，种子生长 2 整天。并在第 4 天开花。
第 0、3 天，播种第 1 枚种子。种子生长 1 整天，并在第 5 天开花。
第 2、4、5 天，播种第 2 枚种子。种子生长 2 整天，并在第 8 天开花。
第 6、7 天，播种第 3 枚种子。种子生长 1 整天，并在第 9 天开花。
因此，在第 9 天，所有种子都开花。

示例 3：

**输入：** plantTime = [1], growTime = [1]
**输出：** 2
**解释：** 第 0 天，播种第 0 枚种子。种子需要生长 1 整天，然后在第 2 天开花。
因此，在第 2 天，所有种子都开花。

提示：

  • n == plantTime.length == growTime.length
  • 1 <= n <= 105
  • 1 <= plantTime[i], growTime[i] <= 104

方法一：自定义排序

思路与算法

为了便于叙述，我们将数组 plantTime 和 growTime 简写为 p 和 g。

首先我们可以发现，一定存在一种播种方法，是每次完整播种完一颗种子再接着播种下一颗的。

我们可以使用交换法。假设有两颗种子 i 和 j，种子 i 后播种完成，但在播种种子 i 的过程中穿插播种了 x 次种子 j。那么我们可以把种子 i 播种的 p_i 次和种子 j 在其中播种的 x 次放在一起升序排序，将最小的 x 天重新分配给种子 j，剩余最大的 p_i 天分配给种子 i。

这样一来，种子 j 播种的时间整体提前了，因此其播种结束的时间也会提前或不变。而种子 i 播种结束的时间不变。我们不断地挑选 i 和 j，直到找不到满足要求的 i 和 j 为止。此时，我们就得到了满足上述要求的一种播种方法，并且在交换的过程中，答案没有变差。

因此，本题本质上是要给出 0, 1, \cdots, n - 1 的一个排列，并按照这个排列的顺序依次播种每一颗种子。当我们播种第 i 颗种子时，如果统计出前面所有种子的播种时间之和 prev，加上第 i 颗种子的播种时间 p_i 和生长时间 g_i，即为开花时间。所有开花时间中的最大值即为答案。

排序方法

那么我们应该按照什么方法进行排序呢？我们可以从一个简单的例子入手：假设在某一个排列中，种子 i 和 j 在相邻位置，并且第 i 颗种子先播种。假设第 i 颗种子之前的所有种子的播种总时间为 prev，那么第 i 颗种子开花的时间为：

\textit{prev} + p_i + g_i

第 j 颗种子开花的时间为：

\textit{prev} + p_i + p_j + g_j

我们知道，排序可以看成若干次相邻元素交换操作的和（例如经典的冒泡排序，每次只会交换相邻元素）。那么如果我们希望交换 i 和 j，一定是因为交换后答案更优。而答案是由所有种子开花时间的最大值决定的，交换 i 和 j 并不会改变其它种子的开花时间，那么我们只需要考虑第 i 颗和第 j 颗种子开花时间的较大值。因此如果：

\max{ \textit{prev} + p_i + g_i, \textit{prev} + p_i + p_j + g_j } > \max{ \textit{prev} + p_j + g_j, \textit{prev} + p_j + p_i + g_i }

那么我们就可以交换 i 和 j。

上述不等式可以简化为：

p_i + \max{ g_i, p_j + g_j } > p_j + \max{ g_j, p_i + g_i } \tag{1}

这样就只和 i, j 有关而与前面的播种总时间无关。它还可以继续进行优化，我们可以考虑 g_i 和 g_j 的大小关系：

  • 如果 g_i > g_j，那么 (1) 式可以简化为：

    \begin{aligned}
    & p_i + \max{ g_i, p_j + g_j } > p_i + p_j + g_i \
    \Leftrightarrow \quad & \max{ g_i, p_j + g_j } > p_j + g_i
    \end{aligned}

    如果 (1) 式成立，那么要么 g_i > p_j + g_i，要么 p_j + g_j > p_j + g_i。然而前者显然不满足，后者满足当且仅当 g_j > g_i，与假设 g_i > g_j 矛盾。因此 (1) 式一定不成立。同样我们可以证明将 (1) 式的大于号改成等号也不可能成立，因此一定有：

    p_i + \max{ g_i, p_j + g_j } < p_j + \max{ g_j, p_i + g_i }

  • 如果 g_i < g_j，那么 (1) 式可以简化为：

    \begin{aligned}
    & p_i + p_j + g_j > p_j + \max{ g_j, p_i + g_i } \
    \Leftrightarrow \quad & p_i + g_j > \max{ g_j, p_i + g_i }
    \end{aligned}

    由于 p_i + g_j > g_j 以及 p_i + g_j > p_i + g_i 均成立，因此 (1) 式一定成立。

  • 如果 g_i = g_j，那么 (1) 式可以简化为：

    p_i + p_j + g_j > p_j + p_i + g_i

    其一定不成立，但如果改成等号就一定成立。

综上所述，g_i > g_j, g_i = g_j, g_i < g_j 分别对应着 (1) 式取小于号、等号、大于号。因此 (1) 式可以直接简化为：

g_i < g_j \tag{2}

也就是说，如果 g_i < g_j，那么我们交换 i 和 j 是可能使得答案变优的。由于 g 满足全序关系（因为只有一个变量，任意两个 g 元素都是可以进行比较），因此我们直接按照 g 进行降序排序，就可以得到一个最优的排列。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
        int n = plantTime.size();
        vector<int> id(n);  
        iota(id.begin(), id.end(), 0);
        sort(id.begin(), id.end(), [&](int i, int j) {
            return growTime[i] > growTime[j];
        });
        int prev = 0, ans = 0;
        for (int i: id) {
            ans = max(ans, prev + plantTime[i] + growTime[i]);
            prev += plantTime[i];
        }
        return ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def earliestFullBloom(self, plantTime: List[int], growTime: List[int]) -> int:
        def compare_fn(i: int, j: int) -> int:
            if growTime[i] > growTime[j]:
                return -1
            if growTime[i] < growTime[j]:
                return 1
            return 0
        
        n = len(plantTime)
        idx = list(range(n))
        idx.sort(key=cmp_to_key(compare_fn))
        
        prev = ans = 0
        for i in idx:
            ans = max(ans, prev + plantTime[i] + growTime[i])
            prev += plantTime[i]
        return ans

复杂度分析

  • 时间复杂度：O(n \log n)。

  • 空间复杂度：O(n)。

 Comments
On this page
2136-全部开花的最早一天