2141-同时运行 N 台电脑的最长时间

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:28 2023-09-13 16:06:28 Updated    

你有 n 台电脑。给你整数 n 和一个下标从 0 开始的整数数组 batteries ，其中第 i 个电池可以让一台电脑 **运行
**batteries[i] 分钟。你想使用这些电池让 全部 n 台电脑 同时 运行。

一开始，你可以给每台电脑连接 至多一个电池 。然后在任意整数时刻，你都可以将一台电脑与它的电池断开连接，并连接另一个电池，你可以进行这个操作
任意次 。新连接的电池可以是一个全新的电池，也可以是别的电脑用过的电池。断开连接和连接新的电池不会花费任何时间。

注意，你不能给电池充电。

请你返回你可以让 n 台电脑同时运行的 最长 分钟数。

示例 1：

**输入：** n = 2, batteries = [3,3,3]
**输出：** 4
**解释：**
一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 1 连接。
2 分钟后，将第二台电脑与电池 1 断开连接，并连接电池 2 。注意，电池 0 还可以供电 1 分钟。
在第 3 分钟结尾，你需要将第一台电脑与电池 0 断开连接，然后连接电池 1 。
在第 4 分钟结尾，电池 1 也被耗尽，第一台电脑无法继续运行。
我们最多能同时让两台电脑同时运行 4 分钟，所以我们返回 4 。

示例 2：

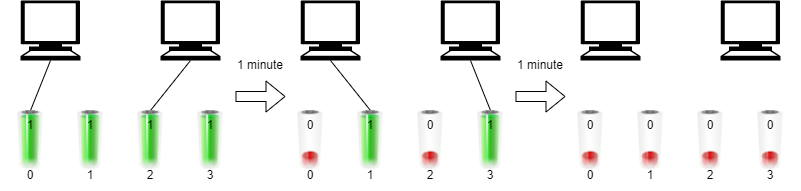
**输入：** n = 2, batteries = [1,1,1,1]
**输出：** 2
**解释：**
一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 2 连接。
一分钟后，电池 0 和电池 2 同时耗尽，所以你需要将它们断开连接，并将电池 1 和第一台电脑连接，电池 3 和第二台电脑连接。
1 分钟后，电池 1 和电池 3 也耗尽了，所以两台电脑都无法继续运行。
我们最多能让两台电脑同时运行 2 分钟，所以我们返回 2 。

提示：

  • 1 <= n <= batteries.length <= 105
  • 1 <= batteries[i] <= 109

方法一：二分查找

思路与算法

假设最多可以运行 k 分钟，那么我们就可以画一个 k 行 n 列的表 A，其中位置 (i, j) 需要填写一个在 [0, m) 范围内的数（这里 m 表示数组 batteries 的长度），表示第 j 台电脑在第 i 分钟使用了电池 A(i, j)。

根据题目的要求，这个表有如下的限制：

  • 同一行的元素必须互不相同。即在某一分钟内，所有的 n 台电脑使用的电池都不相同；

  • 每一个在 [0, m) 范围内的数 x 的出现次数都不能超过对应的 batteries}[x]。

同时，第一个限制间接地要求了 x 的出现次数不能超过 k。也就是说，x 的出现次数不能超过：

\min(\textit{batteries}[x], k)

k 是可以通过二分查找确定的。因为如果可以运行 k 分钟，那么也一定可以运行 k-1, k-2, \cdots 分钟。因此一定存在一个 k’，使得我们可以运行 \leq k’ 分钟，但不能运行 > k’ 分钟，此时 k’ 就是我们需要求出的答案。

在二分查找的每一步中，设当前需要进行判定的分钟数为 mid，那么每一个 x 的出现次数不能超过 occ}(x) = \min(\textit{batteries}[x], \textit{mid})。如果所有 occ}(x) 的和没有超过 mid} \times n，那么我们甚至都找不到 mid} \times n 个数来填表，因此一定没有办法满足要求；而如果所有 occ}(x) 的和大于等于 mid} \times n，那么我们可以断定，一定是可以根据限制来填表的。

这是因为我们只要按照列优先的顺序，将这些数按照从小到达的顺序填入表中即可，其中数 x 连续地填写 occ}(x) 次。显然第二个限制一定是满足要求的，因为 occ}(x) \leq \textit{batteries}[x]。而第一个限制同样是满足要求的，因为 occ}(x) \leq \textit{mid，并且我们是按照列优先的顺序连续填写 x 的，而一共有 mid 行，因此不会有某一行出现超过一个 x。

这样一来，我们只需要判断所有 occ}(x) 的和与 mid} \times n 的大小关系，就可以在二分查找的过程中调整区间的边界了。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    long long maxRunTime(int n, vector<int>& batteries) {
        long long left = 0, right = accumulate(batteries.begin(), batteries.end(), 0LL) / n, ans = 0;
        while (left <= right) {
            long long mid = (left + right) / 2;
            long long total = 0;
            for (int cap: batteries) {
                total += min(static_cast<long long>(cap), mid);
            }
            if (total >= n * mid) {
                ans = mid;
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }
        return ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def maxRunTime(self, n: int, batteries: List[int]) -> int:
        left, right, ans = 0, sum(batteries) // n, 0
        while left <= right:
            mid = (left + right) // 2
            total = 0
            for cap in batteries:
                total += min(cap, mid)
            if total >= n * mid:
                ans = mid
                left = mid + 1
            else:
                right = mid - 1
        return ans

复杂度分析

  • 时间复杂度：O(n \log C)。其中 C 是数组 batteries 中所有元素的和，在本题中 C 不超过 10^5 \times 10^9 = 10^{14。

  • 空间复杂度：O(1)。

 Comments
On this page
2141-同时运行 N 台电脑的最长时间