2146-价格范围内最高排名的 K 样物品

给你一个下标从 0 开始的二维整数数组 grid ，它的大小为 m x n ，表示一个商店中物品的分布图。数组中的整数含义为：

0 表示无法穿越的一堵墙。
1 表示可以自由通过的一个空格子。
所有其他正整数表示该格子内的一样物品的价格。你可以自由经过这些格子。

从一个格子走到上下左右相邻格子花费 1 步。

同时给你一个整数数组 pricing 和 start ，其中 pricing = [low, high] 且 start = [row, col] ，表示你开始位置为 (row, col) ，同时你只对物品价格在 ** 闭区间** [low, high]
之内的物品感兴趣。同时给你一个整数 k 。

你想知道给定范围内且 排名最高 的 k 件物品的位置。排名按照优先级从高到低的以下规则制定：

距离：定义为从 start 到一件物品的最短路径需要的步数（较近距离的排名更高）。
价格：较低价格的物品有更高优先级，但只考虑在给定范围之内的价格。
行坐标：较小行坐标的有更高优先级。
列坐标：较小列坐标的有更高优先级。

请你返回给定价格内排名最高的 k 件物品的坐标，将它们按照排名排序后返回。如果给定价格内少于 k 件物品，那么请将它们的坐标全部
返回。

示例 1：

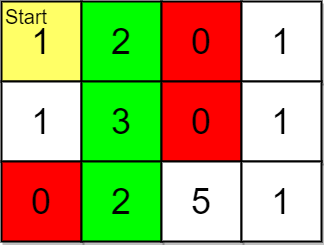
**输入：** grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
**输出：** [[0,1],[1,1],[2,1]]
**解释：** 起点为 (0,0) 。
价格范围为 [2,5] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(2,1) 和 (2,2) 。
这些物品的排名为：
- (0,1) 距离为 1
- (1,1) 距离为 2
- (2,1) 距离为 3
- (2,2) 距离为 4
所以，给定价格范围内排名最高的 3 件物品的坐标为 (0,1)，(1,1) 和 (2,1) 。

示例 2：

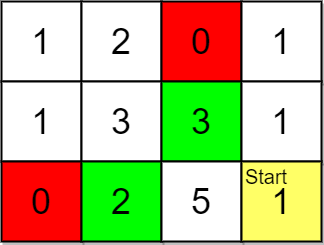
**输入：** grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
**输出：** [[2,1],[1,2]]
**解释：** 起点为 (2,3) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(1,2) 和 (2,1) 。
这些物品的排名为： 
- (2,1) 距离为 2 ，价格为 2
- (1,2) 距离为 2 ，价格为 3
- (1,1) 距离为 3
- (0,1) 距离为 4
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (1,2) 。

示例 3：

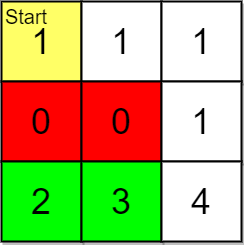
**输入：** grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
**输出：** [[2,1],[2,0]]
**解释：** 起点为 (0,0) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (2,0) 和 (2,1) 。
这些物品的排名为：
- (2,1) 距离为 5
- (2,0) 距离为 6
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (2,0) 。
注意，k = 3 但给定价格范围内只有 2 件物品。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
0 <= grid[i][j] <= 105
pricing.length == 2
2 <= low <= high <= 105
start.length == 2
0 <= row <= m - 1
0 <= col <= n - 1
grid[row][col] > 0
1 <= k <= m * n

方法一：广度优先搜索

思路与算法

根据题意，我们需要求出所有感兴趣物品的距离、价格以及行列坐标。为了求出起点 start 到某件物品的最短路径，我们可以使用广度优先搜索，并在搜索的过程利用数组 items 来统计感兴趣物品的信息。具体地，items 中的每个元素为 (d, \textit{price}, x, y)，其中 d 为物品坐标相对起点的最短距离，price 为物品价格，(x, y) 为物品的行列坐标。

在广度优先搜索的过程中，我们在队列 q 中保存 (x, y, d) 三元组，其中 (x, y) 为当前的行列坐标，d 为当前坐标相对起点的最短距离。

我们首先将起点对应的三元组 (\textit{start}[0], \textit{start}[1], 0) 加入队列。如果起点对应的物品价值在感兴趣的范围内，我们也需要将该物品的相关信息 (0, \textit{grid}[\textit{start}[0]][\textit{start}[1]], \textit{start}[0], \textit{start}[1]) 放入 items 数组。

在遍历到 (x, y) 时，我们枚举它上下左右的相邻坐标 (n_x, n_y)，此时会有以下几种情况：

(n_x, n_y) 不合法或 grid}[n_x][n_y] = 0，此时无需进行任何操作；
grid}[n_x][n_y] = 1 或不在 [\textit{low}, \textit{high}] 区间内，此时该坐标无物品或物品价格不在感兴趣范围内，我们只需将 (n_x, n_y, d + 1) 加入队列 q；
grid}[n_x][n_y] 在 [\textit{low}, \textit{high}] 区间内，此时该坐标的物品在感兴趣的价格范围内，除了需要将 (n_x, n_y, d + 1) 加入队列 q 以外，我们还需要将该物品的距离、价格以及行列坐标 (d + 1, \textit{grid}[n_x][n_y], n_x, n_y) 放入 items 数组。

另外，为了避免重复遍历，我们需要在每个坐标（包括起点）加入队列时将 grid 中对应下标的数值修改为 0。

当遍历完成后，我们将 items 数组按照元素的字典序升序排序，亦即按照优先级从高到低的顺序排序。随后，我们用数组 res 统计 items 数组中前 k 个（若不满即为全部）物品的行列坐标，并将 res 数组返回作为答案。

代码

[sol1-C++]class Solution {
private:
    static constexpr int dx[4] = {1, 0, -1, 0};
    static constexpr int dy[4] = {0, 1, 0, -1};

public:
    vector<vector<int>> highestRankedKItems(vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k) {
        vector<tuple<int, int, int, int>> items;   // 感兴趣物品的信息
        queue<tuple<int, int, int>> q;   // 广度优先搜索队列
        q.emplace(start[0], start[1], 0);
        if (pricing[0] <= grid[start[0]][start[1]] && grid[start[0]][start[1]] <= pricing[1]) {
            items.emplace_back(0, grid[start[0]][start[1]], start[0], start[1]);
        }
        grid[start[0]][start[1]] = 0;   // 避免重复遍历
        int m = grid.size();
        int n = grid[0].size();
        while (!q.empty()) {
            auto [x, y, d] = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                // 遍历相邻坐标，并进行对应操作
                int nx = x + dx[i];
                int ny = y + dy[i];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] > 0) {
                    if (pricing[0] <= grid[nx][ny] && grid[nx][ny] <= pricing[1]) {
                        items.emplace_back(d + 1, grid[nx][ny], nx, ny);
                    }
                    q.emplace(nx, ny, d + 1);
                    grid[nx][ny] = 0;   // 避免重复遍历
                }
            }
        }
        sort(items.begin(), items.end());   // 按照优先级从高到低排序
        vector<vector<int>> res;   // 排名最高 k 件物品的坐标
        int cnt = min(k, static_cast<int>(items.size()));
        for (int i = 0; i < cnt; ++i) {
            auto [d, price, x, y] = items[i];
            res.push_back({x, y});
        }
        return res;
    }
};

[sol1-Python3]class Solution:
    def highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:
        items = []   # 感兴趣物品的信息
        q = deque([(start[0], start[1], 0)])   # 广度优先搜索队列
        if pricing[0] <= grid[start[0]][start[1]] <= pricing[1]:
            items.append([0, grid[start[0]][start[1]], start[0], start[1]])
        grid[start[0]][start[1]] = 0   # 避免重复遍历
        m = len(grid)
        n = len(grid[0])
        dx = [1, 0, -1, 0]
        dy = [0, 1, 0, -1]
        while q:
            x, y, d = q.popleft()
            for i in range(4):
                # 遍历相邻坐标，并进行对应操作
                nx, ny = x + dx[i], y + dy[i]
                if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] > 0:
                    q.append((nx, ny, d + 1))
                    if pricing[0] <= grid[nx][ny] <= pricing[1]:
                        items.append([d + 1, grid[nx][ny], nx, ny])
                    grid[nx][ny] = 0   # 避免重复遍历
        items.sort()   # 按照优先级从高到低排序
        res = [item[2:] for item in items][:k]   # 排名最高 k 件物品的坐标
        return res

复杂度分析

时间复杂度：O(mn \log(mn))，其中 m, n 为 grid 的行数与列数。其中广度优先搜索求出可选择物品的时间复杂度为 O(mn)，对物品按要求排序的时间复杂度为 O(mn \log(mn))。
空间复杂度：O(mn)，即为保存符合要求物品信息的辅助数组的空间开销。