2147-分隔长廊的方案数
在一个图书馆的长廊里,有一些座位和装饰植物排成一列。给你一个下标从 0 开始,长度为 n 的字符串 corridor ,它包含字母'S' 和 'P' ,其中每个 'S' 表示一个座位,每个 'P' 表示一株植物。
在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i
之间(1 <= i <= n - 1),至多能放一个屏风。
请你将走廊用屏风划分为若干段,且每一段内都 恰好有两个座位
,而每一段内植物的数目没有要求。可能有多种划分方案,如果两个方案中有任何一个屏风的位置不同,那么它们被视为 不同 方案。
请你返回划分走廊的方案数。由于答案可能很大,请你返回它对 109 + 7 取余 的结果。如果没有任何方案,请返回 0 。
示例 1:
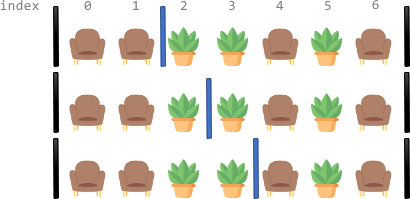
**输入:** corridor = "SSPPSPS"
**输出:** 3
**解释:** 总共有 3 种不同分隔走廊的方案。
上图中黑色的竖线表示已经放置好的屏风。
上图每种方案中,每一段都恰好有 **两个** 座位。
示例 2:

**输入:** corridor = "PPSPSP"
**输出:** 1
**解释:** 只有 1 种分隔走廊的方案,就是不放置任何屏风。
放置任何的屏风都会导致有一段无法恰好有 2 个座位。
示例 3:
**输入:** corridor = "S"
**输出:** 0
**解释:** 没有任何方案,因为总是有一段无法恰好有 2 个座位。
提示:
n == corridor.length1 <= n <= 105corridor[i]要么是'S',要么是'P'。
方法一:乘法原理
思路与算法
我们可以按照顺序将座位每两个分成一组。在相邻两组之间,如果有 x 个装饰植物,那么就有 x + 1 种放置屏风的方法。根据乘法原理,总方案数就是所有 x+1 的乘积。
因此,我们只需要对数组 corridor 进行一次遍历就可得到答案。在遍历的过程中,我们维护当前的座位总数 cnt 和上一个座位的位置 prev。当遍历到 corridor}[i] 时,如果它是座位,并且包括它我们遍历到奇数(并且大于等于 3)个座位,那么 corridor}[i] 就是一个新的座位组的开始,它和上一个组之间就有 i - \textit{prev} - 1 个装饰植物,即 i - \textit{prev 种放置屏风的方法。
在遍历完成后,我们需要检查 cnt 是否为偶数并且大于等于 2。如果不满足,那么需要返回 0。
代码
1 | class Solution { |
1 | class Solution: |
1 | func numberOfWays(corridor string) int { |
复杂度分析
时间复杂度:O(n)。
空间复杂度:O(1)。