2162-设置时间的最少代价

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

常见的微波炉可以设置加热时间，且加热时间满足以下条件：

  • 至少为 1 秒钟。
  • 至多为 99 分 99 秒。

你可以 最多 输入 4 个数字 来设置加热时间。如果你输入的位数不足 4 位，微波炉会自动加 前缀 0 来补足
4 位。微波炉会将设置好的四位数中， 前 两位当作分钟数， 后 两位当作秒数。它们所表示的总时间就是加热时间。比方说：

  • 你输入 9 5 4 （三个数字），被自动补足为 0954 ，并表示 9 分 54 秒。
  • 你输入 0 0 0 8 （四个数字），表示 0 分 8 秒。
  • 你输入 8 0 9 0 ，表示 80 分 90 秒。
  • 你输入 8 1 3 0 ，表示 81 分 30 秒。

给你整数 startAt ，moveCost ，pushCost 和 targetSeconds 。 一开始 ，你的手指在数字
startAt 处。将手指移到 ** 任何其他数字** ，需要花费 moveCost 的单位代价。 每
输入你手指所在位置的数字一次，需要花费 pushCost 的单位代价。

要设置 targetSeconds 秒的加热时间，可能会有多种设置方法。你想要知道这些方法中，总代价最小为多少。

请你能返回设置 targetSeconds 秒钟加热时间需要花费的最少代价。

请记住，虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒。

示例 1：

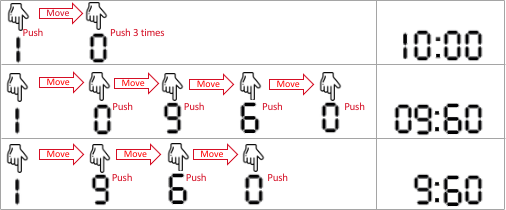
**输入：** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**输出：** 6
**解释：** 以下为设置加热时间的所有方法。
- 1 0 0 0 ，表示 10 分 0 秒。
  手指一开始就在数字 1 处，输入 1 （代价为 1），移到 0 处（代价为 2），输入 0（代价为 1），输入 0（代价为 1），输入 0（代价为 1）。
  总代价为：1 + 2 + 1 + 1 + 1 = 6 。这是所有方案中的最小代价。
- 0 9 6 0，表示 9 分 60 秒。它也表示 600 秒。
  手指移到 0 处（代价为 2），输入 0 （代价为 1），移到 9 处（代价为 2），输入 9（代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12 。
- 9 6 0，微波炉自动补全为 0960 ，表示 9 分 60 秒。
  手指移到 9 处（代价为 2），输入 9 （代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 = 9 。

示例 2：

**输入：** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**输出：** 6
**解释：** 最优方案为输入两个数字 7 6，表示 76 秒。
手指移到 7 处（代价为 1），输入 7 （代价为 2），移到 6 处（代价为 1），输入 6（代价为 2）。总代价为：1 + 2 + 1 + 2 = 6
其他可行方案为 0076 ，076 ，0116 和 116 ，但是它们的代价都比 6 大。

提示：

  • 0 <= startAt <= 9
  • 1 <= moveCost, pushCost <= 105
  • 1 <= targetSeconds <= 6039

方法一：模拟

提示 1

对于某一个目标秒数，至多只有两种按键方案有可能是最优的。

提示 1 解释

首先，对于某一种带有前导零的（四位数字）输入，不输入前导零显然是更优的。

我们用 m, s 来表示四位输入的前两位和后两位。根据题意，我们有 0 \le m, s \le 99。如果确定了 m, s，那么对应的最优操作方式也可以确定，即移动次数最少的方式（此时按键次数已确定）。

同时，我们用 mm}, \textit{ss} (0 \le \textit{ss} \le 59) 来唯一表示目标时间对应的分和秒数。那么，我们有：

\textit{targetSeconds} = 60 \times m + s = 60 \times \textit{mm} + \textit{ss}.

进一步，考虑到各个变量的取值范围，我们可以得到两组变量所有可能的对应关系：

  • m = \textit{mm}, s = \textit{ss；

  • m = \textit{mm} - 1, s = \textit{ss} + 60。

其中「可能」指的是如果上述关系可以使得每个变量均满足取值范围要求，则该对应关系成立。

那么，最优的方案只能是上述两种（如果存在）中花费较小的方案。

思路与算法

根据 提示 1，我们只需要计算上述两种方案对应的最小花费即可。

我们用函数 cost}(m, s) 模拟对应的方案，并计算 m, s 确定的输入的最小花费。

首先我们用数组 digits 按顺序表示四位输入的每一位。在模拟之前，我们需要找到 digits 中第一个非零位 start，并以该位作为起始点。

我们用 res 来表示总花费，并用 prev 来表示当前手指的位置，prev 的初值即为 startAt。在顺序遍历 digits 中 start 以后的整数位 d 时，我们首先判断当前位与手指位置是否相等：如果相等，则不需要移动；如果不相等，则需要令 prev} = d，同时将 res 加上单次移动的花费 moveCost。随后，我们还需要将 res 加上单次按键的花费 pushCost。

当遍历完成后，res 即为对应的最小花费，我们返回该值作为答案。

对于两种方案，我们首先判断取值范围，如果合法，则计算对应的最小花费。最终，我们返回所有可行的花费中较小的作为答案。

细节

为了方便判断 m, s 的合法性，我们可以在函数 cost}(m, s) 中对于不合法的 m, s 返回一个极大的数即可。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
        // 给定输入的最小花费
        auto cost = [&](int m, int s) -> int {
            if (m < 0 || m > 99 || s < 0 || s > 99) {
                // 输入不合法
                return INT_MAX;
            }
            vector<int> digits = {m / 10, m % 10, s / 10, s % 10};
            // 寻找起始位
            int start = 0;
            while (start < 4 && digits[start] == 0) {
                ++start;
            }
            
            int res = 0;   // 最小花费
            int prev = startAt;
            for (int i = start; i < 4; ++i) {
                int d = digits[i];
                if (d != prev) {
                    // 此时需要先移动再输入
                    prev = d;
                    res += moveCost;
                }
                res += pushCost;
            }
            return res;
        };
        
        int mm = targetSeconds / 60, ss = targetSeconds % 60;
        return min(cost(mm, ss), cost(mm - 1, ss + 60));   // 两种可能方案的较小值
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def minCostSetTime(self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int) -> int:
        # 给定输入的最小花费
        def cost(m: int, s: int) -> int:
            if not (0 <= m <= 99 and 0 <= s <= 99):
                # 输入不合法
                return float("INF")
            digits = [m // 10, m % 10, s // 10, s % 10]
            # 寻找起始位
            start = 0
            while start < 4 and digits[start] == 0:
                start += 1
            
            res = 0   # 最小花费
            prev = startAt
            for d in digits[start:]:
                if d != prev:
                    # 此时需要先移动再输入
                    prev = d
                    res += moveCost
                res += pushCost
            return res
        
        mm, ss = targetSeconds // 60, targetSeconds % 60
        return min(cost(mm, ss), cost(mm - 1, ss + 60))   # 两种可能方案的较小值

复杂度分析

  • 时间复杂度：O(1)。

  • 空间复杂度：O(1)。

 Comments
On this page
2162-设置时间的最少代价