2196-根据描述创建二叉树

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

给你一个二维整数数组 descriptions ，其中 descriptions[i] = [parenti, childi, isLefti]
表示 parenti 是 childi 在 二叉树 中的 父节点 ，二叉树中各节点的值 互不相同 。此外：

  • 如果 isLefti == 1 ，那么 childi 就是 parenti 的左子节点。
  • 如果 isLefti == 0 ，那么 childi 就是 parenti 的右子节点。

请你根据 descriptions 的描述来构造二叉树并返回其 根节点 。

测试用例会保证可以构造出 有效 的二叉树。

示例 1：

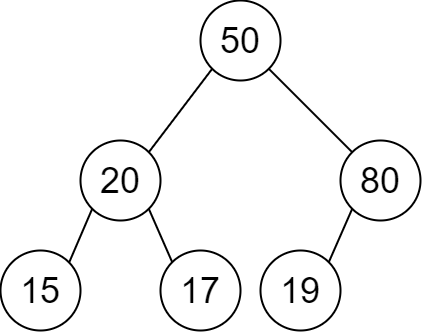
**输入：** descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
**输出：** [50,20,80,15,17,19]
**解释：** 根节点是值为 50 的节点，因为它没有父节点。
结果二叉树如上图所示。

示例 2：

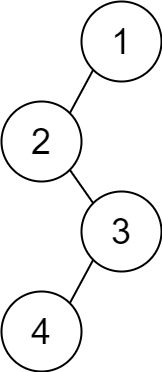
**输入：** descriptions = [[1,2,1],[2,3,0],[3,4,1]]
**输出：** [1,2,null,null,3,4]
**解释：** 根节点是值为 1 的节点，因为它没有父节点。 
结果二叉树如上图所示。

提示：

  • 1 <= descriptions.length <= 104
  • descriptions[i].length == 3
  • 1 <= parenti, childi <= 105
  • 0 <= isLefti <= 1
  • descriptions 所描述的二叉树是一棵有效二叉树

方法一：哈希表

思路与算法

由于数组 descriptions 中用节点的数值表示对应节点，因此为了方便查找，我们用哈希表 nodes 来维护数值到对应节点的映射。

我们可以遍历数组 descriptions 来创建二叉树。具体地，当我们遍历到三元组 [p, c, \textit{left}] 时，我们首先判断 nodes 中是否存在 p 与 c 对应的树节点，如果没有则我们新建一个数值为对应值的节点。随后，我们根据 left 的真假将 p 对应的节点的左或右子节点设为 c 对应的节点。当遍历完成后，我们就重建出了目标二叉树。

除此之外，我们还需要寻找二叉树的根节点。这个过程也可以在遍历和建树的过程中完成。我们可以同样用一个哈希表 isRoot 维护数值与是否为根节点的映射。在遍历时，我们需要将 isRoot}[c] 设为 false（因为该节点有父节点）；而如果 p 在 isRoot 中不存在，则说明 p 暂时没有父节点，我们可以将 isRoot}[c] 设为 true。最终在遍历完成后，一定有且仅有一个元素 root 在 isRoot 中的数值为 true，此时对应的 node}[i] 为二叉树的根节点，我们返回该节点作为答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        unordered_map<int, bool> isRoot;   // 数值对应的节点是否为根节点的哈希表
        unordered_map<int, TreeNode*> nodes;   // 数值与对应节点的哈希表
        for (const auto& d: descriptions) {
            int p = d[0];
            int c = d[1];
            bool left = d[2];
            if (!isRoot.count(p)) {
                isRoot[p] = true;
            }
            isRoot[c] = false;
            // 创建或更新节点
            if (!nodes.count(p)) {
                nodes[p] = new TreeNode(p);
            }
            if (!nodes.count(c)) {
                nodes[c] = new TreeNode(c);
            }
            if (left) {
                nodes[p]->left = nodes[c];
            } else {
                nodes[p]->right = nodes[c];
            }
        }
        // 寻找根节点
        int root = -1;
        for (const auto& [val, r]: isRoot) {
            if (r) {
                root = val;
                break;
            }
        }
        return nodes[root];
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:
        isRoot = {}   # 数值对应的节点是否为根节点的哈希表
        nodes = {}   # 数值与对应节点的哈希表
        for p, c, left in descriptions:
            if p not in isRoot:
                isRoot[p] = True
            isRoot[c] = False
            # 创建或更新节点
            if p not in nodes:
                nodes[p] = TreeNode(p)
            if c not in nodes:
                nodes[c] = TreeNode(c)
            if left:
                nodes[p].left = nodes[c]
            else:
                nodes[p].right = nodes[c]
        # 寻找根节点
        root = -1
        for val, r in isRoot.items():
            if r:
                root = val
                break
        return nodes[root]

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组 descriptions 的长度。即为遍历构造二叉树并寻找根节点的时间复杂度。

  • 空间复杂度：O(n)，即为哈希表的空间开销。

 Comments
On this page
2196-根据描述创建二叉树