2201-统计可以提取的工件
存在一个 n x n 大小、下标从 0 开始的网格,网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组artifacts ,artifacts 描述了矩形工件的位置,其中 artifacts[i] = [r1i, c1i, r2i, c2i]
表示第 i 个工件在子网格中的填埋情况:
(r1i, c1i)是第i个工件 左上 单元格的坐标,且(r2i, c2i)是第i个工件 右下 单元格的坐标。
你将会挖掘网格中的一些单元格,并清除其中的填埋物。如果单元格中埋着工件的一部分,那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来,你就可以提取该工件。
给你一个下标从 0 开始的二维整数数组 dig ,其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci)
,返回你可以提取的工件数目。
生成的测试用例满足:
- 不存在重叠的两个工件。
- 每个工件最多只覆盖
4个单元格。 dig中的元素互不相同。
示例 1:
**输入:** n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
**输出:** 1
**解释:**
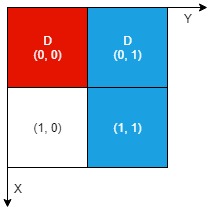
不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。
有 1 个工件可以提取,即红色工件。
蓝色工件在单元格 (1,1) 的部分尚未裸露出来,所以无法提取该工件。
因此,返回 1 。
示例 2:
**输入:** n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
**输出:** 2
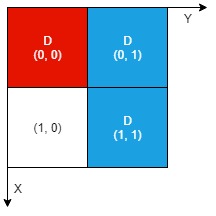
**解释:** 红色工件和蓝色工件的所有部分都裸露出来(用 'D' 标记),都可以提取。因此,返回 2 。
提示:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2, 105)artifacts[i].length == 4dig[i].length == 20 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1r1i <= r2ic1i <= c2i- 不存在重叠的两个工件
- 每个工件 最多 只覆盖
4个单元格 dig中的元素互不相同
方法一:使用哈希表存储挖掘的位置
思路与算法
我们首先遍历数组 digs,并使用哈希集合存储其中的每一个位置。
随后我们遍历数组 artifacts 中的每一个工件,由于「每个工件最多只覆盖 4 个单元格」,我们可以直接遍历每一个工件的每一个单元格,如果该工件的所有单元格都在哈希集合中,我们就可以提取该工件。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(C \cdot a + d),其中 a 和 d 分别是数组 artifacts 和 dig 的长度,C 是每个工件最多覆盖的单元格数,在本题中 C=4。
空间复杂度:O(d),即为哈希表需要使用的空间。
Comments