2212-射箭比赛中的最大得分
Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下:
- Alice 先射
numArrows支箭,然后 Bob 也射numArrows支箭。 - 分数按下述规则计算:
1. 箭靶有若干整数计分区域,范围从0到11(含0和11)。
2. 箭靶上每个区域都对应一个得分k(范围是0到11),Alice 和 Bob 分别在得分k区域射中ak和bk支箭。如果ak >= bk,那么 Alice 得k分。如果ak < bk,则 Bob 得k分
3. 如果ak == bk == 0,那么无人得到k分。
- 例如,Alice 和 Bob 都向计分为
11的区域射2支箭,那么 Alice 得11分。如果 Alice 向计分为11的区域射0支箭,但 Bob 向同一个区域射2支箭,那么 Bob 得11分。
给你整数 numArrows 和一个长度为 12 的整数数组 aliceArrows ,该数组表示 Alice 射中 0 到 11
每个计分区域的箭数量。现在,Bob 想要尽可能 最大化 他所能获得的总分。
返回数组 bobArrows __ ,该数组表示 Bob 射中 0 到 11 每个 计分区域的箭数量。且 bobArrows
的总和应当等于 numArrows 。
如果存在多种方法都可以使 Bob 获得最大总分,返回其中 任意一种 即可。
示例 1:
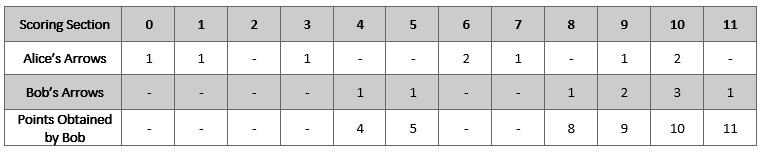
**输入:** numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
**输出:** [0,0,0,0,1,1,0,0,1,2,3,1]
**解释:** 上表显示了比赛得分情况。
Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。
可以证明 Bob 无法获得比 47 更高的分数。
示例 2:

**输入:** numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
**输出:** [0,0,0,0,0,0,0,0,1,1,1,0]
**解释:** 上表显示了比赛得分情况。
Bob 获得总分 8 + 9 + 10 = 27 。
可以证明 Bob 无法获得比 27 更高的分数。
提示:
1 <= numArrows <= 105aliceArrows.length == bobArrows.length == 120 <= aliceArrows[i], bobArrows[i] <= numArrowssum(aliceArrows[i]) == numArrows
方法一:枚举状态
思路与算法
为了最大化地利用箭,我们需要在每个需要获胜的区域都用尽可能少的箭数取胜。具体而言,对于第 i 个区域,我们只需要使用 aliceArrows}[i] + 1 支箭即可。
为了计算可能获得的最大得分及对应方法,一种方法是,枚举所有区域可能的胜负情况,并计算该情况的得分与最少需要的箭数,并判断是否可行。与此同时,我们维护可能的最大得分 maxscore 以及对应的胜负情况。最终,我们利用胜负情况构造出任意一种方法并返回即可。
由于每个区域只有 Bob 胜或负两种情况,因此我们可以用一个 n 位的二进制整数 mask 表示所有区域的胜负情况,其中第 i 位为 0 代表 Bob 在得分为 i 的区域中落败,为 1 则代表 Bob 在该区域取胜。
在维护最大得分 maxscore 的同时,我们还维护最大得分对应的二进制状态 state。我们遍历 mask 的所有可能取值,即 [0, 2^n - 1] 闭区间内的所有整数,对于每个 mask,我们遍历它的每一位计算该状态对应的得分 score 和最少需要箭数 cnt。如果该状态可以达成,即 cnt \le \textit{numArrows,且该状态刷新了当前可行的最大得分 score} > \textit{maxscore,则我们更新最大得分 maxscore 与对应状态 state。
最终,我们尝试通过最大得分对应状态 state 构造一种可行的方法。具体地,我们用长度为 n 的数组 res 表示这一方法。首先,我们枚举每下标 i,判断该区域 Bob 是否取胜,如果是,则 res}[i] = \textit{aliceArrows}[i] + 1;反之则为 0。最终,如果箭还有剩余,我们可以将它放入任意的区域中,在这里我们将它放入第 0 个区域。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(n \times 2^n),其中 n 为箭靶的数量,在本题中 n = 12。所有的得分状态共有 2^n 种,对于单个状态,判断是否可行以及维护最大得分的时间复杂度为 O(n)。
空间复杂度:O(1)。