2250-统计包含每个点的矩形数目

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:27 2023-09-13 16:06:27 Updated    

给你一个二维整数数组 rectangles ，其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为
hi 。给你一个二维整数数组 points ，其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。

第 i 个矩形的 左下角 在 (0, 0) 处， 右上角 在 (li, hi) 。

请你返回一个整数数组 _ _count ，长度为 points.length，其中 _ _count[j]是 包含 第 _ _j
个点的矩形数目。

如果 0 <= xj <= li 且 0 <= yj <= hi ，那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的
边上 ，这个点也被视为被矩形包含。

示例 1：

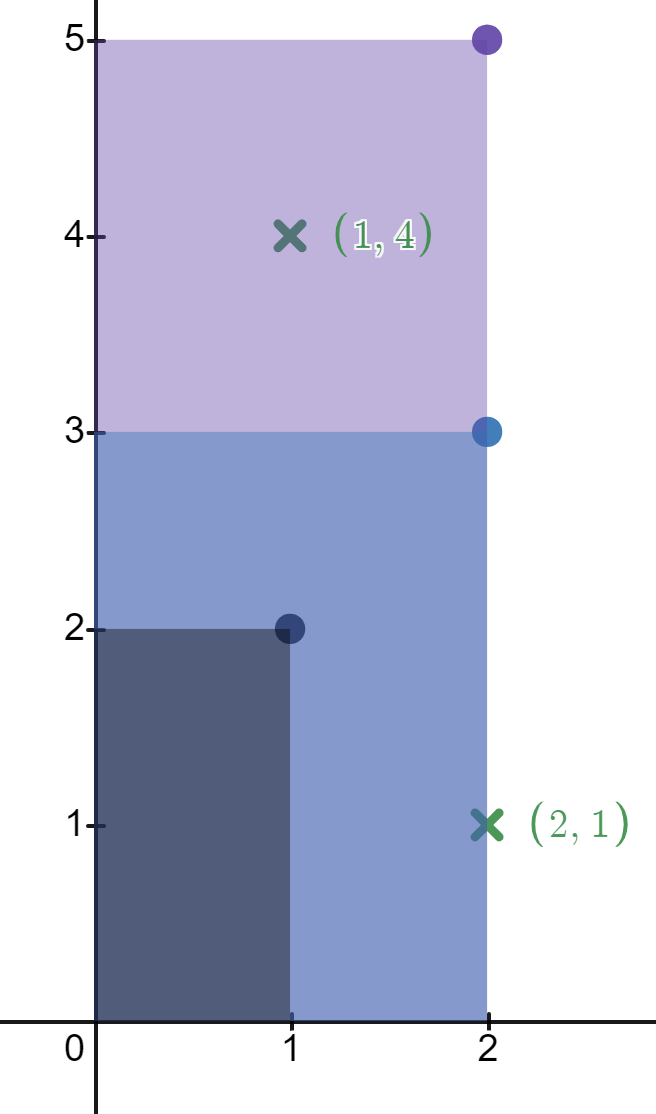
**输入：** rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
**输出：** [2,1]
**解释：**
第一个矩形不包含任何点。
第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以，我们返回 [2, 1] 。

示例 2：

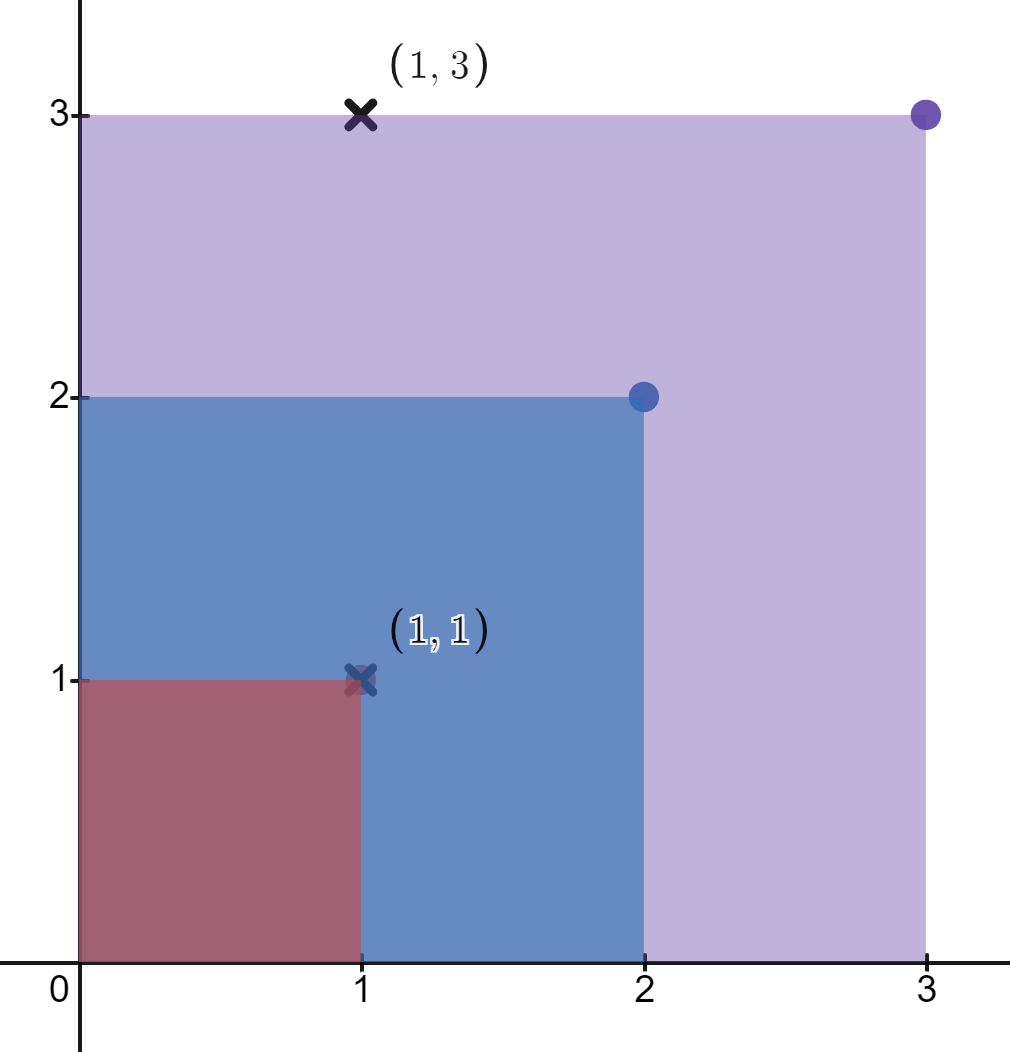
**输入：** rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
**输出：** [1,3]
**解释：** 第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以，我们返回 [1, 3] 。

提示：

  • 1 <= rectangles.length, points.length <= 5 * 104
  • rectangles[i].length == points[j].length == 2
  • 1 <= li, xj <= 109
  • 1 <= hi, yj <= 100
  • 所有 rectangles 互不相同 。
  • 所有 points 互不相同 。

方法一：按照纵坐标分组

思路与算法

我们用 m 表示矩形的个数，用 n 表示点的个数。如果对于每个点，我们都遍历所有矩形计算包含的矩形数目，则总共的时间复杂度为 O(mn)，不符合题目的要求。因此我们需要优化计算的过程。

容易发现，所有点的纵坐标都位于 [1, 100] 闭区间的范围。对于相同纵坐标的点，我们可以只遍历一次所有的矩形并保存所有高度大于等于该坐标的矩形的长度。随后，我们就可以通过对排序后数组二分查找的方式计算出包含对应点矩形的数目。

具体地，我们首先用哈希表维护每个纵坐标对应点的横坐标和在 points 数组的下标。维护下标是为了便于最终恢复结果。与此同时，我们用数组 res 记录包含每个点的矩形数目。随后，对于每个纵坐标 y，我们用函数 lengths}(y) 遍历所有矩形，记录所有高度大于等于 y 的矩形的长度，并以升序返回。得到长度数组后，我们遍历该纵坐标对应的所有点，并通过二分查找计算能够覆盖该坐标的矩形数量，并填入 res 数组的对应位置。此时假设长度数组的长度为 l，第一个长度大于等于该点横坐标的的下标为 i，则可以覆盖该点的矩形数量为 l - i。最终，我们返回 res 数组作为答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        int n = points.size();
        vector<int> res(n);   // 记录结果
        unordered_map<int, vector<pair<int, int>>> p;   // 记录每个纵坐标对应点的横坐标与下标
        for (int i = 0; i < n; ++i) {
            p[points[i][1]].emplace_back(points[i][0], i);
        }
        // 计算高度大于每个纵坐标的所有矩形的长度，并以升序返回
        auto lengths = [&](int y) -> vector<int> {
            vector<int> res;
            for (const auto& rect: rectangles) {
                if (rect[1] >= y) {
                    res.push_back(rect[0]);
                }
            }
            sort(res.begin(), res.end());
            return res;
        };

        for (const auto& [h, plist]: p) {
            vector<int> llist = lengths(h);
            for (const auto& [x, idx]: plist) {
                // 二分查找计算覆盖矩形数量并更新结果数组
                res[idx] = llist.end() - lower_bound(llist.begin(), llist.end(), x);
            }
        }
        return res;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:
        n = len(points)
        res = [0] * n   # 记录结果
        p = defaultdict(list)   # 记录每个纵坐标对应点的横坐标与下标
        for i in range(n):
            p[points[i][1]].append((points[i][0], i))
        # 计算高度大于每个纵坐标的所有矩形的长度，并以升序返回
        def lengths(y: int):
            res = []
            for l, h in rectangles:
                if h >= y:
                    res.append(l)
            return sorted(res)
        
        # 遍历所有纵坐标
        for h, plist in p.items():
            llist = lengths(h)
            for x, idx in plist:
                # 二分查找计算覆盖矩形数量并更新结果数组
                res[idx] = len(llist) - bisect.bisect_left(llist, x)
        return res

复杂度分析

  • 时间复杂度：O(hm\log m + n\log m)，其中 h 为纵坐标范围大小，m 为 rectangles 数组的长度，n 为 points 数组的长度。对于每个高度遍历矩形数组并排序的时间复杂度为 O(m\log m)，共需遍历 O(h) 次；二分查找计算每个点覆盖矩形数量的时间复杂度为 O(\log m)，共需计算 O(n) 次。

  • 空间复杂度：O(m + n)，即为哈希表和矩形长度数组的空间开销。

 Comments
On this page
2250-统计包含每个点的矩形数目