2257-统计网格图中没有被保卫的格子数
给你两个整数 m 和 n 表示一个下标从 ** 0** 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和walls ,其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ,分别表示第 i
个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向(即东、南、西、北)的 所有 格子,除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被
至少 一个警卫看到,那么我们说这个格子被 保卫 了。
请你返回空格子中,有多少个格子是 没被保卫 的。
示例 1:
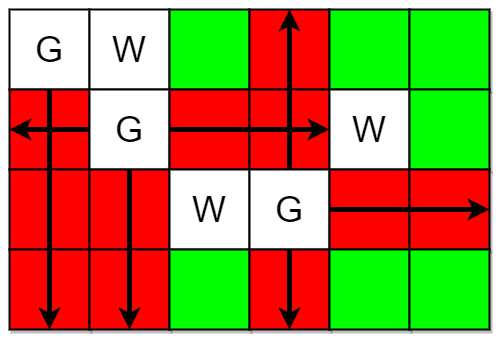
**输入:** m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
**输出:** 7
**解释:** 上图中,被保卫和没有被保卫的格子分别用红色和绿色表示。
总共有 7 个没有被保卫的格子,所以我们返回 7 。
示例 2:
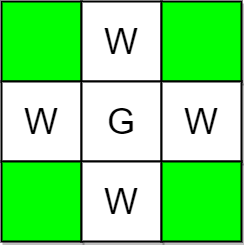
**输入:** m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
**输出:** 4
**解释:** 上图中,没有被保卫的格子用绿色表示。
总共有 4 个没有被保卫的格子,所以我们返回 4 。
提示:
1 <= m, n <= 1052 <= m * n <= 1051 <= guards.length, walls.length <= 5 * 1042 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < nguards和walls中所有位置 互不相同 。
方法一:广度优先搜索 + 存储每个格子的状态
思路与算法
为了方便操作,我们可以用二维数组 grid 来表示网格图的状态。其中,警卫对应的状态值为 -1,墙对应的状态值为 -2,未被保卫的格子对应的状态值为 0,被保卫格子对应的状态值为正整数。二维数组的初始值均为 0,随后我们遍历 guards 和 walls 数组对应更新网格图。
在恢复了网格图后,我们可以使用广度优先搜索维护每个格子的状态。由于视线是向特定方向的,因此在广度优先搜索的过程中,除了要维护格子的横纵坐标,还要维护当前的视线方向。我们用 (i, j, k) 来表示广度优先搜索的状态,其中 (i, j) 代表当前点的横纵坐标,k 为 [0, 3] 闭区间内的整数,分别代表右、上、左、下的视线方向。同样地,为了防止每个非警卫或墙的点被重复或遗漏,我们用 4 个二进制位组成的正整数来表示该格子的状态,其中从低到高的第 k 位为 1 代表有指向第 k 个方向的视线经过该点,反之则代表没有。
我们用队列 q 来进行广度优先搜索。首先,对于每个警卫点 (i, j),由于警卫可以看到四个方向,因此我们需要将 k 为 [0, 3] 闭区间内对应的四种状态 (i, j, k) 全部加进队列。
当遍历到 (x, y, k) 时,我们首先计算沿着该视线方向的下一个坐标 (n_x, n_y),如果该坐标不合法或为墙或警卫,则我们直接跳过该坐标;对于余下的情况,我们需要检查该坐标对应状态 grid}[i][j] 中从低到高的第 k 位的数值。此时有两种情况:
第 k 位为 1,则说明该坐标及视线方向对应的状态 (n_x, n_y, k) 已被遍历过,我们直接跳过即可;
第 k 位为 0,则说明该坐标及视线方向对应的状态 (n_x, n_y, k) 未被遍历过,我们需要将该位置为 1,并将该状态加入队列 q 的尾部。
最终,当广度优先搜索完成时,一个格子未被保卫当且仅当 grid 中的对应状态值为 0。我们只需要遍历 grid,维护数值为 0 的格子数量,并返回即可。
代码
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(mn),其中 m 和 n 分别为网格图的行数与列数。即为广度优先搜索的时间复杂度。
空间复杂度:O(mn),即为网格图数组的空间开销。