2280-表示一个折线图的最少线段数

给你一个二维整数数组 stockPrices ，其中 stockPrices[i] = [dayi, pricei] 表示股票在 dayi
的价格为 pricei 。 折线图
是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

![](https://assets.leetcode.com/uploads/2022/03/30/1920px-
pushkin_population_historysvg.png)

请你返回要表示一个折线图所需要的 最少线段数 。

示例 1：

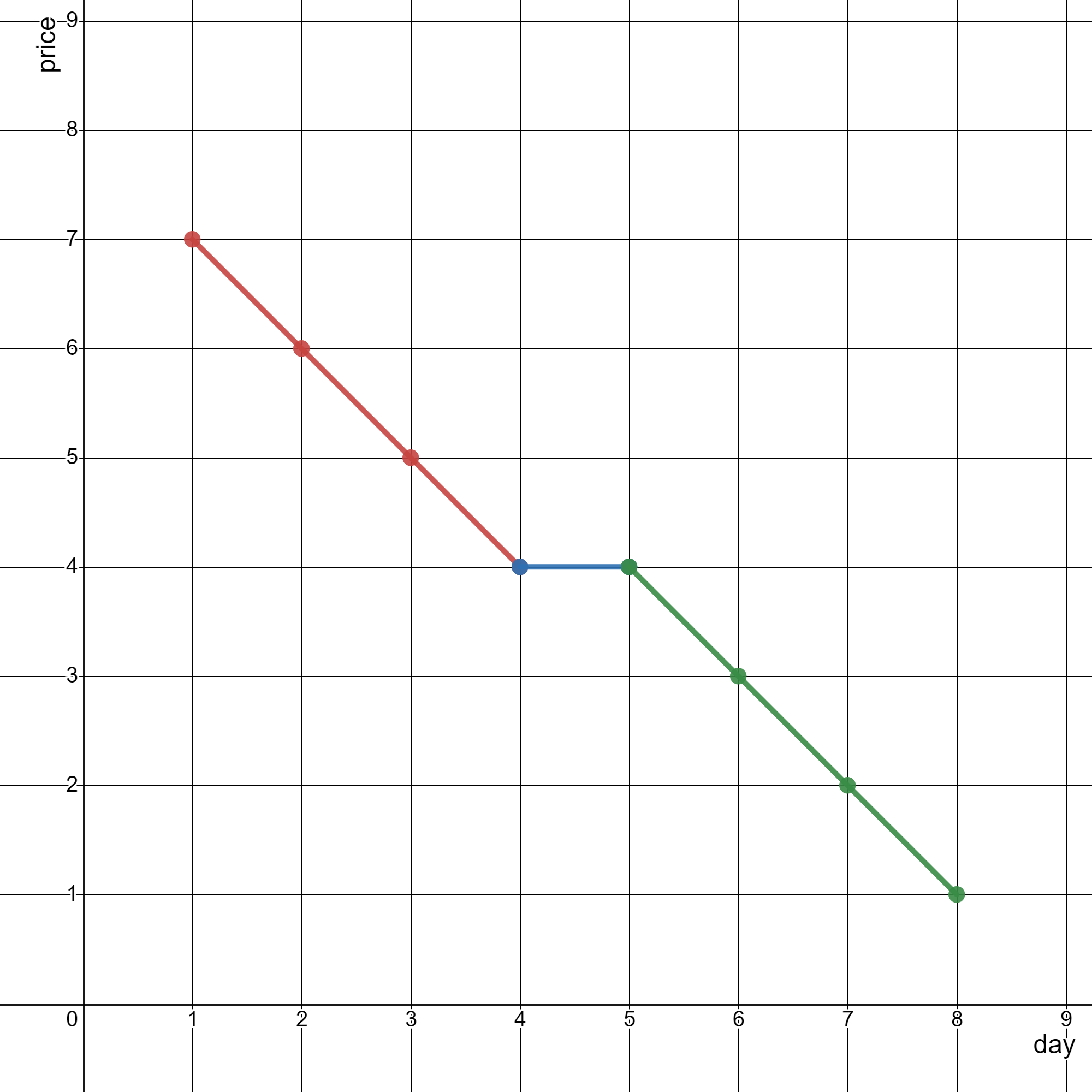
**输入：** stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
**输出：** 3
**解释：**
上图为输入对应的图，横坐标表示日期，纵坐标表示价格。
以下 3 个线段可以表示折线图：
- 线段 1 （红色）从 (1,7) 到 (4,4) ，经过 (1,7) ，(2,6) ，(3,5) 和 (4,4) 。
- 线段 2 （蓝色）从 (4,4) 到 (5,4) 。
- 线段 3 （绿色）从 (5,4) 到 (8,1) ，经过 (5,4) ，(6,3) ，(7,2) 和 (8,1) 。
可以证明，无法用少于 3 条线段表示这个折线图。

示例 2：

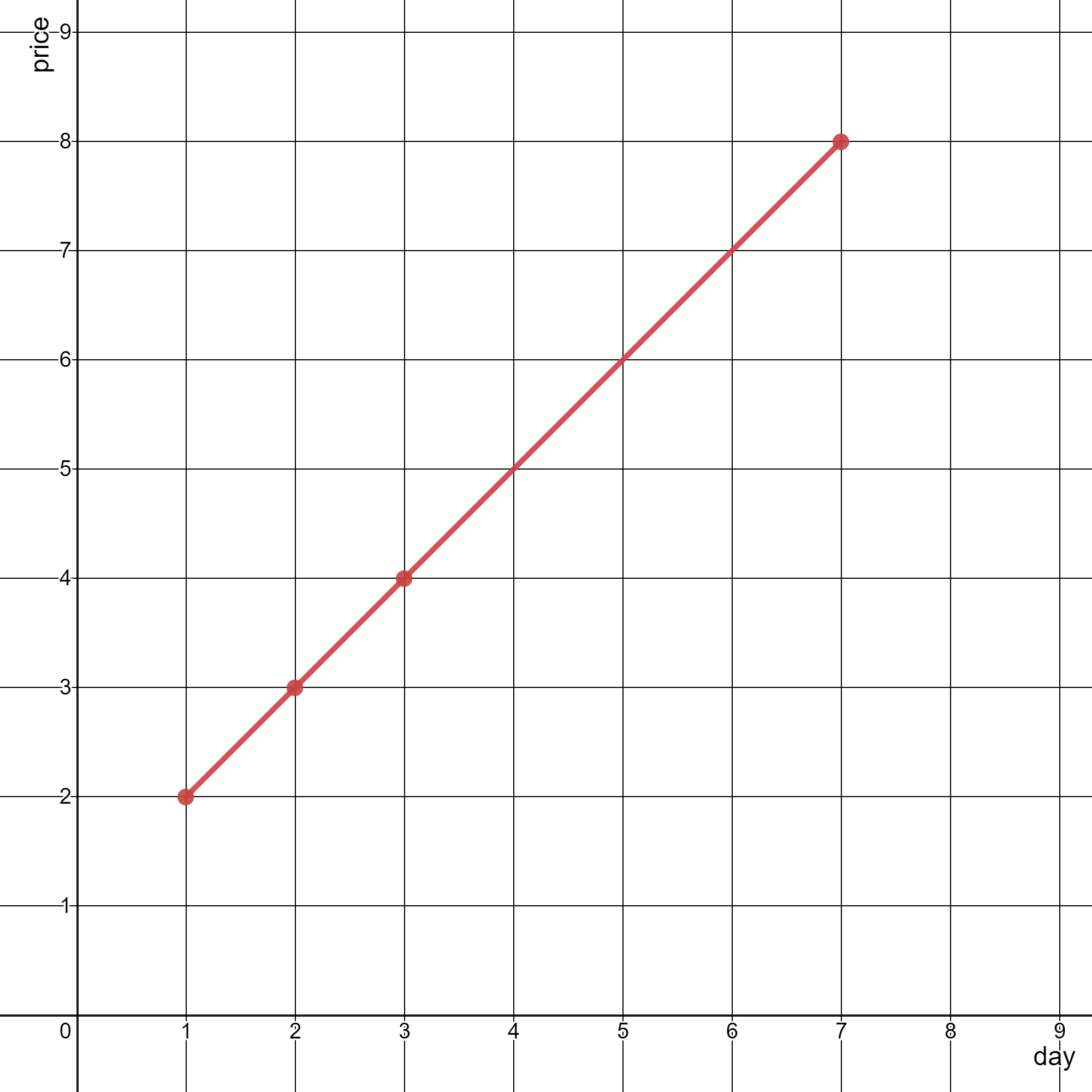
**输入：** stockPrices = [[3,4],[1,2],[7,8],[2,3]]
**输出：** 1
**解释：**
如上图所示，折线图可以用一条线段表示。

提示：

• 1 <= stockPrices.length <= 105
• stockPrices[i].length == 2
• 1 <= dayi, pricei <= 109
• 所有 dayi 互不相同 。

方法一：排序 + 遍历统计

思路与算法

首先，我们将折线图的点按照横坐标升序排序。排序后数组 stockPrices 中的相邻格点连成的线段即组成了折线图。

我们用 n 来表示折线图的点数，并用 res 统计表示折线图所需的最少线段数。当 n \le 2 时，折线图的表示方式唯一，即需要 n - 1 条线段表示。当 n > 2 时，我们可以从左至右遍历每一对相邻的点对，并判断该点对组成的折线是否可以与前面相邻的折线（如有）合并，进而计算最少的线段数。

具体地，我们令 res 的初始值为 1（代表 stockPrices}[0] 与 stockPrices}[1] 构成的线段），随后，我们从 i = 2 开始遍历相邻点对，并判断 stockPrices}[i] 与 stockPrices}[i - 1] 构成的线段是否可以与前一组相邻点对 stockPrices}[i - 1] 与 stockPrices}[i - 2] 构成的线段合并，即两条线段的斜率是否相等。

我们用 dx}_0, \textit{dy}_0 表示前一组相邻点对的横纵坐标差，用 dx}_1, \textit{dy}_1 表示当前相邻点对的横纵坐标差。则两组线段的斜率分别为 dy}_0/\textit{dx}_0 与 dy}_1/\textit{dx}_1。此时如果两组线段斜率不相等，则代表两条线段不可以合并，我们将 res 加上 1；反之则代表可以合并，我们无需进行任何操作。

当遍历完成所有相邻点对后，res 即为最少的线段数，我们返回该数值作为答案。

细节

在比较斜率 dy}_0/\textit{dx}_0 与 dy}_1/\textit{dx}_1 时，为了避免浮点数的精度造成误差，我们可以对两边进行通分，即判断 dx}_0 \times \textit{dy}_1 与 dx}_1 \times \textit{dy}_0 是否相等。

同时，在通分计算斜率是否相等时，中间值 dx}_0 \times \textit{dy}_1 与 dx}_1 \times \textit{dy}_0 有可能超过 32 位有符号整数的上界，因此我们可以考虑用 64 位整数保存中间值并进行判断。

代码

[sol1-C++]

class Solution {
public:
    int minimumLines(vector<vector<int>>& stockPrices) {
        sort(stockPrices.begin(), stockPrices.end());
        int n = stockPrices.size();
        if (n <= 2) {
            return n - 1;
        }
        int res = 1;
        for (int i = 2; i < n; ++i) {
            // 遍历相邻点对，并判断线段是否可以合并
            long long dx0 = stockPrices[i-1][0] - stockPrices[i-2][0];
            long long dy0 = stockPrices[i-1][1] - stockPrices[i-2][1];
            long long dx1 = stockPrices[i][0] - stockPrices[i-1][0];
            long long dy1 = stockPrices[i][1] - stockPrices[i-1][1];
            if (dx0 * dy1 != dy0 * dx1) {
                ++res;
            }
        }
        return res;
    }
};

[sol1-Python3]

class Solution:
    def minimumLines(self, stockPrices: List[List[int]]) -> int:
        stockPrices.sort()
        n = len(stockPrices)
        if n <= 2:
            return n - 1
        res = 1
        for i in range(2, n):
            # 遍历相邻点对，并判断线段是否可以合并
            dx0 = stockPrices[i-1][0] - stockPrices[i-2][0]
            dy0 = stockPrices[i-1][1] - stockPrices[i-2][1]
            dx1 = stockPrices[i][0] - stockPrices[i-1][0]
            dy1 = stockPrices[i][1] - stockPrices[i-1][1]
            if dx0 * dy1 != dy0 * dx1:
                res += 1
        return res

复杂度分析

• 时间复杂度：O(n \log n)，其中 n 为 stockPrices 的长度。即为对数组进行排序的时间复杂度。

• 空间复杂度：O(\log n)，即为排序的栈空间开销。