2285-道路的最大总重要性

给你一个整数 n ，表示一个国家里的城市数目。城市编号为 0 到 n - 1 。

给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条 双向
道路。

你需要给每个城市安排一个从 1 到 n 之间的整数值，且每个值只能被使用 一次 。道路的 重要性
定义为这条道路连接的两座城市数值 之和 。

请你返回在最优安排下， 所有道路重要性 之和 最大 为多少。

示例 1：

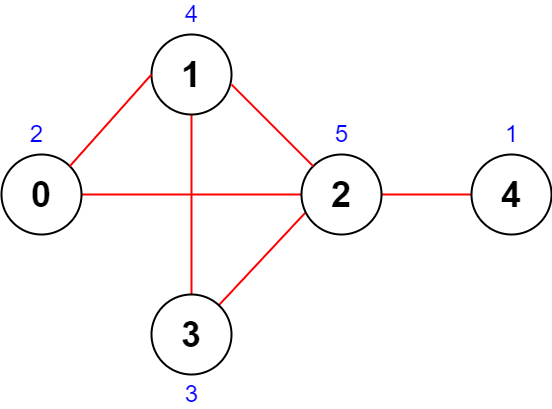
**输入：** n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
**输出：** 43
**解释：** 上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明，重要性之和不可能超过 43 。

示例 2：

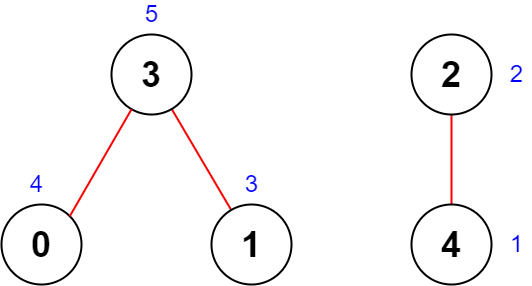
**输入：** n = 5, roads = [[0,3],[2,4],[1,3]]
**输出：** 20
**解释：** 上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明，重要性之和不可能超过 20 。

提示：

• 2 <= n <= 5 * 104
• 1 <= roads.length <= 5 * 104
• roads[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• 没有重复道路。

本题的 视频讲解 已出炉，欢迎三连~

---

设点 i 的度数（与点 i 相邻的城市数）为 deg}[i]，点 i 被安排的整数值为 p[i]，问题即最大化

\sum_{i=0}^{n-1} \textit{deg}[i]\cdot p[i]

根据 排序不等式 可知，deg 最小的安排 1，次小的安排 2，依此类推。因此排序后累加即得到答案。

[sol1-Python3]

class Solution:
    def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
        deg = [0] * n
        for x, y in roads:
            deg[x] += 1
            deg[y] += 1
        deg.sort()
        return sum(d * i for i, d in enumerate(deg, 1))

[sol1-Go]

func maximumImportance(n int, roads [][]int) (ans int64) {
	deg := make([]int, n)
	for _, r := range roads {
		deg[r[0]]++
		deg[r[1]]++
	}
	sort.Ints(deg)
	for i, d := range deg {
		ans += int64(d) * int64(i+1)
	}
	return
}