2290-到达角落需要移除障碍物的最小数目

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:07 2023-09-13 17:01:07 Updated    

给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n 。每个单元格都是两个值之一：

  • 0 表示一个 空 单元格，
  • 1 表示一个可以移除的 障碍物 。

你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。

现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ，返回需要移除的障碍物的 最小 数目。

示例 1：

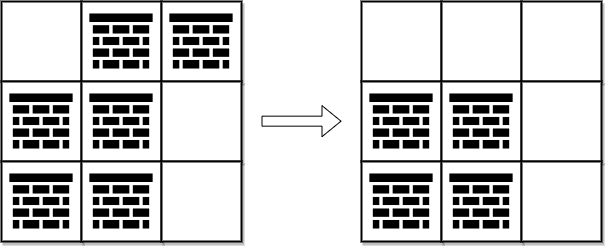
**输入：** grid = [[0,1,1],[1,1,0],[1,1,0]]
**输出：** 2
**解释：** 可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。
可以证明我们至少需要移除两个障碍物，所以返回 2 。
注意，可能存在其他方式来移除 2 个障碍物，创建出可行的路径。

示例 2：

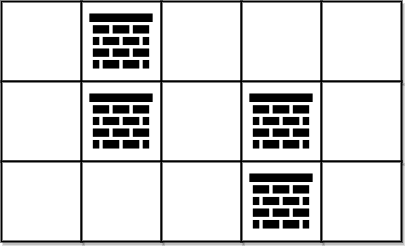
**输入：** grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
**输出：** 0
**解释：** 不移除任何障碍物就能从 (0, 0) 到 (2, 4) ，所以返回 0 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 105
  • 2 <= m * n <= 105
  • grid[i][j] 为 0 或 1
  • grid[0][0] == grid[m - 1][n - 1] == 0

本题 视频讲解 已出炉，包括 0-1 BFS 的原理，欢迎三连~

提示 1

把障碍物当作可以经过的单元格，经过它的代价为 1，空单元格经过的代价为 0。

提示 2

问题转化成从起点到终点的最短路。

提示 3

我们可以用 Dijkstra，但还可以用 0-1 BFS 来将时间复杂度优化至 O(mn)。

具体见 1368. 使网格图至少有一条有效路径的最小代价 官方题解的方法二，本文不再赘述。

复杂度分析

  • 时间复杂度：O(mn)。
  • 空间复杂度：O(mn)。
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def minimumObstacles(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dis = [[inf] * n for _ in range(m)]
        dis[0][0] = 0
        q = deque([(0, 0)])
        while q:
            x, y = q.popleft()
            for nx, ny in (x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1):
                if 0 <= nx < m and 0 <= ny < n:
                    g = grid[x][y]
                    if dis[x][y] + g < dis[nx][ny]:
                        dis[nx][ny] = dis[x][y] + g
                        if g == 0: q.appendleft((nx, ny))
                        else: q.append((nx, ny))
        return dis[m - 1][n - 1]
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    static final int[][] dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    public int minimumObstacles(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        var dis = new int[m][n];
        for (var i = 0; i < m; i++) Arrays.fill(dis[i], Integer.MAX_VALUE);
        dis[0][0] = 0;
        var q = new ArrayDeque<int[]>();
        q.addFirst(new int[]{0, 0});
        while (!q.isEmpty()) {
            var p = q.pollFirst();
            int x = p[0], y = p[1];
            for (var d : dirs) {
                int nx = x + d[0], ny = y + d[1];
                if (0 <= nx && nx < m && 0 <= ny && ny < n) {
                    var g = grid[nx][ny];
                    if (dis[x][y] + g < dis[nx][ny]) {
                        dis[nx][ny] = dis[x][y] + g;
                        if (g == 0) q.addFirst(new int[]{nx, ny});
                        else q.addLast(new int[]{nx, ny});
                    }
                }
            }
        }
        return dis[m - 1][n - 1];
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    static constexpr int dirs[4][2] = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };

public:
    int minimumObstacles(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        int dis[m][n];
        memset(dis, 0x3f, sizeof(dis));
        dis[0][0] = 0;
        deque<pair<int, int>> q;
        q.emplace_front(0, 0);
        while (!q.empty()) {
            auto [x, y] = q.front();
            q.pop_front();
            for (auto &[dx, dy] : dirs) {
                int nx = x + dx, ny = y + dy;
                if (0 <= nx && nx < m && 0 <= ny && ny < n) {
                    int g = grid[nx][ny];
                    if (dis[x][y] + g < dis[nx][ny]) {
                        dis[nx][ny] = dis[x][y] + g;
                        g == 0 ? q.emplace_front(nx, ny) : q.emplace_back(nx, ny);
                    }
                }
            }
        }
        return dis[m - 1][n - 1];
    }
};
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type pair struct{ x, y int }
var dir4 = []struct{ x, y int }{ {-1, 0}, {1, 0}, {0, -1}, {0, 1} }

func minimumObstacles(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	dis := make([][]int, m)
	for i := range dis {
		dis[i] = make([]int, n)
		for j := range dis[i] {
			dis[i][j] = m * n
		}
	}
	dis[0][0] = 0
	q := [2][]pair{ { {} }} // 两个 slice 头对头来实现 deque
	for len(q[0]) > 0 || len(q[1]) > 0 {
		var p pair
		if len(q[0]) > 0 {
			p, q[0] = q[0][len(q[0])-1], q[0][:len(q[0])-1]
		} else {
			p, q[1] = q[1][0], q[1][1:]
		}
		for _, d := range dir4 {
			x, y := p.x+d.x, p.y+d.y
			if 0 <= x && x < m && 0 <= y && y < n {
				g := grid[x][y]
				if dis[p.x][p.y]+g < dis[x][y] {
					dis[x][y] = dis[p.x][p.y] + g
					q[g] = append(q[g], pair{x, y})
				}
			}
		}
	}
	return dis[m-1][n-1]
}
 Comments
On this page
2290-到达角落需要移除障碍物的最小数目