2304-网格中的最小路径代价
给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1
的不同整数组成。你可以在此矩阵中,从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ,且满足 x < m - 1
,你可以移动到 (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1) **** 中的任何一个单元格。
注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为 (m * n) x n
,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid
最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发,返回到达
最后一行 任意单元格的最小路径代价 。
示例 1:
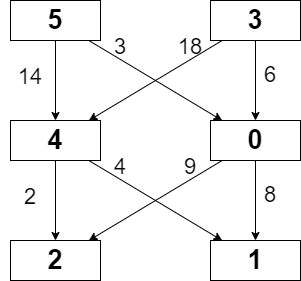
**输入:** grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
**输出:** 17
**解释:** 最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。
示例 2:
**输入:** grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
**输出:** 6
**解释:**
最小代价的路径是 2 -> 3 。
- 路径途经单元格值之和 2 + 3 = 5 。
- 从 2 移动到 3 的代价为 1 。
路径总代价为 5 + 1 = 6 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 50grid由从0到m * n - 1的不同整数组成moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
题目求什么就把状态定义成什么。
定义 f[i][j] 表示从第一行出发到达第 i 行第 j 列时的最小路径代价。
应该从哪些状态转移过来呢?
这里有一个技巧,就是考虑当前状态的「相邻」状态,或者说哪些状态可以「一步」到达当前状态。因为从更远的状态转移到当前状态,是必须要经过这些相邻的状态的,那么直接从这些相邻状态转移过来,就能算出正确的结果。
当你这样思考的时候,就会自然地想到从第 i-1 行转移过来了。
枚举从第 i-1 行的第 k 列转移过来,取最小值,则有
f[i][j] = \textit{grid}[i][j] + \min_{k=0}^{n-1} f[i-1][k] + \textit{moveCost}[\textit{grid}[i-1][k]][j]
答案为 \min(f[m-1])。
代码实现时可以用滚动数组优化。
1 | class Solution: |
1 | func minPathCost(grid [][]int, moveCost [][]int) int { |